之前,論智曾在TOP 10:初學者需要掌握的10大機器學習(ML)算法介紹了一些基礎算法及其思路,為了與該帖聯動,我們特從機器學習熱門課程HSE的Introduction to Deep Learning和吳恩達的Neural Networks and Deep Learning中挑選了一些題目,演示Python、TensorFlow和Keras在深度學習中的實戰應用.
如何建立一個線性分類器并進行優化.
在這個任務中,我們將實現一個線性分類器,并用numpy和隨機梯度下降算法對它進行訓練。
二元分類
為了更直觀,我們用人造數據(synthetic data)解決二元分類問題。
上圖中有紅、藍兩類數據,從分布上看它們不是線性可分的。所以為了分類,我們應該在里面添加特征或使用非線性模型。請注意,圖中兩類數據的決策邊緣都呈圓形,這意味著我們能通過建立二元特征來使它們線性分離,具體思路如下圖所示:
用expand函數添加二次函數后,我們得到了這樣的測試結果:
-
# 簡單的隨機數測試
-
dummy_X = np.array([
-
[0,0],
-
[1,0],
-
[2.61,-1.28],
-
[-0.59,2.1]
-
])
-
# 調用expand函數
-
dummy_expanded = expand(dummy_X)
-
# 它應該返回這些值: x0 x1 x0^2 x1^2 x0*x1 1
-
dummy_expanded_ans = np.array([[0. , 0. , 0. , 0. , 0. , 1. ],
-
[1. , 0. , 1. , 0. , 0. , 1. ],
-
[2.61, -1.28, 6.8121, 1.6384, -3.3408, 1. ],
-
[-0.59, 2.1 , 0.3481, 4.41, -1.239, 1. ]])
logistic回歸
曾經我們提到過,logistic回歸非常適合二元分類問題。為了分類對象,我們需要預測對象表示為1(默認類)的概率,這就需要用到線性模型和邏輯函數的輸出:
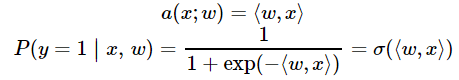
-
defprobability(X, w):
-
"""
-
對輸入賦值特征和權值
-
根據上式,返回輸入x后y==1的預測概率,P(y=1|x)
-
:參數 X: feature matrix X of shape [n_samples,6] (expanded) →特征矩陣X
-
:參數 w: weight vector w of shape [6] for each of the expanded features →權值向量w
-
:返回值: 范圍在 [0,1] 之間的一系列概率.
-
"""
-
return1./ (1+ np.exp(-np.dot(X, w)))
在logistic回歸中,我們能通過最小化交叉熵發現最優參數w:
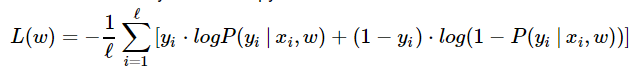
-
defcompute_loss(X, y, w):
-
"""
-
將特征矩陣X [n_samples,6], 目標向量 [n_samples] of 1/0,
-
以及權值向量 w [6]代入上述公式, 計算標量的損失函數.
-
"""
-
return-np.mean(y*np.log(probability(X, w)) + (1-y)*np.log(1-probability(X, w)))
由于用了梯度下降算法訓練模型,我們還需要計算梯度,具體來說,就是要對每個權值的損失函數求導:
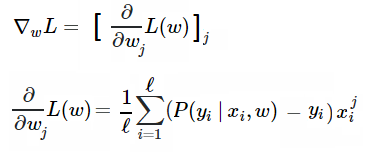
以下是具體的數學計算過程(也可點擊https://math.stackexchange.com/questions/477207/derivative-of-cost-function-for-logistic-regression/2539508#2539508查看):
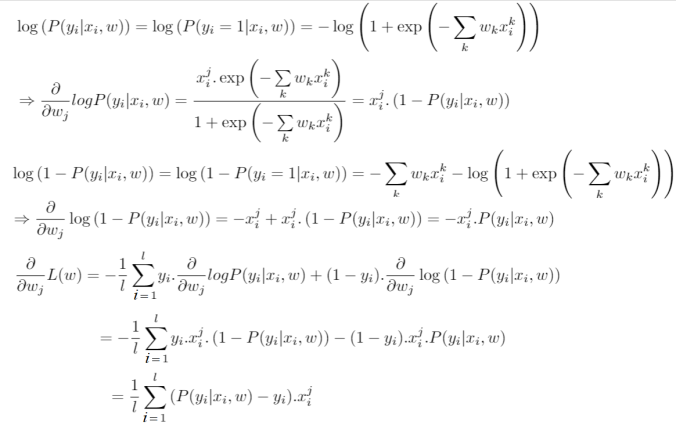
-
defcompute_grad(X, y, w):
-
"""
-
將特征矩陣X [n_samples,6], 目標向量 [n_samples] of 1/0,
-
以及權值向量 w [6]代入上述公式, 計算每個權值的導數vector [6].
-
"""
-
returnnp.dot((probability(X, w) - y), X) / X.shape[0]
訓練
現在我們已經建立了函數,接下來就該用隨機梯度下降訓練分類器了。我們將試著調試超參數,如batch size、學習率等,來獲得最佳設置。
Mini-batch SGD
不同于滿梯度下降,隨機梯度下降在每次迭代中只需要一個隨機樣本來計算其損失的梯度,并進入下一個步驟:
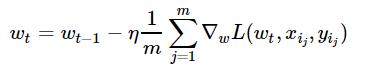
-
w = np.array([0,0,0,0,0,1])# 初始化
-
eta =0.05# 學習率
-
n_iter =100
-
batch_size =4
-
loss = np.zeros(n_iter)
-
foriinrange(n_iter):
-
ind = np.random.choice(X_expanded.shape[0], batch_size)
-
loss[i] = compute_loss(X_expanded, y, w)
-
dw = compute_grad(X_expanded[ind, :], y[ind], w)
-
w = w - eta*dw
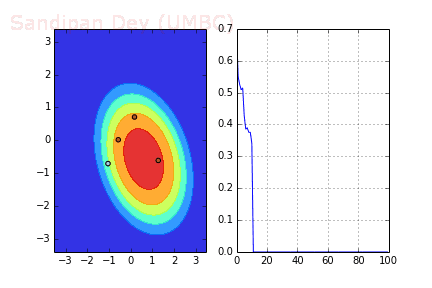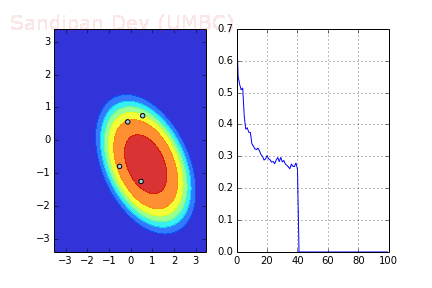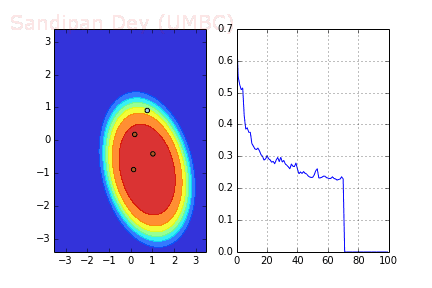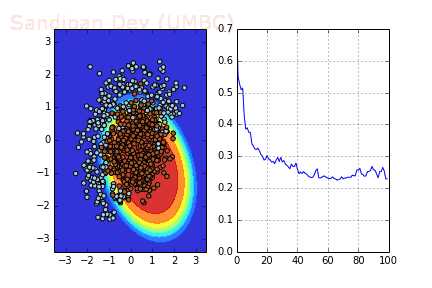
下圖展示了當batch size=4時,決策面(decision surface)和交叉熵損失函數如何隨著不同batch的SGD發生變化。
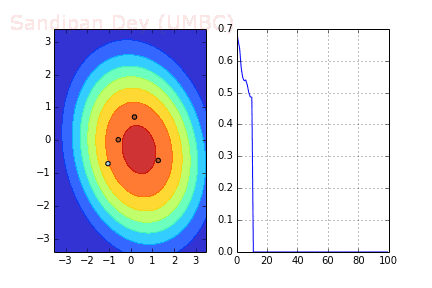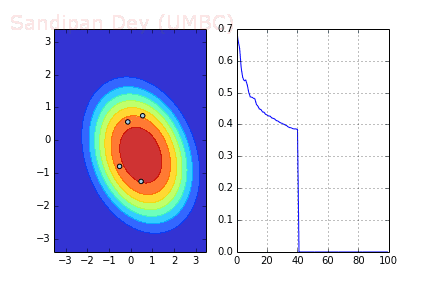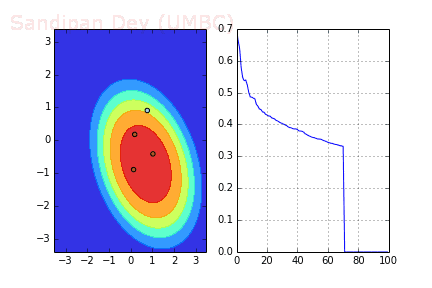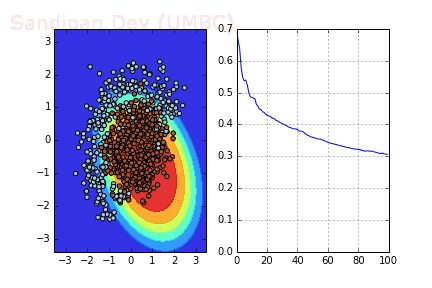
用Momentum優化SGD
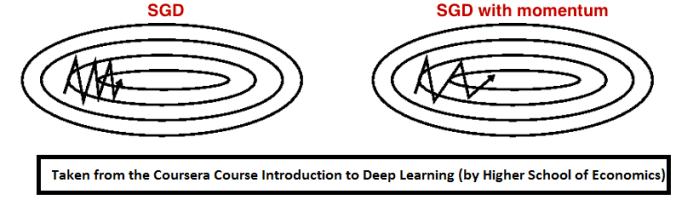
Momentum是模擬物理里動量的概念,如下圖所示,它能在相關方向加速SGD,抑制振蕩,從而加快收斂。從計算角度說,就是對上一步驟更新向量和當前更新向量做加權平均,將其用于當前計算。
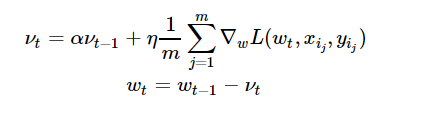
-
eta =0.05# 學習率
-
alpha =0.9# momentum
-
nu = np.zeros_like(w)
-
n_iter =100
-
batch_size =4
-
loss = np.zeros(n_iter)
-
foriinrange(n_iter):
-
ind = np.random.choice(X_expanded.shape[0], batch_size)
-
loss[i] = compute_loss(X_expanded, y, w)
-
dw = compute_grad(X_expanded[ind, :], y[ind], w)
-
nu = alpha*nu + eta*dw
-
w = w - nu
下圖展示了引入Momentum后,當batch size=4時相應決策面和交叉熵損失函數隨不同batch SGD+momentum發生的變化。可以看出,損失函數下降速度明顯加快,更快收斂。
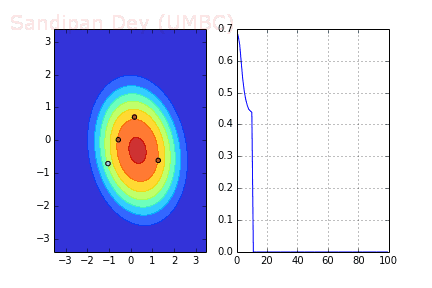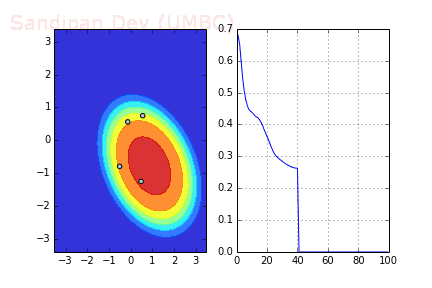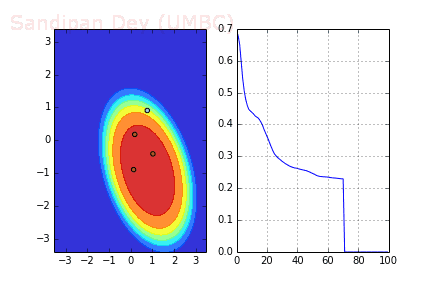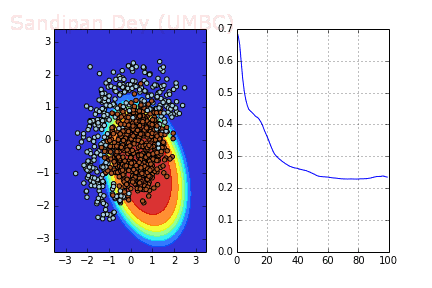
左:決策面;右:損失函數
RMSprop
加快收斂速度后,之后我們要做的是調整超參數學習率,這里我們介紹Hinton老爺子的RMSprop。這是一種十分高效的算法,利用梯度的平方來調整學習率:
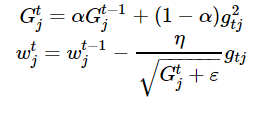
-
eta =0.05# 學習率
-
alpha =0.9# momentum
-
G = np.zeros_like(w)
-
eps =1e-8
-
n_iter =100
-
batch_size =4
-
loss = np.zeros(n_iter)
-
foriinrange(n_iter):
-
ind = np.random.choice(X_expanded.shape[0], batch_size)
-
loss[i] = compute_loss(X_expanded, y, w)
-
dw = compute_grad(X_expanded[ind, :], y[ind], w)
-
G = alpha*G + (1-alpha)*dw**2
-
w = w - eta*dw / np.sqrt(G + eps)
下圖是使用了SGD + RMSProp后決策面和損失函數的變化情況,較之之前,函數下降更快,收斂也更快。
-
ML
+關注
關注
0文章
149瀏覽量
34692 -
線性分類器
+關注
關注
0文章
3瀏覽量
1440
原文標題:課后作業(一):如何建立一個線性分類器并進行優化
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 實例:如何建立一個線性分類器并進行優化
實例:如何建立一個線性分類器并進行優化












評論