現實應用場景往往具有復雜的多變量交互作用和非線性行為,在數學上均屬于高階問題,存在于實際應用中的各個領域,如圖像處理中的去噪和超分辨率、工程設計與優化、金融工程中的期權定價和投資組合優化、醫療領域中的治療方案優化和藥物代謝過程等。
在現實應用中,解決高階問題充滿挑戰。一是容易陷入局部最優解。高階問題通常涉及大量變量和約束,導致解空間變得龐大和復雜,且存在多個局部最優解。因此,在尋找全局最優解的過程中,避免陷入局部最優解變得尤為關鍵,這增加了求解的難度。二是對計算資源需求高。這包括但不限于處理時間、內存容量和處理器性能。隨著變量數量的增加,求解所需的時間可能會以指數級增長,這不僅對硬件設施提出了更高的要求,也對算法的優化提出了挑戰。三是對解的精度要求高,小的誤差可能會導致解的質量顯著下降,最終影響結果的可靠性、有效性。
幸運的是,現實中的復雜應用場景通常是由最基礎的低階數學問題演化出來的。基礎的數學問題通過不斷組合和擴展,形成了復雜的應用場景。
比如,圖像處理是從像素操作(基礎矩陣運算)出發,發展出圖像濾波、邊緣檢測等基本圖像處理技術。在此基礎上,運用基礎卷積運算和激活函數,提取出圖像高層次特征,使其能夠處理復雜的圖像分類、目標檢測等任務,也構成了卷積神經網絡(CNN)的基本框架。進一步,集成學習和深度學習技術通過多層網絡結構和反向傳播算法,結合多個學習器,大幅提升了模型的處理能力和預測精度,最終形成強大的圖像處理與計算機視覺系統。
再舉一個簡單的例子,現實生活中的五顏六色,構成了豐富多彩的世界,但這么多階的復雜顏色分類,其實都可以歸結為最基礎的“紅黃藍”三原色。通過三原色的多種組合,才演化出更高階的、更細分的具象色彩。
由于高階問題很復雜,所以直接求解非常困難,但降階(二次化)可以將高階函數轉換為基礎的二次函數,從而簡化優化問題,使其更容易求解。
例如網絡安全問題中的RSA加密算法的破解,借助降階,用QUBO(二次無約束二值優化)可以建模整數分解問題,隨著量子比特的增加,用量子計算破解RSA算法將更容易。此外,銀行業務中通過設置信用評分卡的合理閾值,以使銀行的最終收入最多的復雜問題,也能利用QUBO建模進行求解,得到高收益的銀行卡設置方案。
面對不同行業場景下的實際問題的高階函數,基于玻色量子自研的開物SDK都可以實現輕松降階,將HOBO(高階二值優化)通過添加約束條件轉化為QUBO問題,簡化問題難度,大幅加快解決NP-Hard組合優化問題的速度。
降階思路:
HOBO可以通過添加約束條件轉化為QUBO問題。
具體來說,即通過變量替換,令y=x0x1,將原式中的單項式階數降低,并添加y=x0x1的約束。
銀行信用評分卡設置的降階案例
當大家借用充電寶的時候,都會顯示一個信用評分的免押金彈窗,這是我們能看得見的一種信用等級評分。當我們在申請銀行信用卡或相關的貸款等業務中,銀行對客戶授信之前,需要先通過各種審核規則對客戶的信用等級進行評定,通過評定后的客戶才能獲得信用或貸款資格,這是我們看不見的一種信用等級評分。
在銀行業,規則審核過程實際是經過一重或者多重組合規則后對客戶進行打分,這些規則就被稱為“信用評分卡”,每個信用評分卡又有多種閾值設置(有且只有一個閾值生效),這就使得不同的信用評分卡在不同的閾值下,對應不同的通過率和壞賬率,一般通過率越高,壞賬率也會越高,反之,通過率越低,壞賬率也越低。
對銀行來說,通過率越高,通過貸款資格審核的客戶數量就越多,相應的銀行獲得的利息收入就會越多,但高通過率一般對應著高壞賬率,而壞賬意味著資金的損失風險,因此銀行最終的收入可以定義為:
最終收入= 貸款利息收入-壞賬損失
我們將該問題進行做如下簡化:假設貸款資金為100萬元,銀行貸款利息收入率為8%,要為3種信用評分卡選取閾值。三種信用卡組合后,總通過率為所有信用卡的通過率相乘,壞賬率為三種評分卡對應壞賬率的平均值。也就是說,貸款利息收入=貸款資金×利息收入率×總通過率×(1-總壞賬率)
那么,如何設置合理的閾值,使得最終收入最多?
實際上使用QUBO建模可以進行求解,得到高收益的銀行卡設置方案。
設y1j,y2j,y3j分別代表信用卡的第1、2、3種信用評分卡選擇第j個閾值,選擇則取1,不選則取0,h1j,h2j,h3j分別是第1、2、3種信用評分卡選擇第j個閾值的壞賬率。那么最終的收益率可以表達為:
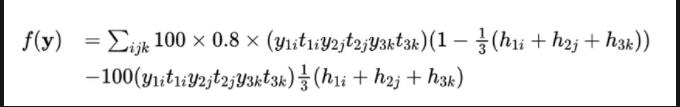
表達式中出現了高次項:y1iy2jy3k已經是三次項,需要借助降階把它變成二次項。
設置輔助變量qij,用它替換公式中的y1iy2j并約束qij=y1iy2j。 借助新增的輔助變量和約束,原問題就轉化為了二次問題。而要使得約束成立的方式是在原式中添加懲罰項,即Rosenberg二次懲罰項:
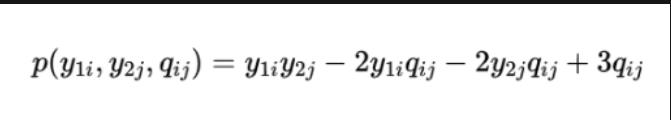
最終新的多項式為
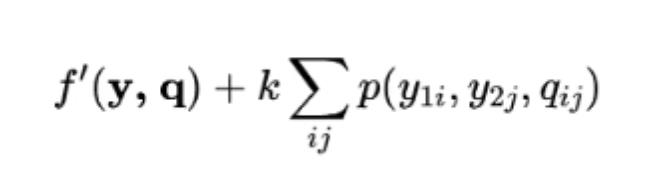
其中k是懲罰項系數。
其它降階方法
對于特定的情況,也存在一些特殊的降階方法。
如當某一高次項的系數為負數時,可以使用不同的二次化方法:
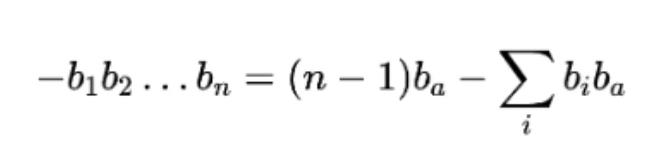
其中ba是輔助變量。
當b1b2...bn=1時,說明對所有的都滿足bi=1,由于ba的取值只受b1,b2...bn影響,所以容易驗證當ba取1時等式右側QUBO值更低。當等式右側取最低值時正好與等式左側相等,取值為-1。
當b1b2...bn=0時,說明存在bi都滿足bi=0,ba取1代入等式右側得到
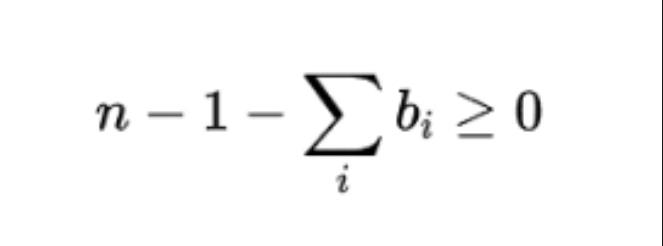
所以容易驗證當ba取0時等式右側QUBO值更低。當等式右側取最低值時正好與等式左側相等,取值為0。
舉例:
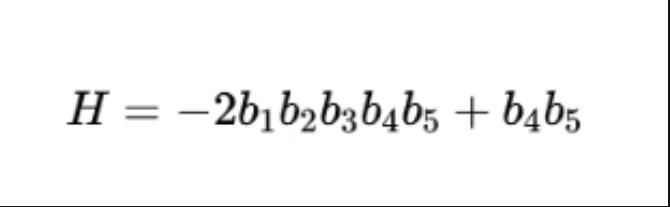
可以等價替換為:
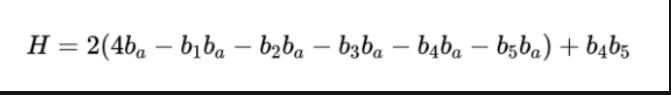
相比于上述方法,該方法可以用一個輔助變量將1個n次項變為2次,只增加1個輔助變量。但是應用范圍要小。
針對不同的應用場景,還存在一些其它特定的降階方法。
總結
對于現實生活中的不同行業不同場景下的復雜問題,高階函數的降階求解是一種通用型求解思維,基于玻色量子自研的開物SDK,用戶只需關注建立與場景所對應的數學模型,SDK提供的方法可以自動完成降階,用戶不用關心背后的復雜度,大大降低用戶使用相干光量子計算機求解問題的難度。
-
函數
+關注
關注
3文章
4344瀏覽量
62855 -
SDK
+關注
關注
3文章
1044瀏覽量
46121 -
量子計算
+關注
關注
4文章
1108瀏覽量
35001 -
光量子計算機
+關注
關注
0文章
10瀏覽量
1674 -
玻色量子
+關注
關注
0文章
50瀏覽量
528
原文標題:量子計算場景實用秘籍:開物SDK之“高階函數降階”
文章出處:【微信號:玻色量子,微信公眾號:玻色量子】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 量子計算場景實用秘籍:開物SDK之“高階函數降階”
量子計算場景實用秘籍:開物SDK之“高階函數降階”
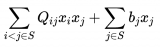











評論