在各行業應用場景的數學模型構建中,經常會遇到實際問題的計算規模巨大,模型所包含的變量數超出現有量子計算機比特數的情況,導致無法直接使用量子計算機進行求解,而是先要對原問題進行拆分,這時就需要一種稱為“subQUBO算法”的幫助。
subQUBO算法是一種將大規模組合優化問題分解為若干個小規模問題以便能在當前中小規模量子計算機上實現求解的方法。它的核心思想是通過軟件手段將原問題拆解,并融合經典和量子兩種模型,重構成一種“量子計算+經典計算”混合架構的全新數學模型,從而使得現有的光量子計算機能夠直接處理,同時,該算法可以確保被分解后的小問題集合在求解質量上,仍舊與原有大問題是完全一致的。這項非常實用的模型預處理功能,也是玻色量子發布的開物SDK強大能力之一。
subQUBO算法的應用場景主要集中在解決大規模優化問題中,尤其是在受到當前量子計算機比特數限制而難以直接求解的問題上。例如,生物制藥領域的藥物發現和網絡科學領域的社區發現兩大典型場景案例。
藥物發現場景
藥物發現作為生物制藥領域的核心環節,致力于尋找對特定疾病具有療效的潛在藥物分子,包括了靶標鑒定、藥物設計,合成、評價等多個步驟。其中,分子對接作為藥物發現早期虛擬篩選、藥物設計的重要技術手段之一,多被用于預測和分析配體(小分子化合物)與受體(蛋白質或核酸)之間的結合過程。
通過計算配體受體之間的空間互補以及能量匹配來尋找其最佳的復合物模式。我們將分子對接過程中的構象采樣問題轉化為配體原子和受體結合口袋的空間格點匹配問題,通過構建QUBO模型可以在相干光量子計算機上實現求解,再將求得的解轉換為空間位置以最終獲得復合物pose信息,從而加速了分子對接的計算過程,并且還能有效的提高分子對接的規模和質量。
但是,當配體和受體的分子量較大時,或是可選的受體結合口袋較多時,原有的QUBO模型所包含的變量數也會隨之增加,這就對量子計算機的比特規模提出了更高的要求。這時我們通過subQUBO方法就可以從原QUBO問題中抽取出部分變量形成若干子問題,并通過迭代更新來優化求解過程,使得分解后的問題求解結果能夠不斷逼近最優解。
社區發現場景
網絡科學是利用數學理論研究數據網絡的學科,重點在于分析和表征網絡行為。現實世界網絡的一個重要特征是它們具有社區結構,這可以通過圖方法來實現建模。識別社區結構是理解不同網絡結構的重要手段,在社交網絡、金融風控、生命科學等領域都有巨大應用價值。
尤其在大規模網絡中,檢測社區結構更加有價值,有許多應用產品都是使用社區檢測算法來揭示網絡中的隱藏信息。例如,在社交網絡中找到具有相似行為的用戶,通過他們的購物習慣對電子商務中的客戶進行分類能夠有效提升營銷成功率。同樣,社區檢測在設計延遲容忍網絡中的網絡協議和在線社交網絡中的蠕蟲遏制中能夠發揮重要作用。在數據網絡中,識別惡意用戶社區是很有幫助的。在智能營銷中社區發現具有一些有趣的應用,例如增強在線購物者、產品推薦和定向廣告。在大型購物網絡中,社區檢測可以用于分類客戶并根據他們的購買歷史提供未來購買的建議。
社區檢測算法的性能在很大程度上取決于網絡的拓撲結構,網絡可以是靜態的或動態的。模塊度最大化和譜聚類分別被認為是靜態網絡中社區識別的主要方法。我們將傳統的基于模塊度的社區發現模型轉化為QUBO形式,并使用玻色量子的相干光量子計算機實現了求解。而往往在實際場景中,在線網絡用戶數或者生命科學領域的細胞數量非常龐大,所涉及的計算規模都會超過現有量子比特數量的限制,那么我們就可以借助subQUBO算法算法,進行問題拆分,最終完成求解。
QUBO問題的分解 一個較大的QUBO優化問題,在固定一部分變量的取值后,可以形成一個更小的QUBO優化問題。
令原始的QUBO問題為:
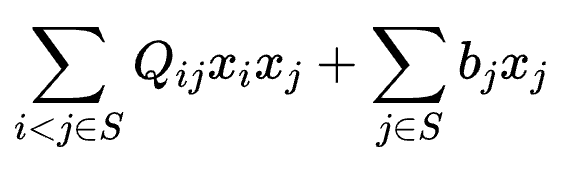
令可活動變量下標集合為Sf。令固定的變量下標集合為Sc=SSf,取值為
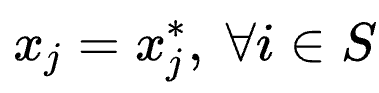
如此,原始的QUBO問題可改寫為以xi∈Sf為變量的問題:
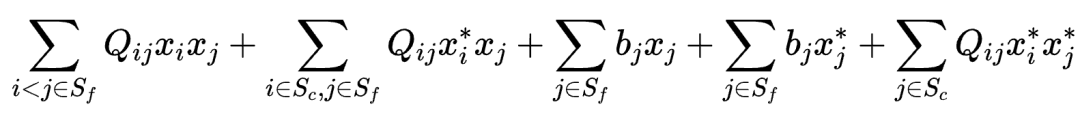
其中,二次項為:
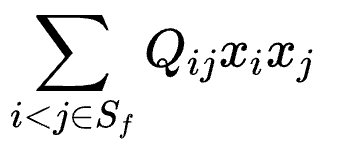
一次項為:
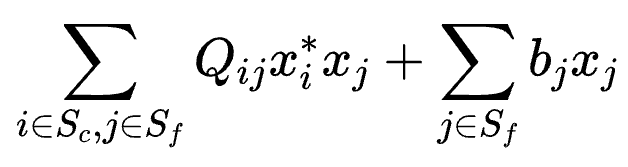
常數項為:
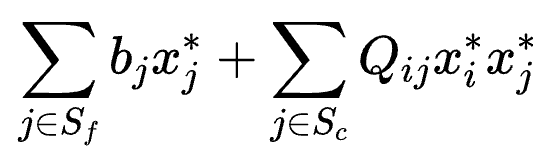
忽略常數項,則有:
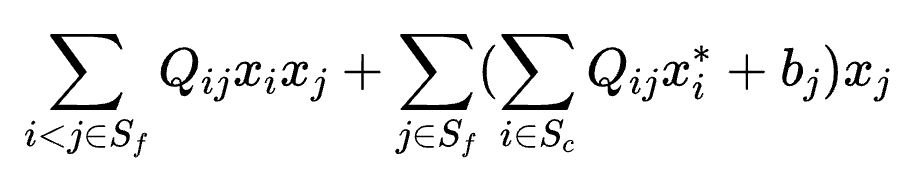
相干光量子計算機直接求解的Ising模型和QUBO模型是等價的,在實現時直接對Ising模型抽取子問題也可以達到同樣的作用。優化過程:

如偽代碼所示,通過subqubo優化時,首先要確定初始解向量,之后的求解過程不斷更新解向量。之后的迭代過程中,需要執行的操作包括子問題變量集合的選取,子問題的求解與更新答案,全局優化。
子問題變量集合的選取:
變量集合的選取有很多不同的策略,策略的選取取決于實際問題。選取的策略包括:
(1)將QUBO問題看成一張圖,根據圖的連通性選擇子問題
(2)有限選擇重要的或者當前不確定程度更高的變量
(3)根據實際問題的結構選擇,如選擇在實際問題中相關的變量
子問題的求解與更新答案:
參考前一節問題的分解,我們在選取變量集合之后就可以用原問題和當前的解生成新的子問題。子問題的變量就是我們所選的變量集合。求解子問題之后,將變量的改變在原問題的解中做相應的更新。有時subQUBO算法會維護一個解集合,這只需將新產生的解加入到解集合中并對維護的解集作相應更新。
全局優化
每次優化都只考慮使用同一標準選取的一部分變量,有時候可能會導致算法錯過一些變量。通過禁忌搜索,模擬退火等算法,引入不同的優化方式,可以幫助跳出局部最優。
子問題如何選取?
本節以選擇不確定程度更高的變量為例,講解子問題的選取過程。
當被固定的變量都已經得到最優解,那么subQUBO表達式的最優解與QUBO表達式的最優解相同。因此,合理的方式應該是將有更高概率已經獲得正確解的變量固定,subQUBO表達式選取難以確定最優解的變量。
于是,該方法通過之前求解時獲得的解來判斷每個變量當前的解有多大信心為正確解,結果多數為1則為1,多數為0則為0,1和0的次數差不多說明難以確定。具體操作為通過 |解為1的次數-求解次數/2| 來判斷。
當該值較大時,變量有較高信心為1或0的某一個值,反之則說明難以判斷該變量的值應該為1或0,應該優先加入subQUBO。
總結
現實中的問題普遍存在大規模求解的情況,subQUBO算法為用戶提供了一種全新的解決思路,并證明其是一種用于解決大規模QUBO問題的有效方法。它通過將原始問題分解為多個子問題,并在迭代過程中優化這些子問題的求解效果,從而逐步逼近全局最優解。
在藥物發現和社區發現等實際應用中,subQUBO算法能夠處理超出量子計算機比特數限制的問題,提高了量子計算能夠覆蓋到的問題規模。并且子問題的選取策略也是多樣的,可根據實際問題特點選擇合適的變量集合。
顯然,通過結合經典算法和量子計算,subQUBO算法為解決復雜優化問題提供了新的思路和方法。基于玻色量子自研的開物SDK,用戶只需關注建立與場景所對應的數學模型,SDK提供的方法可以自動完成問題分解,用戶無需擔心其背后的復雜度,這將極大的降低用戶使用相干光量子計算機求解實際問題的難度。
文章來源 :玻色量子 在此特別鳴謝!
-
算法
+關注
關注
23文章
4681瀏覽量
94326 -
SDK
+關注
關注
3文章
1057瀏覽量
47298 -
量子計算
+關注
關注
4文章
1130瀏覽量
35446 -
玻色量子
+關注
關注
0文章
56瀏覽量
637
原文標題:量子計算場景實用秘籍:開物SDK之subQUBO算法分解
文章出處:【微信號:玻色量子,微信公眾號:玻色量子】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
量子計算場景實用秘籍:開物SDK之“高階函數降階”




















評論