摘 要
隨著高中物理新教材的使用以及新高考在全國的陸續(xù)施行,對高中物理教學(xué)而言,無論是教學(xué)內(nèi)容還是教學(xué)形式都出現(xiàn)了許多新的課題。這就使得站在高觀點下(即大學(xué)普通物理學(xué)角度)研究高中物理,不僅成為教學(xué)改革的迫切任務(wù),也成為了新課程下物理教學(xué)改革的一個主流方向。
本文將以 2020 年高考全國甲卷第 21 題和 2020 年高考全國乙卷第 20 題為例,從大學(xué)電磁學(xué)視角分析高考電磁學(xué)的問題,旨在引導(dǎo)物理專業(yè)的師范生要認(rèn)真學(xué)好專業(yè)課程,提高自身的物理素養(yǎng),能站在高觀點下審視高中物理的內(nèi)容,解決教學(xué)中的疑難問題。另外,希望中學(xué)的一線教師,要終身學(xué)習(xí),不斷重溫大學(xué)的物理課程,站在高觀點下審視高中物理的內(nèi)容,不斷解決教學(xué)中的疑難問題,使自己的教學(xué)更具有針對性和創(chuàng)造性,不斷地提高教育教學(xué)水平,向更高的層次邁進(jìn),促進(jìn)學(xué)生核心素養(yǎng)的全面提升。
問題一 電磁滑桿問題
在研究電磁滑桿問題時,高中階段所求解的內(nèi)容往往是時間趨于無窮時的極限情況,即金屬桿的最后狀態(tài)。教師往往忽略了對中間過程的分析,忽視了對學(xué)生極限思維的培養(yǎng)。下面我們以 2020 年全國甲卷第 21 題為例,運(yùn)用高等數(shù)學(xué)手段對金屬框、導(dǎo)體棒運(yùn)動情況的變化作全程分析。原題如下:
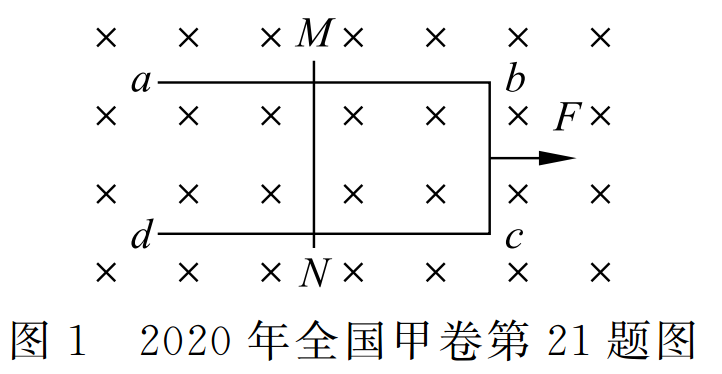
如圖 1 所示,U 形光滑金屬框abcd置于水平絕緣平臺上,ab和dc邊平行,和bc邊垂直。ab、dc足夠長,整個金屬框電阻可忽略。一根具有一定電阻的導(dǎo)體棒MN置于金屬框上,用水平恒力F向右拉動金屬框,運(yùn)動過程中,裝置始終處于豎直向下的勻強(qiáng)磁場中,MN與金屬框保持良好接觸,且與bc邊保持平行。經(jīng)過一段時間后
A.金屬框的速度大小趨于恒定值
B.金屬框的加速度大小趨于恒定值
C.導(dǎo)體棒所受安培力的大小趨于恒定值
D.導(dǎo)體棒到金屬框bc邊的距離趨于恒定值
定性分析:設(shè)bc邊的長度為l,導(dǎo)體棒的電阻為R。設(shè)金屬框、導(dǎo)體棒的質(zhì)量分別為m1、m2,某時刻的速度分別為v1、v2,加速度分別為a1、a2。對金屬框、導(dǎo)體棒,根據(jù)牛頓第二定律,有
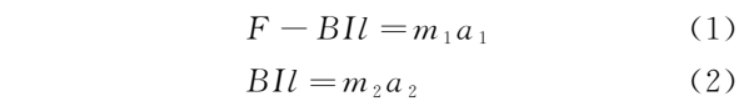
感應(yīng)電流為
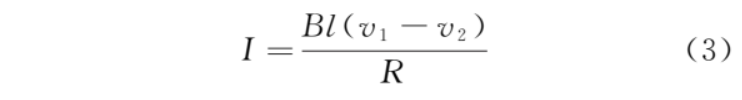
感應(yīng)電流從 0 開始增大,則a1從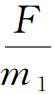 開始減小,a2?從 0 開始增大,加速度差為
開始減小,a2?從 0 開始增大,加速度差為
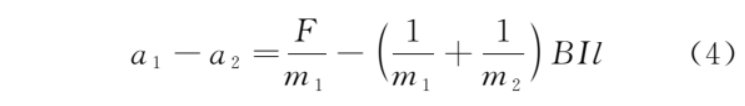
感應(yīng)電流從 0 開始增大,則加速度差減小,當(dāng)差值等于 0 時,由式 (1) 和式 (2),得
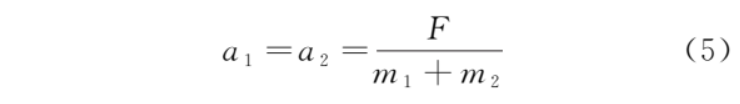
由式 (3) 和式 (4),得
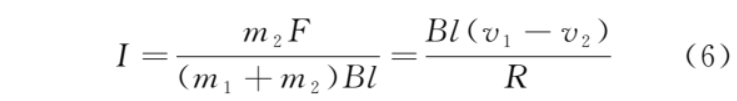
從而速度差為
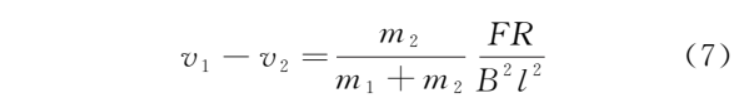
此后金屬框與導(dǎo)體棒的速度差維持不變,感應(yīng)電流不變,導(dǎo)體棒受到的安培力不變,加速度不變。A 選項錯誤,B、C 選項正確。金屬框與導(dǎo)體棒的速度差不變,但導(dǎo)體棒的速度小于金屬框的速度,導(dǎo)體棒到金屬框bc邊的距離越來越大,D 選項錯誤。
高中階段用定性分析解釋,大部分學(xué)生是可以理解和接受的,但是從定量的角度似乎更有“說服力”,雖然定量計算超出了高中知識范圍,不過作為教師,我們不僅要知其然,更要知其所以然。下面我們做定量研究,以起拋磚引玉之效。
定量研究:以金屬框、導(dǎo)體棒組成的系統(tǒng)為研究對象,根據(jù)動量定理,有
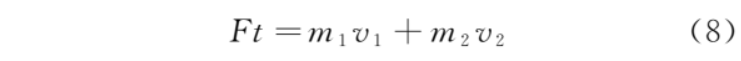
則
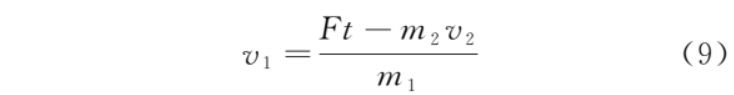
兩桿所受安培力大小均為
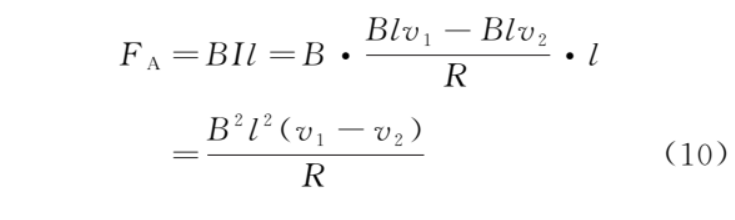
對導(dǎo)體棒,根據(jù)牛頓第二定律,有
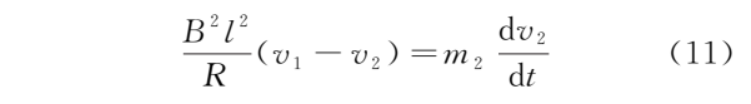
由式 (9) 和式 (11) 得關(guān)于 v2 的微分方程
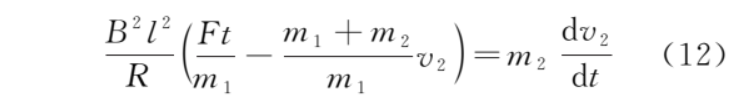
初始條件為
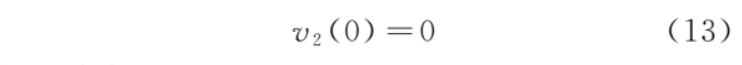
解微分方程,得
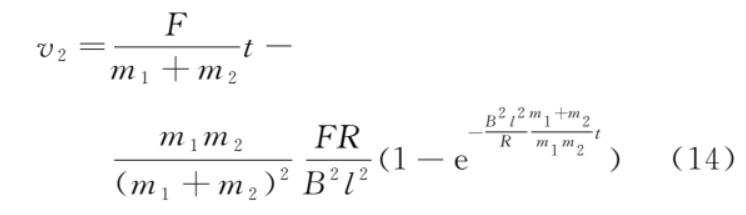
所以
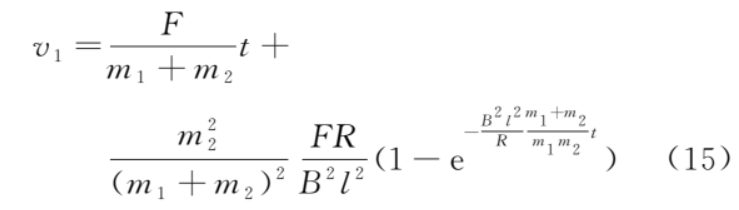
加速度
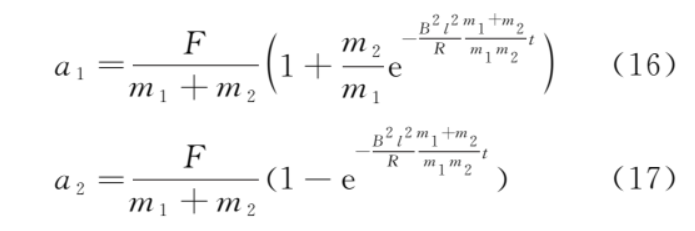
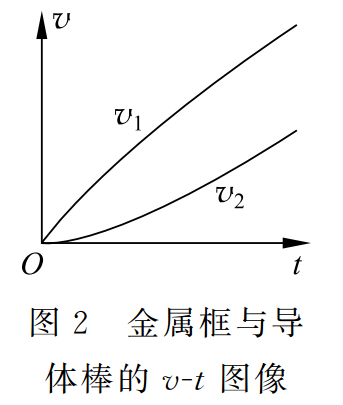
從式 (16) 和式 (17) 我們可以看出,金屬框做加速度減小的加速運(yùn)動,導(dǎo)體棒做加速度增大的加速運(yùn)動。當(dāng)時間t→∞時,a1和a2趨于穩(wěn)態(tài)值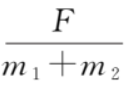 。金屬框、導(dǎo)體棒的?v-t?圖像如圖 2 所示,由式 (14) 和式 (15),可得速度差為
。金屬框、導(dǎo)體棒的?v-t?圖像如圖 2 所示,由式 (14) 和式 (15),可得速度差為
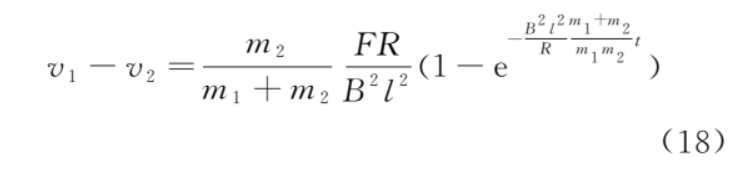
當(dāng)時間t→∞時,速度差趨于穩(wěn)態(tài)值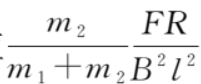 。
。
問題二 帶電圓環(huán)的電場強(qiáng)度問題
2020 年高考全國乙卷第 20 題以均勻帶電圓環(huán)為背景,不僅考查了靜電場中電場強(qiáng)度和電勢的疊加,而且也考查了核心素養(yǎng)中的物質(zhì)觀念、模型構(gòu)建、科學(xué)推理和科學(xué)論證。原題如下:
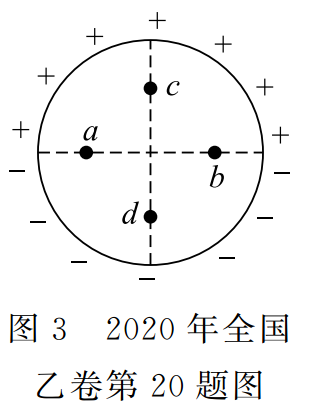
如圖 3 所示,豎直面內(nèi)一絕緣細(xì)圓環(huán)的上、下半圓分別均勻分布著等量異種電荷。a、b為圓環(huán)水平直徑上的兩個點,c、d為豎直直徑上的兩個點,它們與圓心的距離均相等。則
A.a(chǎn)、b兩點的場強(qiáng)相等
B.a(chǎn)、b兩點的電勢相等
C.c、d兩點的場強(qiáng)相等
D.c、d兩點的電勢相等
下面運(yùn)用大學(xué)電磁學(xué)知識,對a、b、c、d四點的電場強(qiáng)度作定量研究。
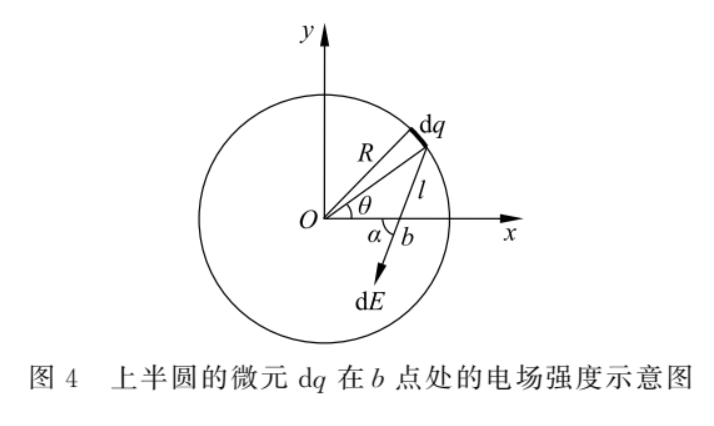
如圖 4 所示,設(shè)細(xì)圓環(huán)的半徑為R,電荷線密度為λ,b點距圓心O為r(r
根據(jù)余弦定理,有
上半圓的微元 dq 在 b 點的電場強(qiáng)度為
電場強(qiáng)度平行于y軸的分量為
從而
根據(jù)對稱性,上、下半圓對稱位置的微元dq在b點產(chǎn)生的電場平行于x軸的分量等值反向,所以b點的電場強(qiáng)度為
同理可得a、c、d三點的電場強(qiáng)度。
若上、下半圓帶等量同種正電荷,a、b、c、d四點的電場強(qiáng)度又該如何呢?在實際求解中,要用到一類特殊的積分——橢圓積分。橢圓積分是一種特殊函數(shù)的積分,不能用普通的積分方法來求解。它只能用二項式定理展開,得出一個收斂級數(shù),并逐項加以積分,至于取項數(shù)的多少,視結(jié)果的精度需要而定。常用的全橢圓積分有三類,它們的解分別是
1) 第一類全橢圓積分
2) 第二類全橢圓積分
3) 第三類全橢圓積分
它不能寫成冪級數(shù)的形式。下面我們來作具體的分析。
根據(jù)對稱性,上、下半圓對稱位置的微元dq在b點產(chǎn)生的電場平行于y軸的分量等值反向,故
從而
其中
令θ=π+2φ,并且利用式 (25) 和式 (27)則
其中,
除此以外,還有一些類似的高考題需要探討。盡管在高中階段我們不要求學(xué)生作上述的定量研究,但作為一名優(yōu)秀的物理教師,在給學(xué)生一碗水的同時,自己得有一桶水。所以我們對一道試題既要有讓學(xué)生理解并掌握的定性分析,還要有能讓自己信服的定量研究。只有處理好定性與定量的關(guān)系,站在高觀點下看問題,才能對問題的認(rèn)識更加深入透徹,講解得更加得心應(yīng)手。
審核編輯:黃飛
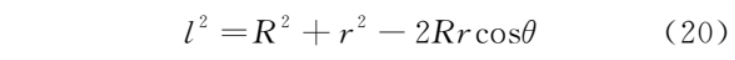
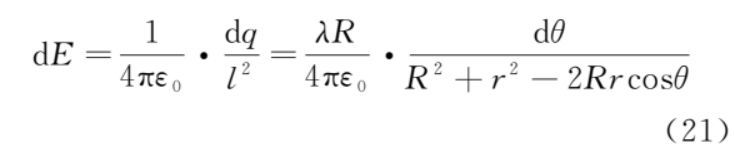
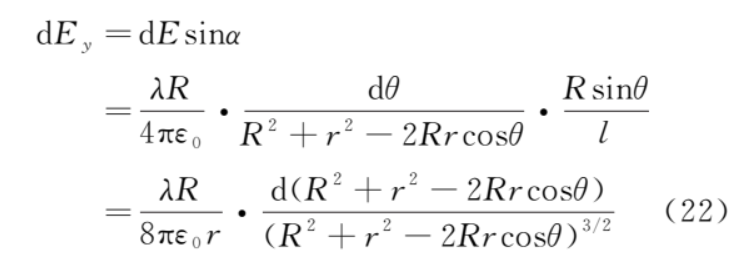
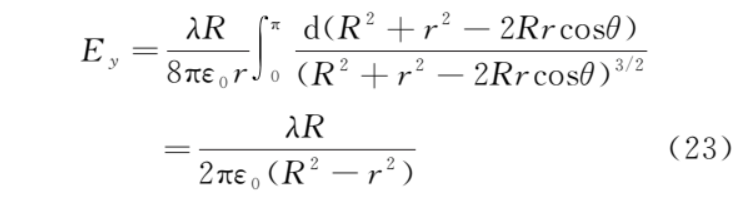
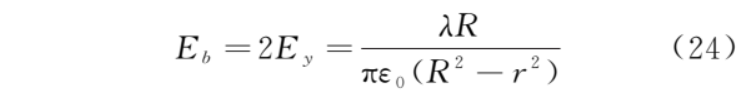
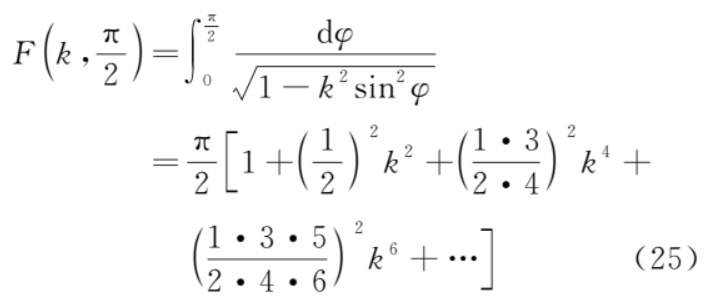
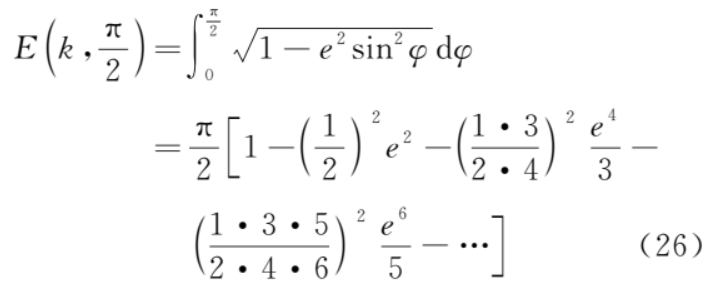
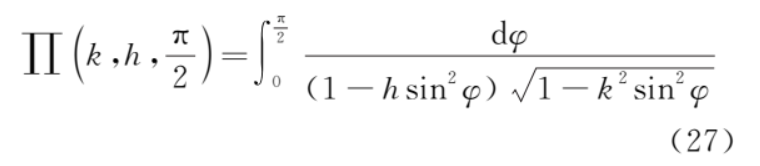
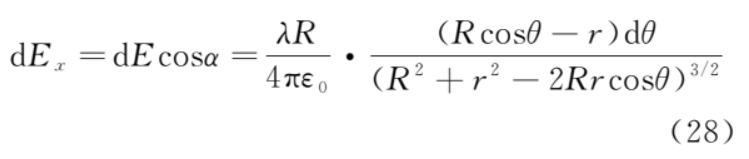
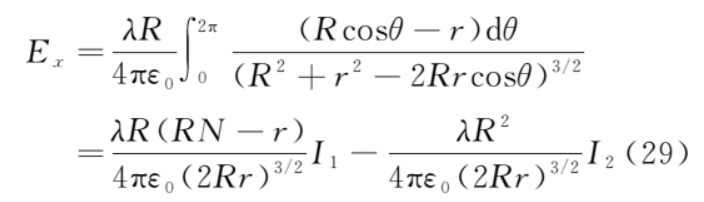
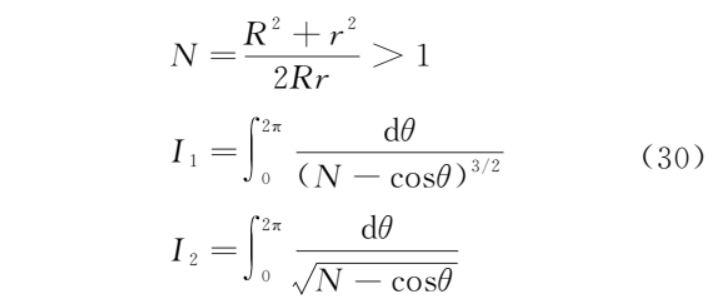
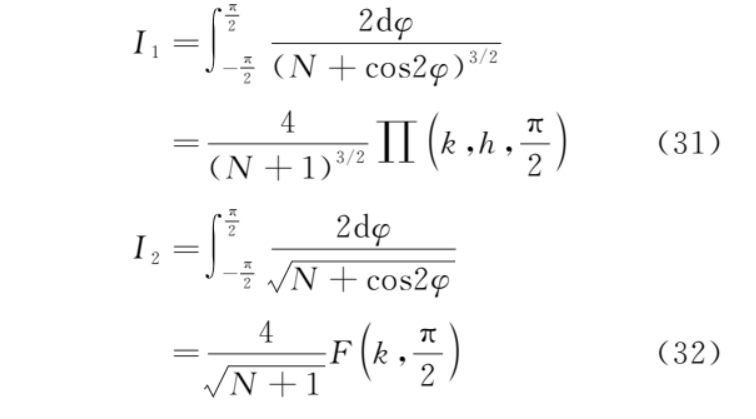
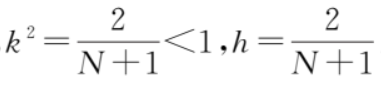 。
。
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4344瀏覽量
62864 -
電磁學(xué)
+關(guān)注
關(guān)注
1文章
108瀏覽量
14218 -
電場強(qiáng)度
+關(guān)注
關(guān)注
0文章
12瀏覽量
7410 -
感應(yīng)電流
+關(guān)注
關(guān)注
0文章
88瀏覽量
11952
原文標(biāo)題:大學(xué)電磁學(xué)視角下的高考電磁學(xué)問題研究
文章出處:【微信號:EMC_EMI,微信公眾號:電磁兼容EMC】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
計算電磁學(xué)的幾種方法的區(qū)別介紹
電磁學(xué)發(fā)展史介紹
電磁學(xué)理論的建立
計算電磁學(xué)基礎(chǔ)知識總結(jié)
深入研究徹底掌握設(shè)備樹
電磁學(xué)的數(shù)學(xué)基礎(chǔ)
電磁學(xué)課件練習(xí)題 (電磁學(xué)習(xí)題集解答)
電磁場理論與計算電磁學(xué)的學(xué)習(xí)課件免費(fèi)下載
電磁學(xué)的發(fā)展歷史詳細(xì)概述





 深入研究高考電磁學(xué)問題研究
深入研究高考電磁學(xué)問題研究










評論