關鍵點:
直方圖測試是確定模數轉換器(ADC)靜態參數的最流行方法之一。
直方圖測試使用統計分析來確定ADC的過渡點,而不是直接測量過渡點。
線性斜坡直方圖測試方法可以用于測量ADC的微分非線性度(DNL)誤差。
摘要:
直方圖測試是測試ADC靜態參數的最受歡迎的方法之一。該方法通過分析ADC輸出的統計數據來確定過渡點,能夠在給定的測量時間內實現接近理論最優精度。與傳統的伺服環測試方法相比,直方圖測試方法對于高噪聲水平下的ADC具有更好的效率。線性斜坡直方圖測試是一種常用的直方圖測試方法,可以用于測量ADC的微分非線性度(DNL)誤差。該方法使用線性斜坡輸入信號,并通過統計ADC輸出來計算過渡點的寬度。除了DNL誤差測量之外,直方圖測試還可以用于測量ADC的整體非線性度(INL),但由于測量誤差的累積和輸入信號非線性度的限制,INL的測量更加困難。
直方圖測試是確定模數轉換器 (ADC) 靜態參數的最流行的方法。在本文中,了解直方圖測試的基礎知識以及如何使用線性斜坡直方圖測試的細節。
靜態線性測試對于模數轉換器 (ADC) 制造的經濟性非常重要,這就是為什么學術界和工業界的研究人員投入大量工作來開發更高效的 ADC 測試方法。
本系列的上一篇文章介紹了用于測試 ADC 靜態參數的伺服環路方法。在本期中,我們將總體討論直方圖方法,并特別探討線性斜坡直方圖測試的用途。
不過,首先讓我們看一下伺服環方法的主要缺點,正是這些缺點使得開發這種替代測試方法成為必要。
伺服環路方法:ADC 噪聲影響
雖然伺服環路方法是一種流行的工業測試技術,但它無法為具有較大輸入參考噪聲的 ADC 提供最佳效率。它在給定測量時間內的精度明顯低于代表理論最佳精度的 Cramér-Rao 界限。圖 1 比較了伺服環路測試的性能(表示為“傳統”圖)與 Cramér-Rao 界限預測的精度。
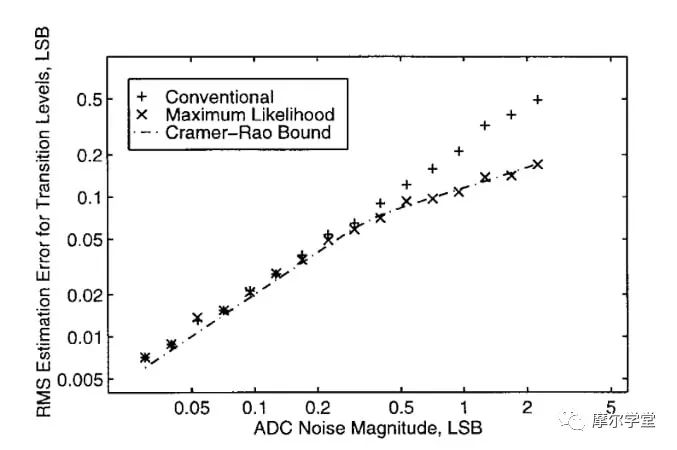
*圖 1.*伺服環路測試性能精度與理論最佳值的比較。圖片由P. Capofreddi提供
正如您所看到的,伺服環路方法無法在較高噪聲水平下提供最佳效率。
對于輸入參考噪聲足夠低的 14 位 ADC,伺服環路方法可能會令人滿意地工作。然而,當今許多高分辨率 ADC 都具有高輸入帶寬,導致峰峰值、輸入參考噪聲超過 2 LSB(最低有效位)。這就是為什么我們需要能夠導出 ADC 傳輸函數(無論其噪聲水平如何)的測試方法。
ADC 的直方圖測試
直方圖測試也稱為代碼密度測試,是迄今為止測試 ADC 靜態參數最流行的方法。通過該方法在給定測量時間內實現的精度非常接近 Cramér-Rao 界限指定的理論最佳值(圖 2)。
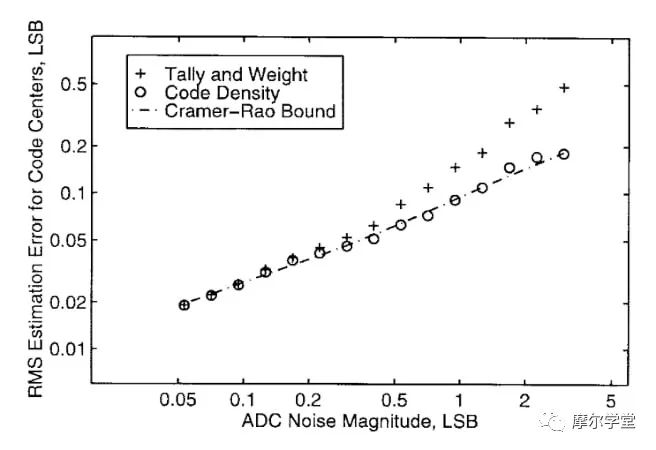
*圖 2.*與理論最佳值相比的直方圖測試性能精度。圖片由P. Capofreddi提供
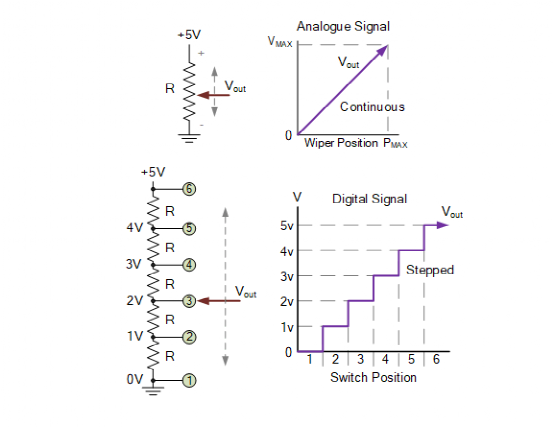
與直接測量 ADC 轉變點的伺服環路方法不同,直方圖方法使用轉換器輸出的統計分析來確定轉變點。圖 3 說明了直方圖測試背后的基本思想。
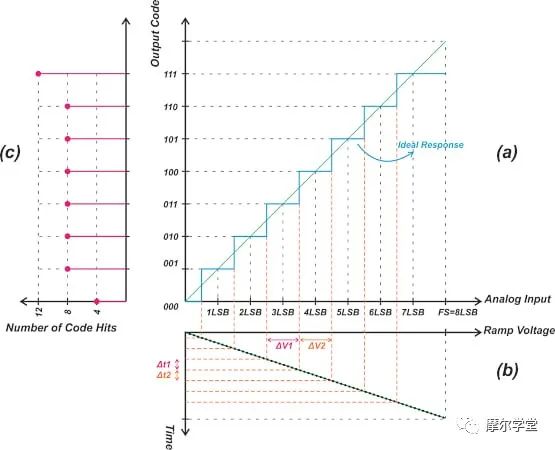
*圖 3.*從右上角順時針方向 — 理想 3 位 ADC 的傳輸特性、應用于 ADC 輸入的滿量程斜坡的旋轉波形以及該波形的旋轉直方圖。圖片由 Steve Arar 提供
圖 3 可分為三個圖,上面用字母表示。圖 3(a) 顯示了理想 3 位 ADC 的傳輸特性。圖 3(b) 顯示了應用于 ADC 輸入的滿量程斜坡的旋轉波形。假設斜坡有固定的坡度;我們知道理想 ADC 的傳遞函數具有統一的步長。
例如,考慮對應于代碼 011 和 100 的步驟。這兩個步驟具有相同的寬度,因此斜坡信號應在步驟的轉換點之間產生相同的電壓變化(ΔV1 = ΔV2?2)。自從ΔV1V1= ΔV2,并且斜坡的斜率是恒定的,因此Δt1 = Δ?2t2這意味著斜坡輸入在相同的時間內落入不同代碼的輸入范圍內。換句話說,ADC 在每個輸出代碼上花費相同的時間。
基于此觀察,我們可以收集大量輸出樣本并創建代碼出現次數的直方圖。直方圖中的每個“bin”代表一個輸出代碼,每個bin的計數給出了該代碼出現的次數。該計數與 ADC 傳輸函數中相應步長的寬度成正比。
圖 3(c) 顯示了此示例的旋轉直方圖 - 請注意,與代碼 001 到 110 對應的 bin 都具有相同的計數(在本示例中為 8)。由于理想 ADC 中的第一步和最后一步通常定義為具有 0.5 LSB 和 1.5 LSB 的寬度,因此與代碼 000 和 111 對應的 bin 的計數分別為 4 和 12。
有人可能會說第一個和最后一個代碼實際上沒有定義的寬度,因為第一個代碼沒有下限,而代碼 111 沒有上限。如果輸入使 ADC 過載,這兩個代碼的出現頻率可能會比預期更高。事實上,在實際直方圖測試中,斜坡輸入的幅度被選擇為稍微超過 ADC 輸入范圍的兩端。這樣做是為了確保輸入信號執行 ADC 的所有代碼。因此,直方圖方法中通常會忽略第一個和最后一個 bin。
直方圖測試中常用的輸入信號
圖 3 所示的測試稱為線性斜坡直方圖測試。顧名思義,它使用斜坡輸入。但是,直方圖測試的輸入不一定是斜坡 - 正弦輸入是常見選擇,并且可以使用具有已知概率分布函數 (PDF) 的任何輸入。我們只需要計算理想 ADC 針對測試中使用的輸入信號類型產生的輸出 PDF。接下來,將測量的輸出直方圖與理論輸出直方圖進行比較,我們可以確定 ADC 的實際轉變點。
使用線性斜坡直方圖測試查找 DNL 誤差
現在我們已經討論了直方圖測試背后的理論,接下來讓我們使用直方圖方法來查找示例 ADC 的微分非線性 (DNL) 誤差。
首先,考慮圖 4(紅色曲線)中所示的非理想 3 位 ADC。
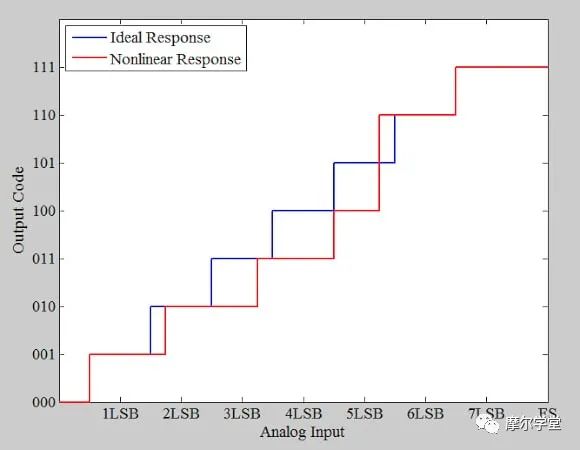
*圖 4.*理想(藍色)和非理想/非線性(紅色)示例 ADC 響應。圖片由 Steve Arar 提供
下面的圖 5 中提供了該示例 ADC 的 DNL 圖。請注意,缺少代碼 5 (101) 。
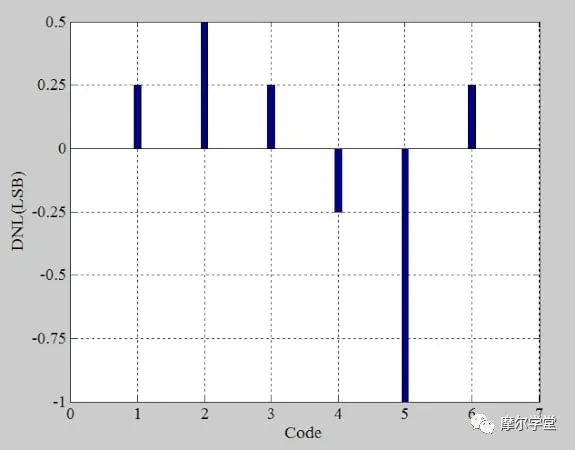
*圖 5.*示例 ADC 的微分非線性。圖片由 Steve Arar 提供
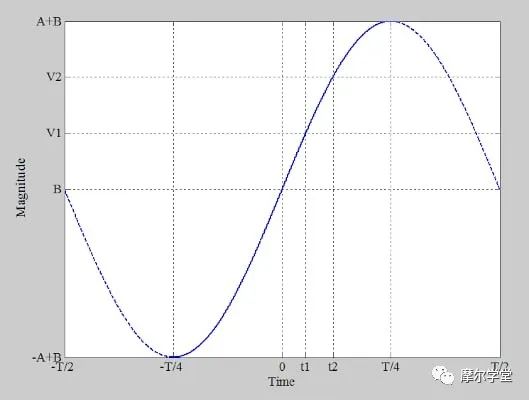
現在,使用上述滿量程范圍為 1 V 的傳遞函數,我們將以 40 kHz 的采樣率對周期性斜坡進行數字化。圖 6 顯示了結果。
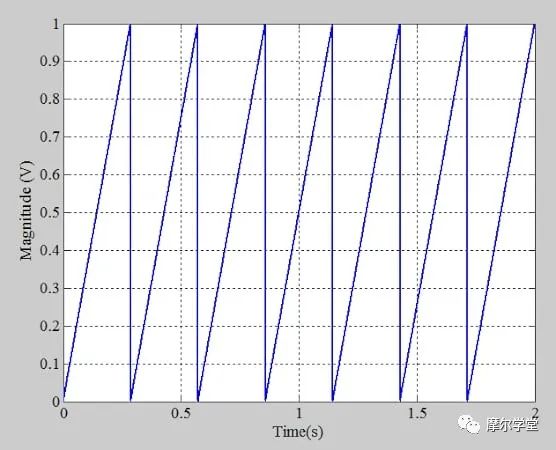
圖 6.重復周期性線性斜坡輸入,例如 ADC 直方圖測試。圖片由 Steve Arar 提供
斜坡周期(0.29 秒)遠大于樣本之間的時間,可以使用以下等式進行描述:
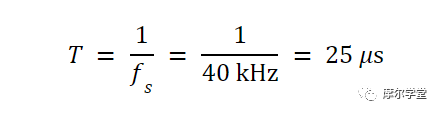
在哪里:
T是樣本之間的時間(以秒為單位)
f s是采樣頻率(以 Hz 為單位)。
換句話說,斜坡輸入相對于 ADC 采樣率緩慢變化。這允許每個 ADC 代碼被“命中”多次。
如果我們收集 80,000 個樣本,我們會得到如圖 7 所示的直方圖。
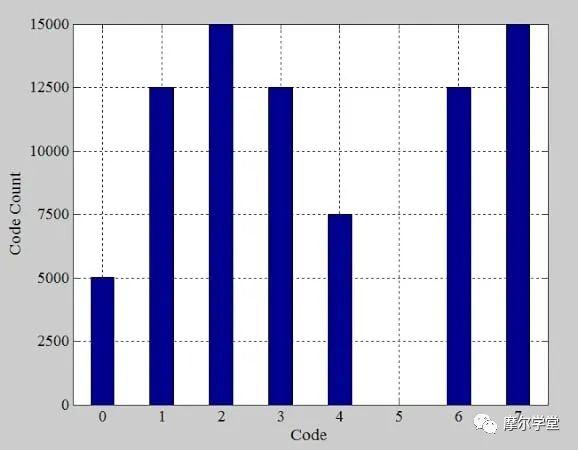
圖 7.示例 ADC 的數字代碼出現次數的直方圖。圖片由 Steve Arar 提供
Bin 5 的計數為零,表明代碼 5 (101) 丟失。檢查理想的 ADC 響應(圖 4 中的紅色曲線)表明,理想階躍的寬度等于第一個和最后一個轉換點之間的電壓間隔除以之間的階躍數:
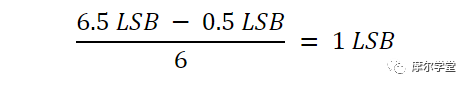
換句話說,理想臺階的寬度等于平均寬度。因此,具有理想寬度 (DNL = 0) 的代碼出現的次數等于每個 bin 的平均代碼計數。排除第一個和最后一個 bin,我們可以計算每個 bin 的平均命中數:
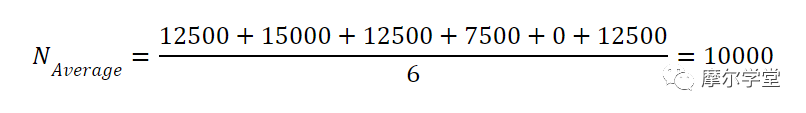
將 bin 高度除以平均代碼計數即可得到圖 8 中的歸一化直方圖。
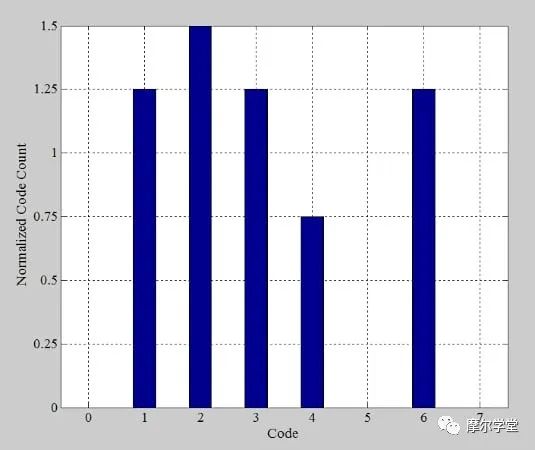
圖 8. ADC 測試示例的正態直方圖分布。圖片由 Steve Arar 提供
歸一化直方圖以最低有效位指定代碼寬度,我們之前確定理想步長的高度為 1 LSB。了解這一點后,我們可以通過從圖 8 的歸一化 bin 計數中減去 1 LSB 來生成 DNL 信息(圖 9)。我們的結果與圖 5 中的 DNL 圖一致。
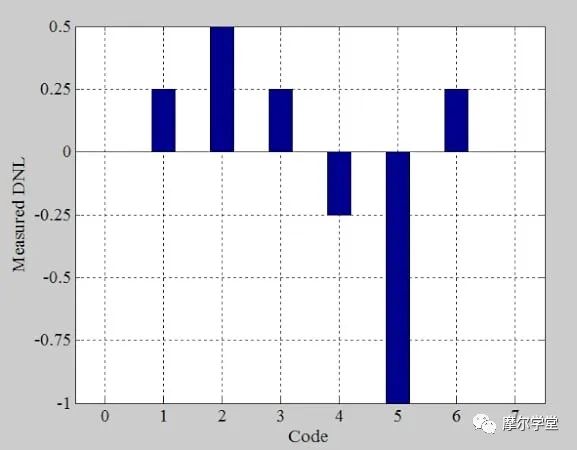
*圖 9.*示例 ADC 的 DNL。圖片由 Steve Arar 提供
如果采取適當的預防措施,線性斜坡直方圖方法可用于測量 16 位或更高分辨率的 ADC 的微分非線性。準確測量積分非線性 (INL) 更具挑戰性。
使用線性斜坡直方圖測試來測量 INL
INL規范描述了實際傳遞函數的轉變點與理想值的偏差。INL是DNL誤差的累積效應,因此第m個代碼的INL可以通過應用以下等式找到:
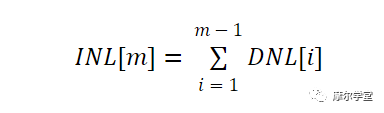
原則上,可以將DNL信息代入上述方程來確定INL誤差。然而,在實踐中,有幾個誤差源妨礙我們準確測量 INL。
測試電路參數和 ADC 特性的變化會導致 INL 測量誤差。測試電路的變化可能來自電源、參考電壓或輸入信號發生器;可變的 ADC 特性包括偏移和增益。
上式中的求和本質上是在測量時間內累積所有這些誤差,可能會導致10 位以上線性度的錯誤結果。
緩慢的測量系統會加劇漂移問題——如果它無法跟上 ADC 的高采樣率,則收集所需數量的樣本將需要更長的測量時間。如果漂移誤差是限制因素,我們可以使用快速傅立葉變換 ( FFT ) 測試來測量 ADC 諧波失真,這是 INL 的主要影響。FFT 測試需要的樣本數量要少得多,因此對漂移不太敏感。
此外,線性斜坡直方圖測試假設輸入斜坡是完全線性的。輸入中的任何非線性都會直接轉化為我們的 INL 測量中的誤差。這限制了基于斜坡直方圖的INL 測量對 12 位左右的 ADC的使用。為了解決這個問題,我們可以使用正弦輸入進行直方圖測試,因為可以輕松生成低噪聲、純正弦輸入。
審核編輯:劉清
-
轉換器
+關注
關注
27文章
8721瀏覽量
147405 -
adc
+關注
關注
98文章
6510瀏覽量
544987 -
FFT
+關注
關注
15文章
436瀏覽量
59411 -
模數轉換器
+關注
關注
26文章
3208瀏覽量
126876
原文標題:直方圖測試模數轉換器(ADC)
文章出處:【微信號:moorexuetang,微信公眾號:摩爾學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
ADC模數轉換器介紹




 直方圖測試模數轉換器(ADC)介紹
直方圖測試模數轉換器(ADC)介紹










評論