使用(s域)傳遞函數(shù)分析串聯(lián)RLC電路系統(tǒng)。
線性非時變系統(tǒng)定義給我們帶來了許多數(shù)學(xué)工具,也包含卷積積分,傅里葉變換和拉普拉斯變換。這些工具曾經(jīng)是我學(xué)生時代的夢魘,以至于它們對我來說不是物理電路,也不是系統(tǒng),更不是數(shù)學(xué)。現(xiàn)在鼓起勇氣,再次入夢。
注,如無特殊聲明,本文中提到系統(tǒng)均為線性非時變系統(tǒng)。
分析下圖RLC電路。
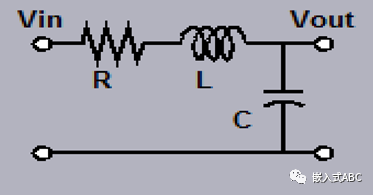
引入(運算)阻抗得到電路傳遞函數(shù)如下,這是一個二階系統(tǒng)。
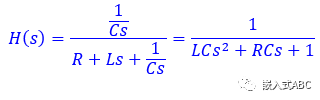
以后我們也會討論到,即使不執(zhí)行拉普拉斯反變換,不需要求得最后的時域解也能夠分析RLC電路系統(tǒng)的某些特征。
傳遞函數(shù)
傳遞函數(shù)是一個數(shù)學(xué)模型,表示依照每個可能輸入值輸出的行為,即系統(tǒng)的傳輸增益。輸入值定義為激勵,在傳遞函數(shù)定義中激勵必須為獨立激勵,而非受控激勵。輸出值定義為響應(yīng)。
s域(復(fù)頻域)系統(tǒng)傳遞函數(shù)為
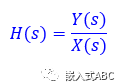
X(s)為激勵拉普拉斯轉(zhuǎn)換函數(shù),Y(s)為響應(yīng)拉普拉斯轉(zhuǎn)換函數(shù)。
這里還有一個關(guān)鍵假設(shè),即系統(tǒng)的所有初始條件均為零。或者按照電路課本中說法為零狀態(tài)響應(yīng)。當然若初始條件不為零時,拉普拉斯變換也會將初始條件適當?shù)剞D(zhuǎn)換為激勵函數(shù)以得到電路的全響應(yīng)(當然包含零輸入響應(yīng))。不過這些初始條件轉(zhuǎn)換的激勵對應(yīng)響應(yīng)的傳輸增益(或者說傳遞函數(shù)),不同于前面定義的傳遞函數(shù)。
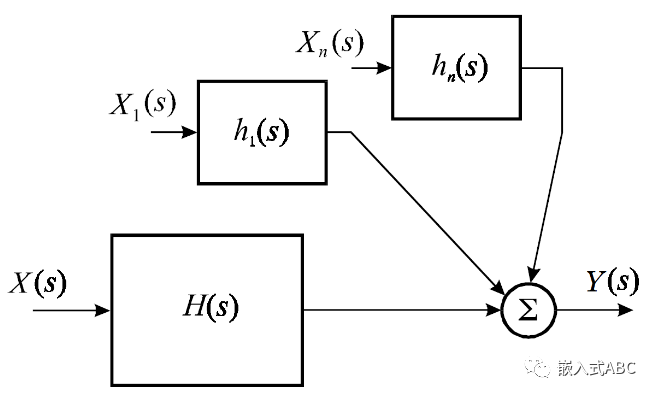
定義初始條件拉普拉斯轉(zhuǎn)換函數(shù)為X i (s),相應(yīng)傳遞函數(shù)為H i (s)。當然也可以推廣到為多輸入系統(tǒng)。由疊加定理可得
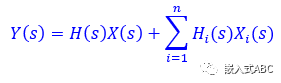
域
域是分析信號與系統(tǒng)的不同視角。簡單說基于自變量t或函數(shù)f(t)的分析視角為時域,基于自變量jω或函數(shù)F(jω)的分析視角為頻域,基于自變量s=σ+jω或函數(shù)F(s)的分析視角為復(fù)頻域。
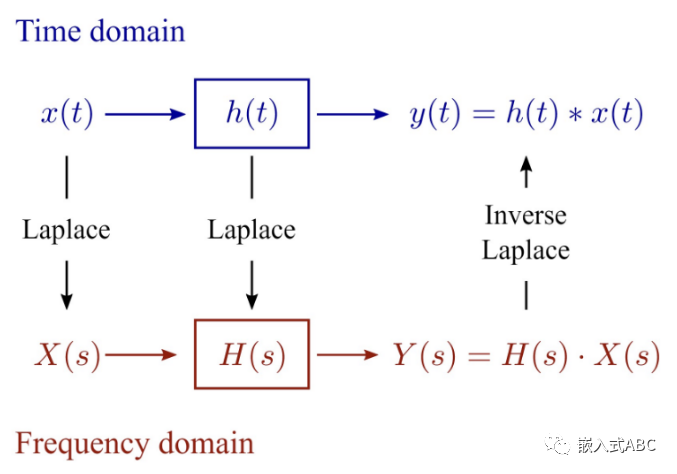
時域
時域?qū)?yīng)于真實世界。我們已經(jīng)習(xí)慣了時域,習(xí)慣了時間,時間并被定義為這個世界的一個維度。
麥克斯韋方程組也基于時域。于是(模擬)電路系統(tǒng)中,對于任意輸入信號,時域分析法提供了一種分析電路系統(tǒng)特性(輸入輸出之間特定關(guān)系)的方法。微分方程提供了研究這一問題的方法,它利用導(dǎo)數(shù)概念來求解函數(shù)在某一點附近的變化率。這是一個用于表示函數(shù)在輸入量變化了一定值時,輸出量變化率的數(shù)學(xué)工具。于是上述RLC串聯(lián)電路時域傳遞函數(shù)或響應(yīng)的求解就是二階齊次微分方程的求解。微分方程求解是另一個夢魘。
而且讓我不解的是為什么頻域或復(fù)頻域比我們已經(jīng)習(xí)慣了的時域在理解信號/電源完整性(阻抗概念)和電路系統(tǒng)穩(wěn)定性等問題中更加具有洞悉力。
頻域
傅里葉變換方程
接收某個時間函數(shù)并輸出頻率函數(shù),告訴我們信號中含有那些頻率或正弦曲線。
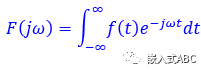
歐拉等式方程
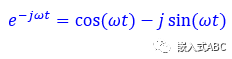
代入傅里葉變換方程得到
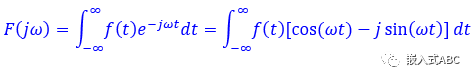
正弦波是頻域中唯一存在的波形,正弦波是頻域的語言。時域中任何波形都可由正弦波的組合完全且唯一地描述。
電路系統(tǒng)中傅里葉變換提供了非正弦周期電流電路的一種新的分析方法-諧波分析法,它是正弦電流電路分析方法(適用于正弦穩(wěn)態(tài)分析的相量法)的推廣。或者說它比正弦電流電路分析方法多了一個維度,在頻譜概念中將會體會到這一點。傅里葉變換同樣適用于非周期性電流電路(如瞬態(tài)響應(yīng)中脈沖信號/沖擊響應(yīng))的分析,只不過其頻譜將由離散頻譜變?yōu)檫B續(xù)頻譜。
s****域(復(fù)頻域)
拉普拉斯變換方程
拉普拉斯變換告訴我們函數(shù)中存在那些正弦曲線和指數(shù)曲線。
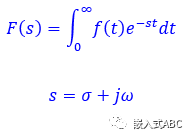
代入拉普拉斯變換方程得到
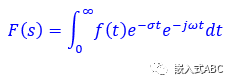
傅里葉變換是拉普拉斯變換的一種特例。一個函數(shù)的拉普拉斯變換就是該函數(shù)乘于一個指數(shù)項的傅里葉變換,對σ在實數(shù)域上的所有值,執(zhí)行此操作,即可獲得整個拉普拉斯變換。拉普拉斯變換比傅里葉變換又多了一個維度。
拉普拉斯變換常用于研究反饋系統(tǒng)的全響應(yīng),包括瞬態(tài)響應(yīng),如脈沖沖擊或階躍輸入產(chǎn)生的響應(yīng)。即系統(tǒng)對初始條件或突然施加信號的時間響應(yīng),而傅里葉變換主要關(guān)注系統(tǒng)的穩(wěn)態(tài)響應(yīng)。
拉普拉斯變換的性質(zhì)
(時域)導(dǎo)數(shù)性質(zhì)
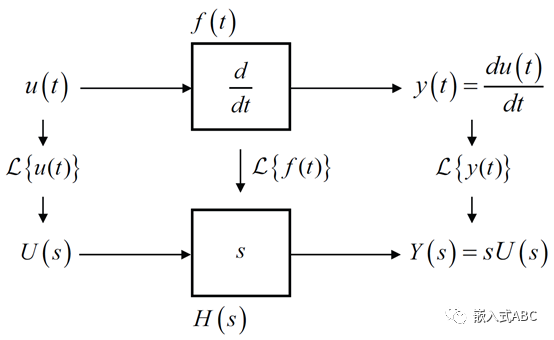
(時域)積分性質(zhì)
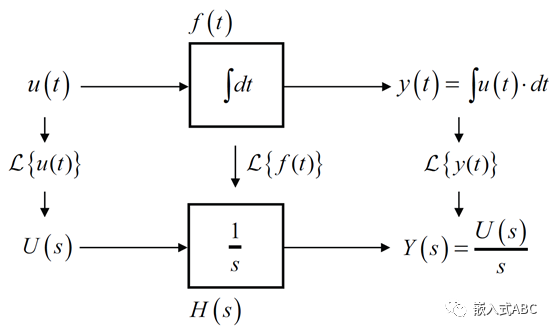
拉普拉斯變換的另一重要特點,即拉普拉斯變換的性質(zhì)可以讓我們把微積分運算轉(zhuǎn)化為代數(shù)運算。
總結(jié)
許多情況下傅里葉變換和拉普拉斯變換或者頻域和復(fù)頻域比時域更具有洞悉力,能更快的找到解決方法。
而且讓我不解的是為什么頻域或復(fù)頻域比我們已經(jīng)習(xí)慣了的時域在理解信號/電源完整性(阻抗概念)和電路系統(tǒng)穩(wěn)定性等問題中更加具有洞悉力。
也許這來自于(正弦與指數(shù)等)幾何函數(shù)的理解與空間維度的增加或降低,給我們帶來直觀的理解。
-
串聯(lián)電路
+關(guān)注
關(guān)注
6文章
160瀏覽量
25971 -
傅里葉變換
+關(guān)注
關(guān)注
6文章
442瀏覽量
42882 -
拉普拉斯變換
+關(guān)注
關(guān)注
1文章
32瀏覽量
10247 -
RLC電路
+關(guān)注
關(guān)注
2文章
26瀏覽量
7261
發(fā)布評論請先 登錄
相關(guān)推薦
放大器的傳遞函數(shù)-誤差放大器、電壓放大器、電流放大器的傳遞函數(shù)導(dǎo)出
開環(huán)傳遞函數(shù)是怎樣影響系統(tǒng)的?
傳遞函數(shù)和控制Block(上)
線性電路傳遞函數(shù)的快速分析技術(shù)
基于Butterworth標準傳遞函數(shù)設(shè)計
傳遞函數(shù)極點和零點的影響是什么
傳遞函數(shù)是怎么定義的以及如何寫出傳遞函數(shù)?
傳遞函數(shù)的頻率特性
各轉(zhuǎn)換器的傳遞函數(shù)-開關(guān)的導(dǎo)通電阻對傳遞函數(shù)的影響
傳遞函數(shù)中的極點和零點有何影響?
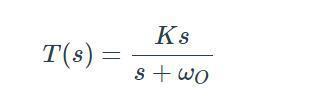
如何建立傳遞函數(shù)?


















評論