s域
濾波器的響應可以用s域傳遞函數(shù)表示;變量s來自拉普拉斯變換,代表復雜的頻率。例如:
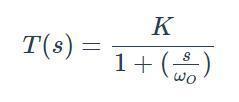
該傳遞函數(shù)是一階低通濾波器頻域特性的數(shù)學描述。s域表達式有效地傳達了一般特征,如果我們想要計算特定的振幅和相位信息,我們所要做的就是用jω代替s,然后在給定的角頻率下評估表達式。因為從未見過具有以K和ωO表示的元件值的電路圖,所以你可能想知道其中K和ωO來自哪里。這里的想法是K和ωO就像一個模板的部分,并在接下來的部分,我們將看看模板和電路圖之間的關系。
s域電路分析
RC低通濾波器是與頻率相關的分壓器。 在s域分析中,電阻器的阻抗為R,電容器的阻抗為 1/sC。
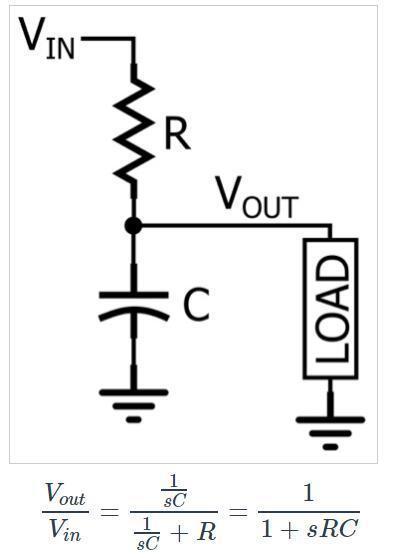
如果比較這個表達式與標準化傳遞函數(shù),可以看出K = 1且ωO= 1/RC。 一旦你知道K和ωO代表什么,使用標準化形式的便利就變得清晰了:K是電路在DC上的增益,ωO是截止頻率。 因此,通過比較電路的傳遞函數(shù)與標準化傳遞函數(shù),可以立即為一階低通濾波器的兩個定義特征表達式,即DC增益和截止頻率。另一種標準形式的一階低通傳遞函數(shù)如下:
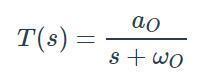
如果我們將分子和分母除以RC,我們可以將電路的傳遞函數(shù)擬合到這個模板中:
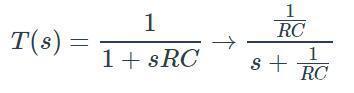
因此,aO = 1/RC和ωO= 1/RC。這種形式并沒有直接給DC增益,但如果我們評估s = 0的標準化表達式,我們就有了:
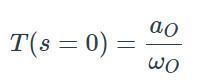
這意味著我們的RC濾波器的DC增益為(1/RC)/(1/RC)= 1,DC的單位增益正是我們對無源低通濾波器的期望。
理解截止頻率
我們已經(jīng)看到ωO在標準傳遞函數(shù)表示截止頻率,但這一事實的數(shù)學基礎是什么?首先,讓我們將標準的s域傳遞函數(shù)轉(zhuǎn)換為等效的jω傳遞函數(shù)。
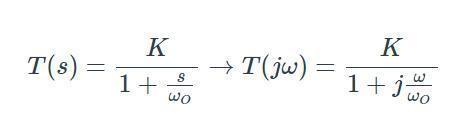
現(xiàn)在讓我們以截止頻率評估表達式。
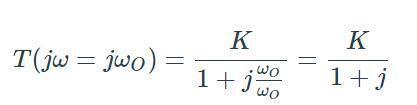
分母是一個復數(shù),因此振幅很大。
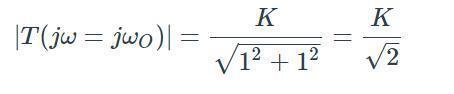
由于K是DC增益,幅度為1V的極低頻輸入信號將導致幅度為KV的輸出信號。 如果輸入頻率增加到每秒ωO弧度,輸出幅度將為K/√2。 K/√2對應于-3 dB,你可能知道,截止頻率的另一個名稱是-3 dB頻率。
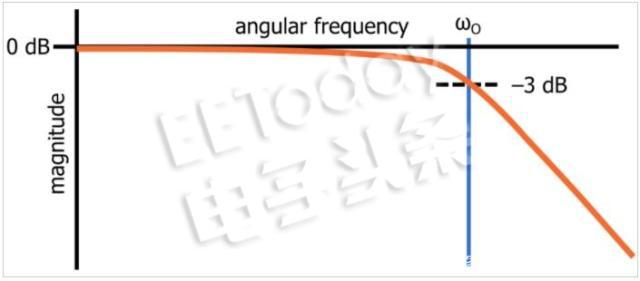
一階無源低通濾波器的振幅響應圖,當它被繪制為以dB為單位的振幅與對數(shù)頻率的關系。
這種直接的傳遞函數(shù)分析清楚地證明了截止頻率只是濾波器振幅響應相對于極低頻振幅響應降低3dB的頻率。
截止頻率和相移
低通濾波器的截止頻率對于電路的相位響應也具有特殊意義。如果我們以x + jy的形式寫出一個復數(shù),我們按如下方式計算相位:
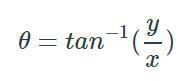
因此,我們的RC低通濾波器的整體相位響應是
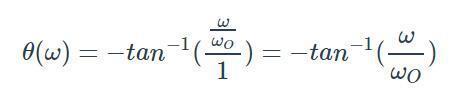
如果我們在ω = ωO處評估這個表達式,相移是
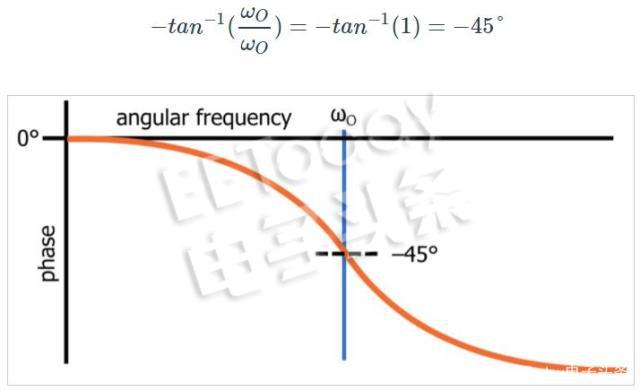
當相移相對于對數(shù)頻率時一階無源低通濾波器的相位響應圖。
由一階低通濾波器產(chǎn)生的最大相移為90°,因此該分析告訴我們截止頻率是電路相位響應的“中心”,換句話說,它是濾波器的頻率產(chǎn)生一半的最大相移。
-
電容器
+關注
關注
64文章
6308瀏覽量
100620 -
濾波器
+關注
關注
161文章
7919瀏覽量
179506 -
電阻器
+關注
關注
21文章
3827瀏覽量
62564 -
低通濾波器
+關注
關注
14文章
485瀏覽量
47636 -
拉普拉斯變換
+關注
關注
1文章
32瀏覽量
10212
發(fā)布評論請先 登錄
相關推薦
無源低通濾波器電路,有源低通濾波器原理圖
請問模擬濾波器 傳遞函數(shù)有什么特點?
我想自己設計濾波器的傳遞函數(shù),怎么在Labview中實現(xiàn)?
ua741構(gòu)成的低通濾波器其傳遞函數(shù)和截止頻率怎么計算?
低通濾波器傳遞函數(shù)
低通濾波器的傳遞函數(shù)簡介
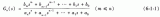
基于使用雙極點RC低通濾波器推導代數(shù)傳遞函數(shù)
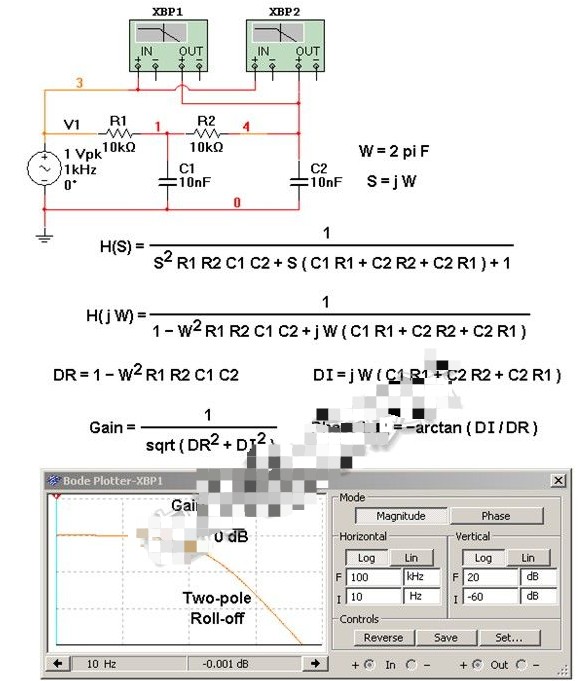
傳遞函數(shù)極點和零點的影響是什么
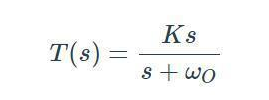
一階高通濾波器傳遞函數(shù)如何導致高通量和相位響應呢?
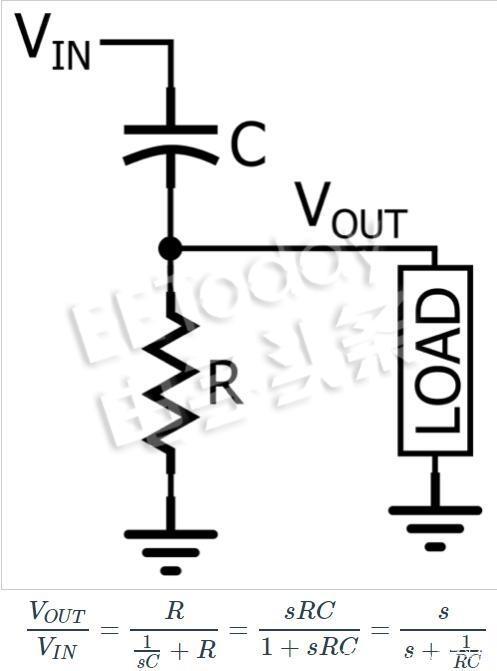
傳遞函數(shù)中的極點和零點有何影響?
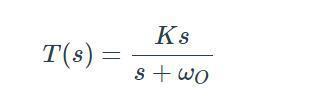




 低通濾波器的傳遞函數(shù)簡析
低通濾波器的傳遞函數(shù)簡析










評論