3.1
帶寬的定義
帶寬用于表示頻譜中最高的有效正弦波頻率分量值。為了充分近似刻畫時域波形的特征, 這是需要包含的最高正弦波頻率。所有高于帶寬的頻率分量都可忽略不計。
帶寬這一術語最初在射頻領域中用于表示信號的頻率范圍。在射頻應用中,以幅度和相位的形式來調制載波頻率,是一種典型的方式。信號中的各頻譜分量組成了一個頻帶。這種射頻信號的頻率范圍就稱為帶寬。一個射頻信號的帶寬定義了不同的通道所能傳輸信號的密集程度。
對于數字信號,帶寬同樣指的是信號頻譜中的頻率范圍。只不過對于數字信號而言,低頻范圍起始于直流分量并延伸到最高頻率分量。在數字信號領域里,因為最低頻率是直流,所以帶寬總是對應于最高的有效正弦波頻率分量值。
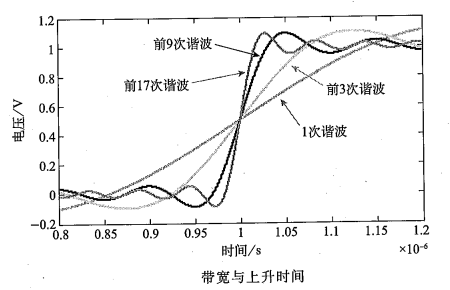
如上圖所示,如果只用0次、1次和3次諧波合成時域波形,那么所得波形的帶寬只達到3次諧波的值,即3GHz。設計時,這個波形的最高正弦波頻率分量是3GHz,其他正弦波頻率分量的幅度為零。
如果增加更高次諧波用于生成波形,那么設計的帶寬9GHz,17GHz。如果取出圖中上升邊最短的波形,并把它變換到頻域中,則其頻譜中含有的諧波分量從0次諧波一直到17次諧波,超過17次諧波的所有分量都為零。這個波形中的最高有效正弦波頻率分量就是17次諧波,即此波形的帶寬為17GHz。
3.2
帶寬對上升邊的影響
第二章已經說明了由信號的頻譜可以得到時域波形,實質上是傅里葉逆變換過程,只不過對于周期信號來說,這一傅里葉逆變換過程更明顯地表現為一系列單頻信號的加權和的形式。
對于理想方波信號,上升時間為0,每一個頻率分量都是必需的,因此,理論上理想方波信號帶寬是無窮大的。盡管如此,無窮大的帶寬對實際工程應用沒有什么實際意義,信號頻譜中各個頻率分量的貢獻是不同的。
我們已經知道了頻率趨于無窮大時方波信號的頻譜幅度以一20 dB/十倍頻程的速度衰減,對于某個頻率分量,如果其頻譜幅度足夠小,以至于我們可以把它對波形的貢獻忽略掉,那么我們就可以不必考慮它的影響,這就是定義信號帶寬的根本原因。
使用有限帶寬的頻譜來代替無窮寬的頻譜,進而得到一個對原信號的可接受的近似,對工程應用更具有實際意義。
通過仿真實驗分析信號頻譜中各個頻率分量是如何影響信號時域波形的。
下圖是理想方波的級數展開式:

下圖分別是1f、3f、11f、39f 帶寬的波形圖


至此,我們得到結論:上升時間越小,信號帶寬越大,說明高頻成分對信號的貢獻越大。如果信號上升時間較長,使用相對較小的帶寬就可以合成信號波形,說明高頻成分的貢獻要小得多。反映在頻譜上,高頻成分的頻譜幅度相對較小,因此,上升時間越長,頻譜中高頻成分衰減越快。
帶寬和上升時間的關系:

3.3
時鐘頻率與帶寬
眾所周知,帶寬與信號的上升邊直接有關。我們并非總能知道信號的上升邊,但是卻需要知道它的帶寬。若給定一個簡單的假設,就可以從信號的時鐘頻率估算出它的帶寬。需要注意的是,不是時鐘頻率而是上升邊決定帶寬。
為了通過信號的時鐘頻率估計它的帶寬,必須做一個非常重要的假設,即首先估計出時鐘波形典型的上升邊。如果不知道上升邊與周期的比值,則一個合理的概括是:上升邊是時鐘周期的7%。
這與許多微處理器板和ASIC驅動板級總線的情況接近。因此,可以據此估算時鐘波形的帶寬。即帶寬是時鐘頻率的5倍:BW_clock= 5 x F_clock。或者說,時鐘波形中典型的最高正弦波頻率分量就是5次諧波。
-
微處理器
+關注
關注
11文章
2273瀏覽量
82640 -
信號完整性
+關注
關注
68文章
1416瀏覽量
95571 -
ASIC芯片
+關注
關注
2文章
92瀏覽量
23824 -
頻譜儀
+關注
關注
7文章
342瀏覽量
36151 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42665
發布評論請先 登錄
相關推薦
2011信號及電源完整性分析與設計
信號完整性分析
基于PCB信號完整性的反射設計
聽懂什么是信號完整性





 信號完整性的信號帶寬對上升邊的影響
信號完整性的信號帶寬對上升邊的影響













評論