本文是西安交通大學&蘇黎世聯邦理工學院的趙子祥博士在ICCV2023上關于多模態圖像融合的最新工作，題目為：DDFM: Denoising Diffusion Model for Multi-Modality Image Fusion。本文首次在多模態圖像融合領域采用了擴散模型，很精彩的一篇工作，就是數學推導難住了我這個工科生。本文提出的模型DDFM的完整流程是通過圖1的c來實現，而具體到每一步從fT到fT?1的過程是通過圖3的流程實現，也就是本文的核心之一：傳統vanilla DDPM模型中有ft→f~0|t→ft?1的過程，而本文會在f~0|t到ft?1之間通過EM算法增加一個中間量f^0|t來解決最大化似然問題（即解決下文中公式13），整個過程變為ft→f~0|t→f^0|t→ft?1。而這個過程是為了解決本文另一個核心，即條件生成問題。具體則是將圖像融合損失函數優化問題轉化為最大似然問題。綜上所述，可以這樣理解本文DDFM的融合思想：首先通過自然圖像預訓練的DDPM模型進行無條件生成，得到初步結果（目的使融合結果符合自然圖像的生成先驗）。隨后對初步生成結果進行條件生成（似然修正）。通過將融合問題轉化為一個含隱變量的極大似然估計問題（公式8轉換為公式13），再通過EM算法來解決該極大似然估計問題，完成條件生成。以上兩步，構成ft→ft?1的單次迭代，而最終經過T次迭代后，得到融合圖像f0。

本文：https://https://arxiv.org/abs/2303.06840
代碼：https://github.com/Zhaozixiang1228/MMIF-DDFM

文章題目與作者信息：

DDFM: Denoising Diffusion Model for Multi-Modality Image Fusion

在CVer微信公眾號后臺回復：DDFM，可以下載本論文pdf、代碼

下面是正文部分。

多模態圖像融合目的在于組合不同模態下的圖像并保留互補信息，為了避免GAN模型諸如訓練不穩定和缺少解釋性這類問題，同時利用好強大的生成先驗，本文提出了基于去噪擴散概率模型 Denoising diffusion probabilistic model (DDPM) 的融合算法。融合任務會在DDPM采樣框架下設計為條件生成問題，并被分成無條件生成子問題和最大似然子問題。其中最大似然子問題通過具有隱變量的分層貝葉斯方式建模，并使用期望最大化算法進行推理。通過將推理解決方法整合進擴散采樣迭代中，本文方法可以生成高質量的融合圖像，使其具備自然的圖像生成先驗和來自源圖像的跨模態信息。需要注意的是本文方法需要無條件預訓練生成模型，不過不需要fine-tune。實驗表明本文在紅外-可見光融合以及醫學影像融合中效果很好。

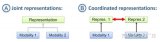
紅外-可見光融合IVF就是要避免融合圖像對可見光的光照敏感，避免對紅外的噪聲和低分辨率敏感。基于GAN的融合方法如下圖a，會有一個生成器得到融合圖像，然后判別器來決定融合圖像和哪個模態的源圖像更接近。基于GAN的方法容易出現訓練不穩定的問題，同時有缺少解釋性等問題。另外由于基于GAN的方法是一個黑箱，很難理解GAN的內在機制和行為，讓可控的融合變得困難。

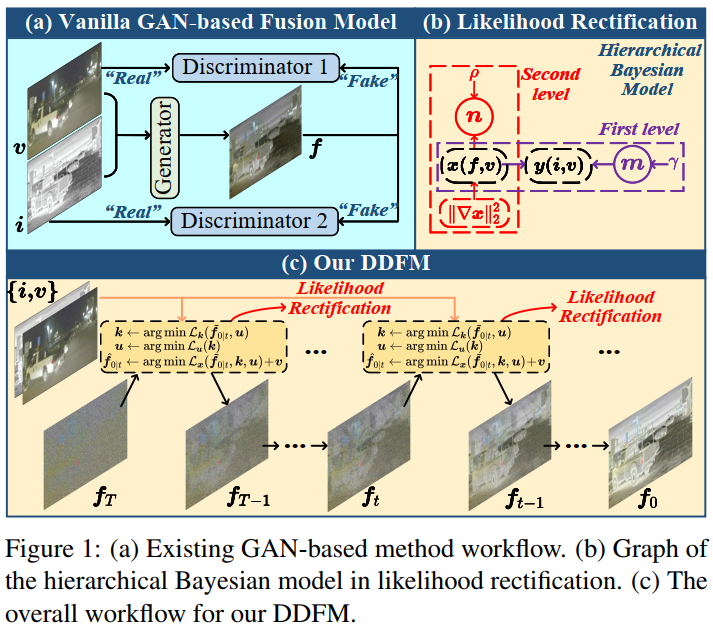
近來去噪擴散概率模型 Denoising diffusion probabilistic model (DDPM)在圖像生成中獲得很多進步，通過對一張noise-corrupted圖像恢復為干凈圖像的擴散過程進行建模， 可以生成質量很好的圖像。基于Langevin擴散過程的DDPM利用一系列逆擴散步驟來生成效果很好的合成圖像。對比GAN的方法，DDPM不需要判別器，因此緩解了基于GAN方法諸如訓練不穩定和模式崩潰等問題。另外，由于這類方法是基于擴散過程的，所以基于DDPM的生成過程具有可解釋性，可以更好地理解圖像生成過程。

因此本文提出了 Denoising Diffusion image Fusion Model (DDFM)，其結構如上圖的c，本文將條件生成任務設計為基于DDPM的后驗采樣模型，進一步可以被分為無條件生成擴散問題和最大似然估計問題，第一個問題可以滿足自然圖像先驗，第二個問題通過似然矯正來限制生成圖像和源圖像之間的相似性。和判別式方法相比，用DDPM對自然圖像先驗建模可以得到更好的細節生成，這點很難通過損失函數的設計來達到。作為生成模型，DDFM效果穩定，生成效果可控。綜合來說本文貢獻如下：1.引入基于DDPM的后驗采樣模型來進行多模態圖像法融合任務，包含無條件生成模塊和條件似然矯正模塊，采樣的圖像只通過一個預訓練的DDPM完成，不需要fine-tune；2.似然矯正中，由于顯式獲得似然不可行，因此將優化損失表示為包含隱變量的概率推理問題，可以通過 EM 算法來解決，然后這個方法整合進DDPM回路中完成條件圖像生成；3.實驗表明本文方法在IVF和醫學影像融合中都可以獲得很好的結果。

Score-based擴散模型：首先看score SDE 方程。擴散模型目標是通過反轉一個預定義的前向過程來生成樣本，這個前向過程就是將干凈的樣本x0通過多個加噪過程，逐步轉換成接近高斯信號的樣本xT，其過程可以用隨機微分方程表示，如下式。

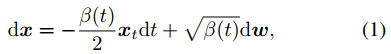
其中dw是標準Wiener過程，β(t)是有利于variance-preserving SDE 的預定義噪聲表。

該前向過程可以被反轉并保持SDE的形式，如下式。

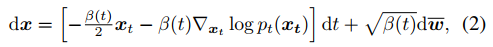
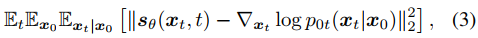
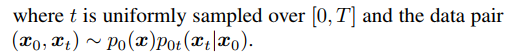
下來是使用擴散模型采樣。無條件擴散生成過程從一個隨機噪聲向量xT開始，根據式2的離散化形式進行更新。也可以將DDIM的方式理解采樣過程，即score函數可以被看做一個去噪器，在迭代t中，從狀態xt預測去噪結果x~0|t，如下式。

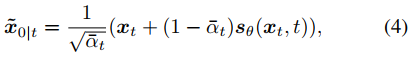
這樣x~0|t就可以表示給定xt時，x0的估計。

具體更新的方式如下。

使用上面的方式，直到x0被生成。

本文基于DDPM和以往方法的對比：傳統基于優化的方法主要是收到人工設計損失函數的限制，這可能會讓這類方法在數據分布發生改變時融合效果不佳。雖然整合自然圖像先驗可以提供額外的知識，但是只用損失函數來建模是遠遠不足的。和GAN方法相比，本文的擴散模型方法可以避免不穩定的訓練和模式坍塌，通過每次迭代過程中對源圖像生成過程的矯正和基于似然的優化就可以得到穩定的訓練和可控融合了。

模型結構

通過擴散后驗采樣來融合圖像：使用i、v、f分別表示紅外、可見光、融合圖像，其中融合圖像與可見光圖像均為RGB彩圖。期望f的后驗分布可以通過i和v建模，這樣f就可以通過后驗分布中采樣得到了。受到式2的啟發，擴散過程的逆SDE可以用下式表示。

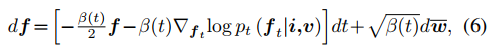
score函數可以通過下式計算。

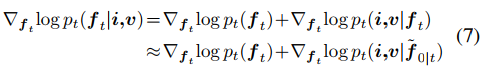
其中f~0|t是給定ft后，從無條件DDPM中對f0的估計。上式來源于貝葉斯理論，其近似方程可以看原文引用的文獻。上式中的第一項表示無條件擴散采樣的score函數，可以通過預先訓練的 DDPM 輕松推到出來。下一節將解釋第二項的獲得方式。

圖像融合的似然矯正：傳統圖像退化反轉問題，如下式。

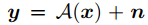
x是groundtruth，y是測量方法，A是已知的，可以顯式地獲得其后驗分布，然后在圖像融合問題中，想要在給定ft或者f~0|t情況下，獲得i和v的后驗分布是不可能的。為了解決這個問題，首先需要建立優化函數和概率模型的似然之間的關系。下面使用 f 來表示f~0|t。

圖像融合通常使用的損失函數如下式。

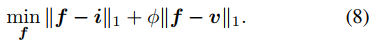
使用x=f-v和y=i-v來替換變量，可以得到下式。

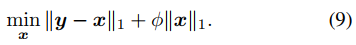
由于y已知，而x未知，那么上式中的第一項就對應于下式k恒為1的回歸模型。

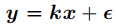
而根據正則項和噪聲先驗分布之間的關系，?必須是拉普拉斯噪聲，x則是服從拉普拉斯分布。那么根據貝葉斯準則，有下式。

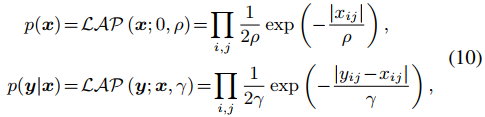
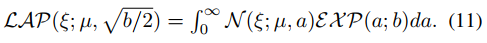
因此式10中的p(x)和p(y|x)可以被寫為下面的分層貝葉斯框架。

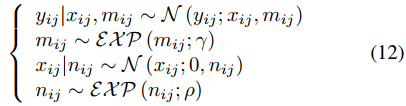
其中i和j分別表示圖像的高和寬。通過上式，就可以將式9中的優化問題轉換為一個最大似然推理問題。

另外，全變分懲罰項也可以加到融合圖像f中，以更好地從可見光圖像v中保留紋理信息，其形式如下，先對x求梯度后再計算L2范數。

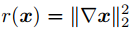
最終，概率推理問題的對數似然函數用下式表示。

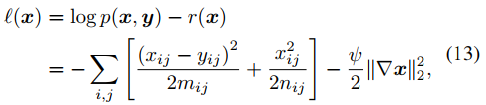
這個分層貝葉斯模型的概率圖即為圖1的b形式。

這里將式8的優化問題轉換為了式13最大似然問題的概率模型。另外和傳統方法中人工調整參數懲罰項參數?不同，本文方法可以通過推理隱變量，自適應地更新參數?，讓模型可以更好地擬合不同數據分布。

下面是通過EM算法推理似然模型。為了解決式13的最大對數似然問題，也就是可以被看做包含隱變量的優化問題，本文使用Expectation Maximization, EM算法來獲得x。EM步驟如下。

在E步驟中，由下面的命題2來計算隱變量條件期望的計算結果，并得到Q方程的推導。

命題2：隱變量1/m和1/n的條件期望計算如下式，證明過程可以看原文。

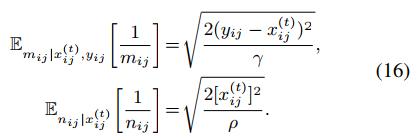
然后，可以通過貝葉斯理論得到m的后驗概率，如下。

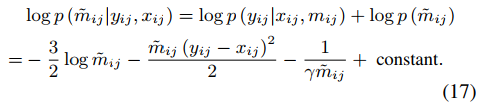
同時m的后驗概率可以通過下式計算。

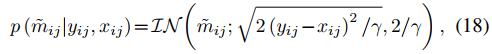
其中IN是逆高斯分布。

對于n也可以用式17相同的方式計算，如下式。

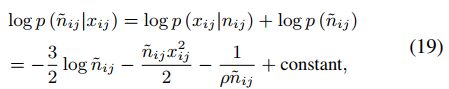
那么n也可以轉換為使用逆高斯分布計算的方式，如下式。

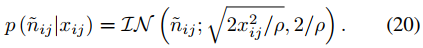
最終，1/m和1/n的條件期望就是式18和20中逆高斯分布的平均參數。

那么Q方程就可以通過下式推到得到。

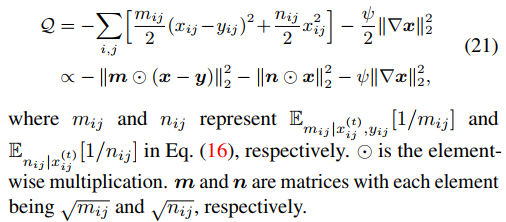
M步驟中，需要最小化關于 x 的負 Q 函數，用half-quadratic splitting算法來處理該問題，如下式。

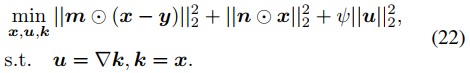
可以進一步轉化為如下無約束優化問題。

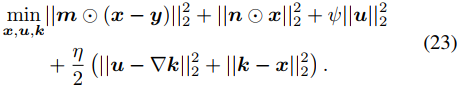
式中的未知變量k、u、 x 可以通過坐標下降方式迭代求解。

k的更新是反卷積過程，如下式。

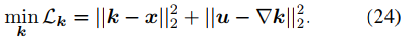
可以采用快速傅里葉變換及其逆變換算子來得到，如下式。

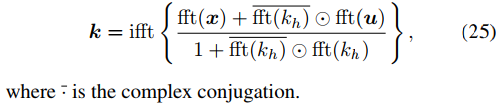
u的更新是L2范數懲罰回歸問題，如下式。

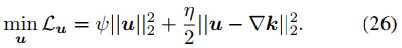
其計算方式如下。

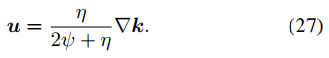
x的更新是最小二乘問題，如下式。

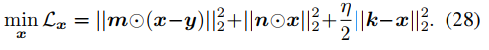
其計算方式如下。

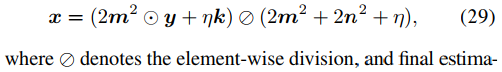
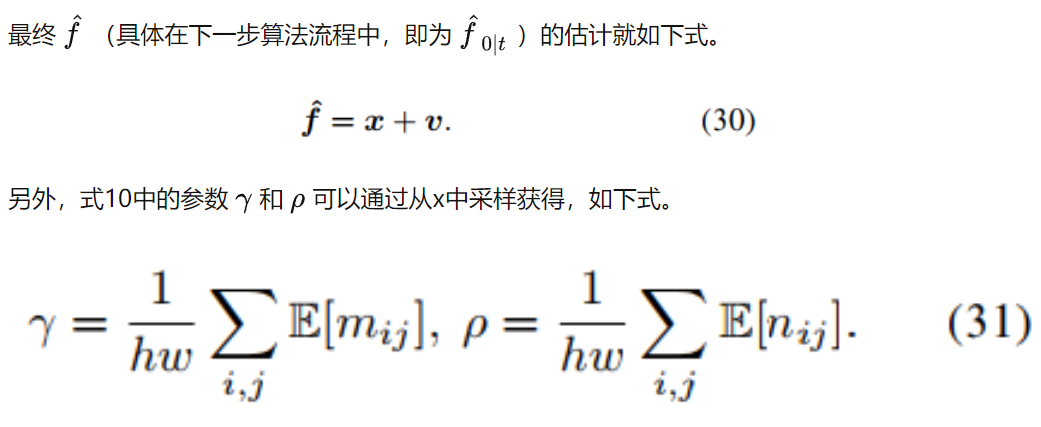
DDFM：前面部分描述是從已有損失函數中獲得分層貝葉斯模型，通過EM算法來進行推理。下面講述本文DDFM將推理方法和擴散采樣整合到同一個框架內，根據輸入v和i獲得融合圖像f，算法流程如下。

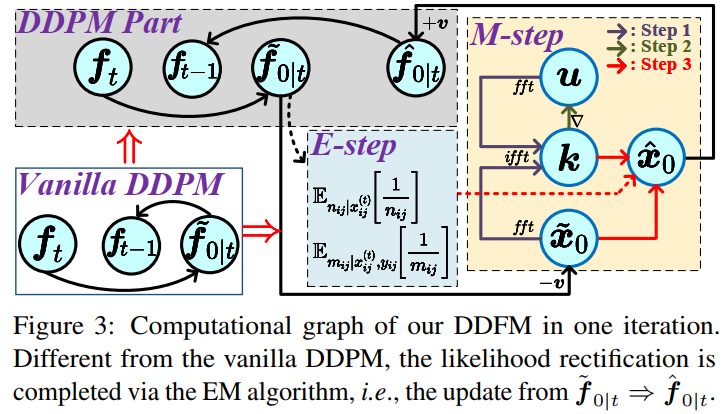
DDFM中包含兩個模塊，一個是無條件擴散采樣模塊unconditional diffusion sampling (UDS) ，一個是似然矯正，也就是EM模塊。UDS模塊用來提供自然圖像先驗，給融合圖像提供較好的視覺效果。EM模塊通過似然來保護源圖像的更多信息，用于對UDS輸出進行矯正。

EM模塊用來將f~0|t更新為f^0|t，在上圖算法中對應藍色和黃色部分。使用DDPM采樣（第五行）得到的f~0|t作為EM的起始輸入，獲得f^0|t（第6到13行），是經過似然校正的融合圖像的估計。總體來說，EM模塊就是將f~0|t更新為f^0|t來滿足似然。

為什么單步EM可以work：本文DDFM和傳統EM算法最大不同就是傳統方法需要多部迭代來獲得x，也就是上圖算法中的第6到13行需要多次循環。本文的DDFM只需要單階段EM迭代，可以直接嵌入到DDPM框架中完成采樣。下面給出命題3來解釋這種合理性。

命題3：單步無條件擴散采樣結合了單步EM迭代等價于單步有條件擴散采樣。下面是證明過程結論。

也就是說，條件采樣可以被分為無條件擴散采樣和單步EM算法，這就對應了本文的UDS模塊和EM模塊。

實驗部分

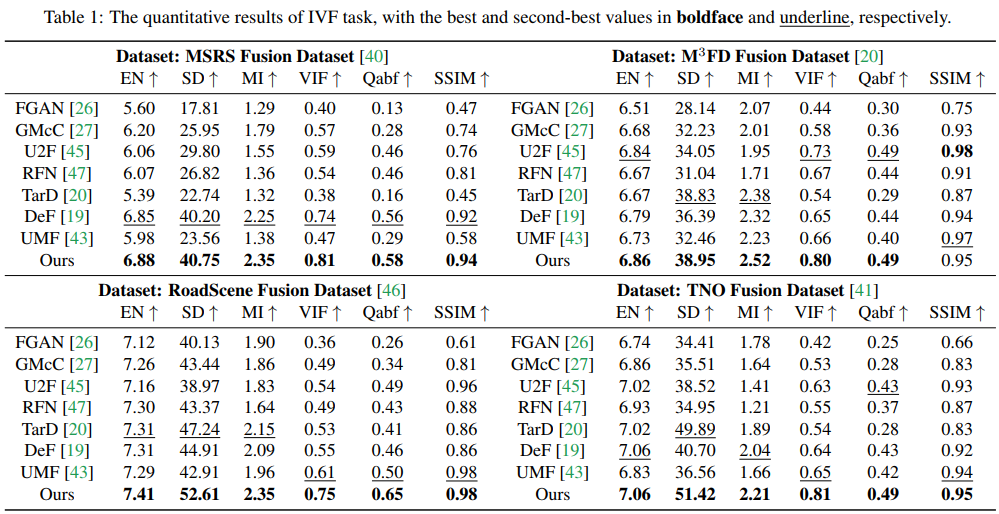
首先是IVF的實驗結果。實驗在TNO、RoadScene、MSRS、M3FD四個數據集上進行驗證，需要注意的是由于本文方法不需要針對特定任務進行fine-tune，所以不需要訓練集，直接使用預訓練過的DDPM方法即可。本文采用的是在imagenet上預訓練的模型。對比實驗結果如下。

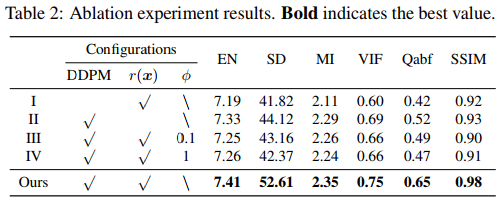
消融實驗一個針對UDS模塊，一個針對EM模塊。對于UDS模塊，去掉去噪擴散生成網絡，只用EM算法來解決式8的優化問題來獲得融合結果（實驗I）。為了公平對比，將總體的迭代次數設置的和DDFM相同。EM模塊是去除了式13中的總變分懲罰項，然后再去除貝葉斯推理模型（實驗II）。而前文也說過式8中的參數?可以在分層貝葉斯模型中推理，因此這里將參數?分別設置為0.1和1（實驗III和IV），使用ADMM來推理模型。以上設置的實驗結果如下表。

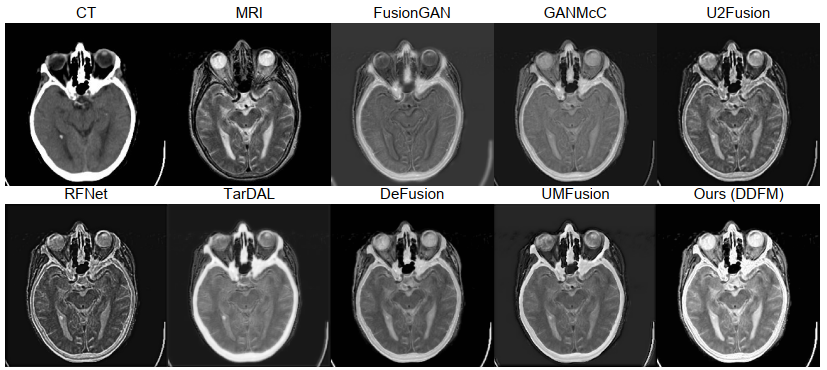
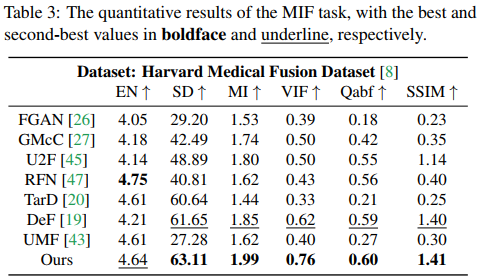
下一組實驗是醫學影像融合的結果，在 Harvard Medical Image Dataset 上進行測試，包含MRI-CT、MRI-PET、MRI-SPECT三種，實驗結果如下圖。