調制(Modulation)、包絡分析(Envelope)
如果噪聲中出現了明顯的調幅(AM)現象,BK Connect軟件還提供包絡分析(Envelope)。包絡分析能夠將調制信號從載波信號中分離出來。如下圖所示,紅色為載波信號,黑色為調制信號,經過包絡分析后,即可得到右下角的調制頻率fm。
包絡分析除了用于調制信號的解調分析以外,還適用于電機軸承的故障檢測,能從軸承振動噪聲信號中識別出微弱的故障信號,在出現故障的早期階段即能發現故障。
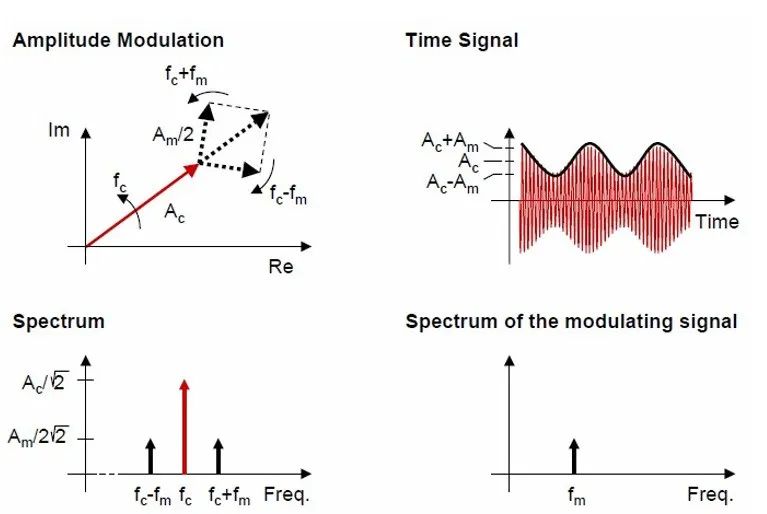
如下圖右圖的例子中,對載波所在頻段(125±100Hz)進行帶通濾波后,對包絡線時間歷程曲線進行FFT分析。Y軸幅值為包絡線的頻譜幅值。在頻譜中發現了明顯的峰值,說明信號中存在調幅現象。在噪聲信號的FFT分析結果中,如下圖左圖所示,我們發現在126Hz和120Hz有相鄰的峰值,其中幅值更高的126Hz為載波頻率,幅值較低的120Hz為調制信號頻率。根據調制信號幅值和載波信號幅值的比值,可計算出調制度(Degree of Modulation),為0.082/0.395≈21%。

如果在分析之前,無法確定載波頻率的頻率范圍,則可以先進行不同頻段的包絡分析,調查這些頻段的數據中,是否存在調制。如下圖例子所示,X軸橫坐標為調制頻率,左側Y軸縱坐標為包絡分析的載波頻帶中心頻率,Z軸顏色坐標為調制信號幅值。從圖中可以發現2500Hz載波頻帶和80Hz調制頻率處有明顯峰值(圖中黃色圓圈位置),同時在其他載波頻帶,如500Hz處,也存在多個調制頻率的峰值(圖中橙色圓圈位置),說明這些位置存在明顯的調制現象。

***純音比(Tone-to-noise Ratio)、突出比 ***
(ProminenceRatio)、音調(Tonality)
由于電機和傳動機構的結構特點,旋轉機構經常發出一些純音。這些純音可能讓電機噪聲聽起來尖銳刺耳、不和諧,令人煩躁。在分析純音問題時,需要考慮寬頻信號的掩蔽效應。當一個寬頻信號中存在一個純音時,純音的聲壓級幅值超過純音所在臨界頻帶聲壓級幅值6個dB以上,人耳才能聽到這個純音。
如果小于6dB,則人耳聽不到這個純音,它被周圍頻帶的寬頻聲音所掩蔽。下圖為純音比和突出比的圖例和定義。針對人耳的這種特性,BK Connect軟件提供了多種純音分析參數,包括純音比(Tone-to-noise Ratio) 、突出比(Prominence Ratio)和音調(Tonality),這些參數能自動判斷噪聲中是否存在明顯的純音。

FFT、1/3倍頻程(1/3 Octave)、
臨界頻帶(Critical Band)
FFT和1/3倍頻程多用于表述聲音能量在頻域上的分布。它們的縱坐標為聲音幅值,比如聲壓級dB、A計權聲壓級dB(A)等,橫坐標為頻率。FFT和1/3倍頻程最明顯區別之一是頻率坐標的分辨率。FFT的頻率分辨率在各個頻率都是一致的(如下圖左圖),而1/3倍頻程的頻率分辨率是中心頻率的固定百分比(約23%),頻率越低,每個柱狀圖代表的頻段越窄,也就是頻率分辨率越小,反之頻率越高,頻帶越寬,頻率分辨率越大(如下圖中圖)。
FFT和1/3倍頻程的本質區別是噪聲幅值的計算方法,FFT利用傅里葉變換原理,進行時域頻域轉換,得到各頻率的噪聲幅值。1/3倍頻程采用時域濾波器的方法,對時域信號進行帶通濾波,得到各頻段噪聲幅值。
FFT和1/3倍頻程主要表述聲音的能量分布,沒有考慮心理聲學中的頻域掩蔽效應,因此與人對聲音的主觀感受存在一定的差距。為了減少這種差距,在進行心理聲學分析時,通常使用臨界頻帶(單位bark)表述不同頻率的噪聲,臨界頻帶將人耳可聽頻段分為0-24bark(如下圖右圖)。

更多參數
如果噪聲信號具有非穩態特性,甚至是瞬態特性,除了上述常見的參數以外,還經常使用其他一些參數。他們由常規參數衍生出來的,這些參數也常用于評價電動零部件的異響。
百分位數
在研究噪聲問題時,噪聲中除了與自身形成機理有關的特征成分以外,還經常包含隨機成分,這使得噪聲數據經常分布在一定數值范圍內。為了方便量化噪聲數據的分布特性,引入統計學的一些方法,比如百分位數,常見的百分位數有第1、第50(也稱為中位數)、第99百分位數等。
以連續重復測試的三組數據為例,在下圖的響度時間歷程中,由于被測物運行狀態等因素的影響,無法保證三組數據的最大值是最穩定的、一致的。表格中為三組數據的第0至第15百分位數匯總,其中第0百分位數(第三行,即響度最大值)標準差為0.33Sone,而第3、4百分位數(第四、五行)標準差均明顯小于第0百分位數的標準差,因此第3、4百分位數具有更高的一致性。


(特征響度積分面積)百分位頻率
使用臨界頻帶表述不同頻率的響度時,我們將結果稱為特征響度,如下圖結果,橫坐標為臨界頻帶(bark),縱坐標為響度。在研究噪聲的頻域分布特性時,可以利用特征響度曲線計算出積分面積。
再利用積分面積百分位數所對應的頻率,來表述頻譜分布特性。百分位數的結果為特征頻率,單位Bark。以下圖為例,左右兩圖為兩個不同聲音的特征響度數據,兩個聲音的總響度分別為13.00 Sone和12.74 Sone,比較接近,但是它們的頻譜分布是不同的,例如,在9 Bark附近,左圖數值小于右圖,而在16.5 Bark附近,左圖數值大于右圖。以第50百分位頻率為例,低于某個特征頻率的積分面積,占總積分面積的50%,也可以描述為,某個臨界頻帶以上和以下特征頻率積分面積相等,即特征響度“重心”,此臨界頻帶對應的特征頻率即為第50百分位頻率。
在上述兩組數據中,左右兩圖的第50百分位頻率分別為12.5 Bark和11 Bark(圖中紅色豎線),這意味著左圖的特征響度“重心”比右圖更偏右說明特征響度主要集中在較高頻段。除了使用第50百分位頻率以外,也可以使用其他百分位數(比如第70百分位數)表示特征響度的分布特性。

對于瞬態噪聲信號,在瞬態噪聲的時間歷程中,頻率分布是隨時間變化的。以電機停止運行時的特征響度時域歷程為例,如下圖左側圖形所示,在0.09-0.25秒(藍框內的時間范圍)出現瞬態沖擊噪聲,在不同時刻下,特征響度是不同的。利用各個時刻的特征響度計算出百分位頻率,從而反映出各個時刻的頻率分布變化趨勢。下圖右側圖形為第70百分位頻率的時間歷程,其中的0秒為沖擊噪聲的峰值時刻,作為起始時刻。第70百分位頻率曲線隨時間逐步降低,意味著特征響度中的頻率成分,隨著時間逐漸向更低頻率轉移。

顫聲(Warble)
當電機處于勻速運行時,由于負載或阻力的影響,容易引起噪聲的低頻顫動,如下圖所示,在響度時間歷程數據中,從2.4秒至5.1秒(藍框內),響度值出現了明顯的低頻顫動。如果此類顫動的頻率在2-8Hz(也有文獻規定為1-10Hz)時,通常將之稱為顫音(Warble)。下圖的顫音現象中,包含了多個周期的極大值和極小值,如圖所示的6個周期的極值。

-
調制解調器
+關注
關注
3文章
857瀏覽量
38876 -
帶通濾波器
+關注
關注
18文章
228瀏覽量
43215 -
FFT變換
+關注
關注
2文章
10瀏覽量
8798 -
頻譜儀
+關注
關注
7文章
342瀏覽量
36150 -
電機軸承
+關注
關注
1文章
48瀏覽量
4210
發布評論請先 登錄
相關推薦

2011第九屆廣州車展|汽車零部件及用品展
沖模的零部件組成
請教測試一個汽車零部件問題
RFID的航空零部件追蹤
汽車零部件尺寸全檢測量方案
圖像尺寸測量儀:解析適用零部件與應用領域
機械設計中標準零部件的應用
風電機組各零部件進行風險評估的一個示例

德爾福的新工廠將專門生產電動車電子零部件
汽車零部件行業概況
虹科方案|LIN/CAN總線汽車零部件測試方案
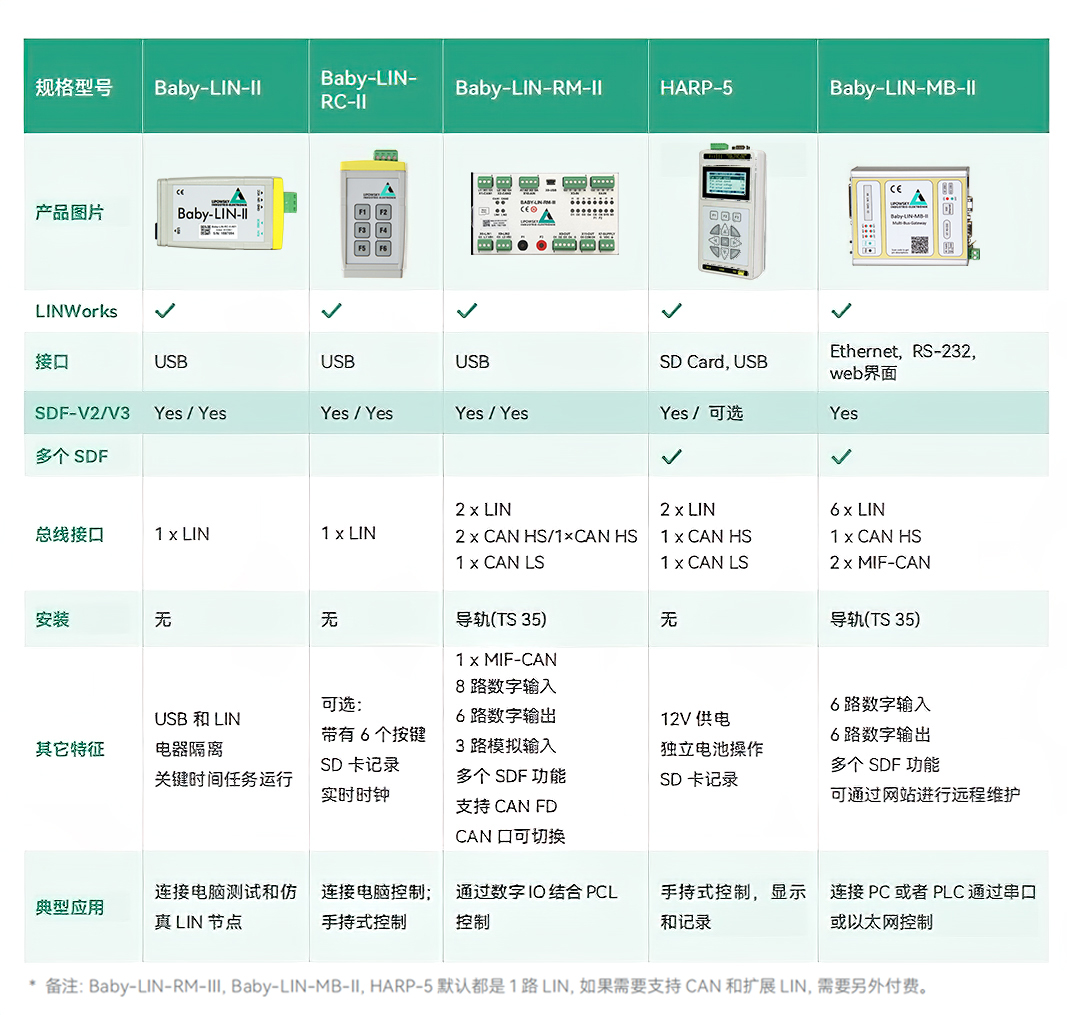




 電動零部件異響分析參數方案(一)
電動零部件異響分析參數方案(一)










評論