理論分析

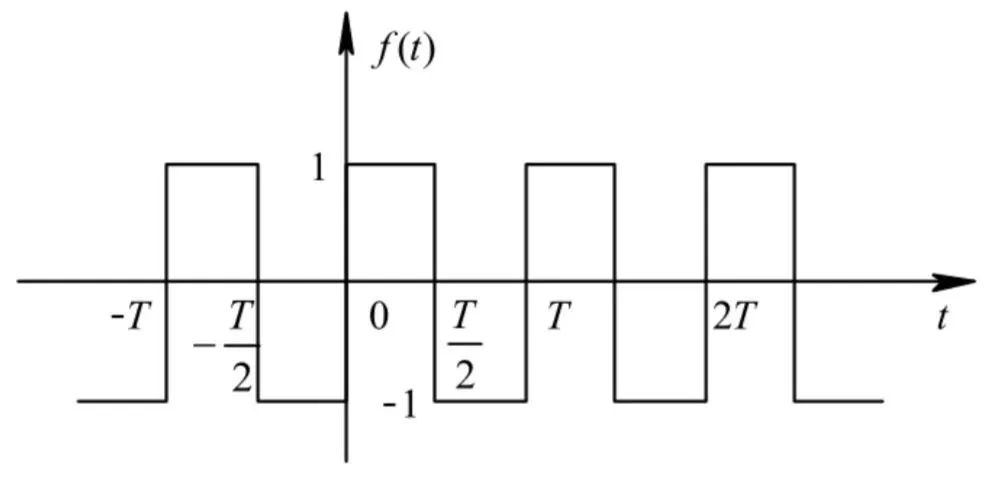
傅里葉變換中提到：任意波形均可分解為無數不同幅值和頻率的正弦波的疊加。那么以最常見的方波(在工作中是以時鐘信號，PWM信號等等出現)為分析對象，幅值為1，頻率為1/T的方波波形，如下圖所示：

通過傅里葉變換后，方波公式可以列為：

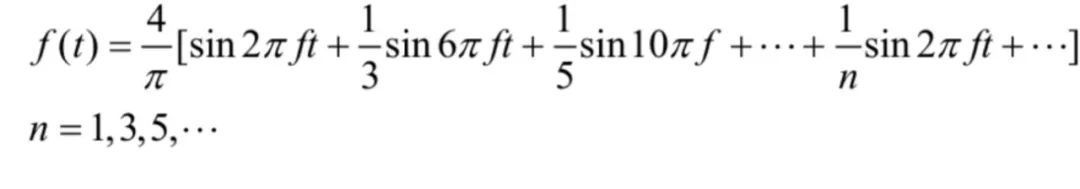
上式的意思是：

方波可以分解為頻率為 f 赫茲(f=1/T)幅值為

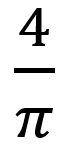
的正弦波，加上頻率為 3*f 幅值為

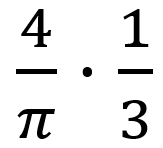
的正弦波，再加上頻率為5*f幅值為

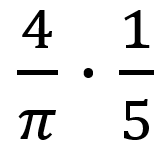
的正弦波，以此類推無數正弦波的疊加。

仿真驗證

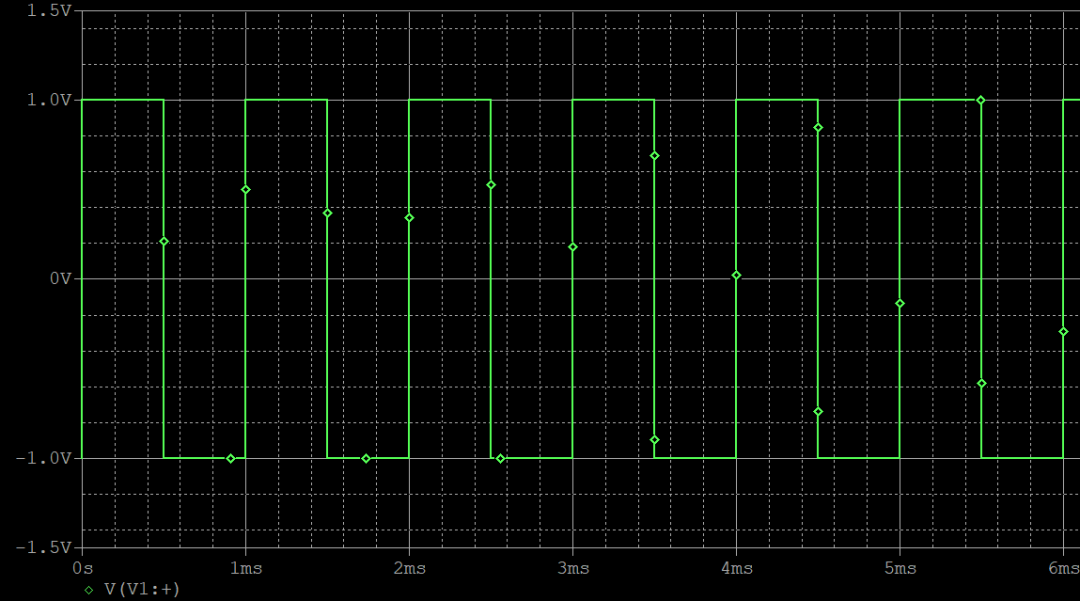
那么就開始做一下仿真驗證一下，首先用PSpice輸出一個頻率為1kHz，幅值為1V的方波。時域波形如下所示：

對波形進行傅里葉變換后，轉化為頻域，波形如下圖所示：

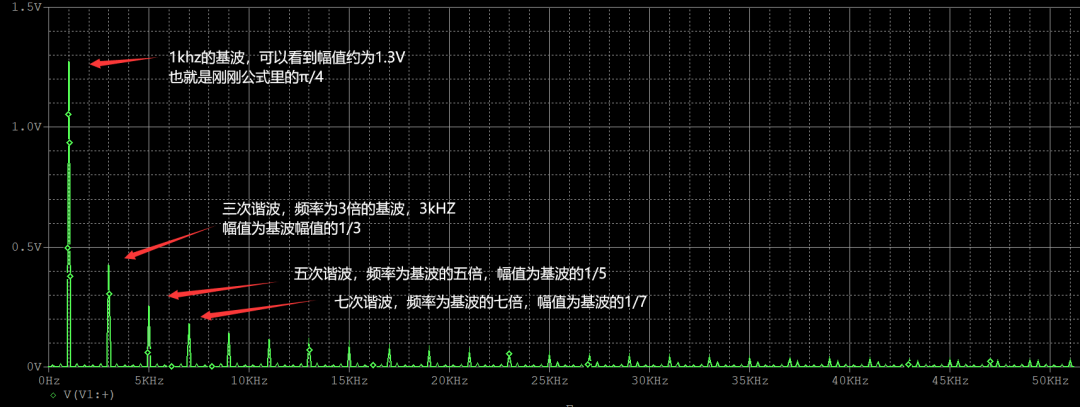
從頻域圖中，可以發現，基波頻率和方波頻率相同，基波的幅值為方波幅值的

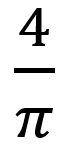
倍，這些也均和之前得到的公式中分析的一樣，X次諧波頻率為基波的X倍，幅值為基波的1/X;諧波的幅值會隨諧波頻率的增加而減小。

那么頻域的分解我們得到了，是不是可以反推回去呢?這個我就直接找了一個multisim的仿真圖(書內帶的仿真，回復：模擬電子技術基礎，獲得書以及配套書的所有仿真，方便理解強烈推薦!!)，圖為通過反相加法器，將不同頻率的正弦波疊加到一起(不同頻率有不同權重，三次諧波放大倍數為

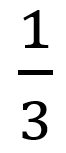
，五次諧波放大倍數為

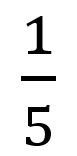
，以此類推)。正弦波1kHZ基波幅值設置

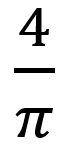
V，約等于1.2732V。那么只看基波的波形是這樣的：

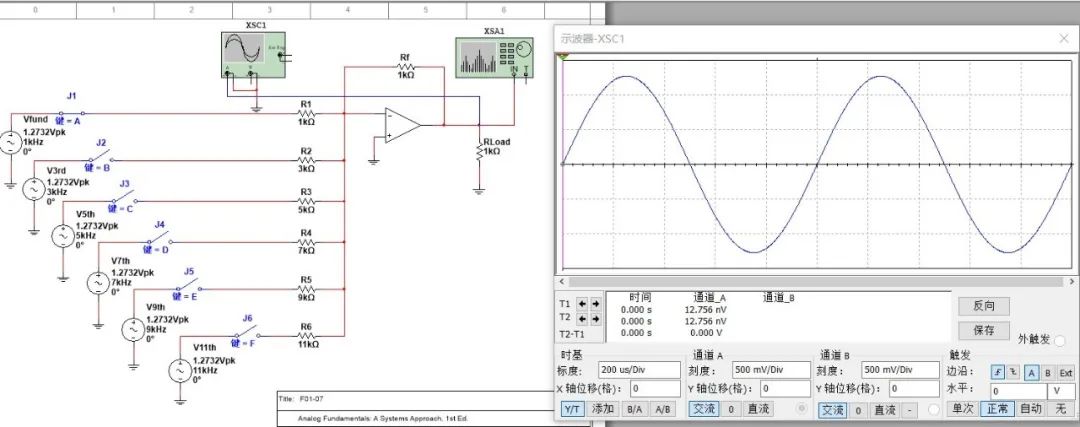
基波+三次諧波：

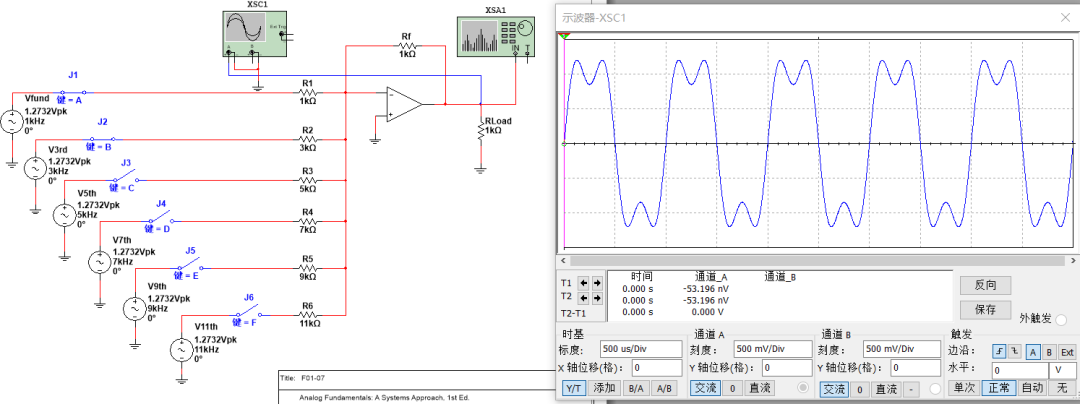
基波+三次諧波+五次諧波，是不是已經看到方波的樣子了：

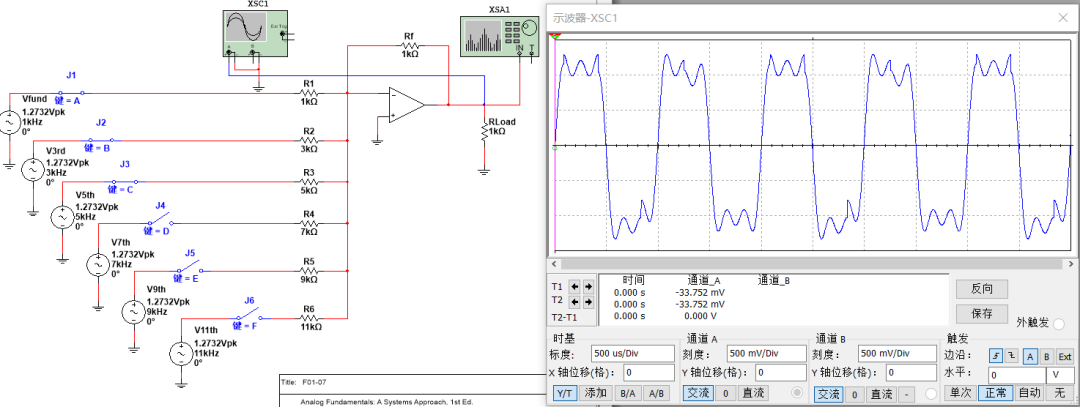
基波+三次諧波+五次諧波+七次諧波，是不是更像方波了：

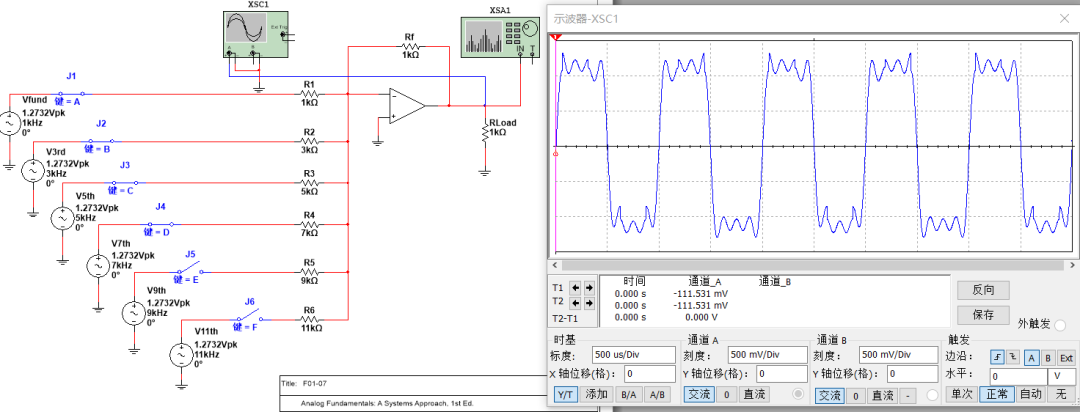
基波+三次諧波+五次諧波+七次諧波+九次諧波+十一次諧波：

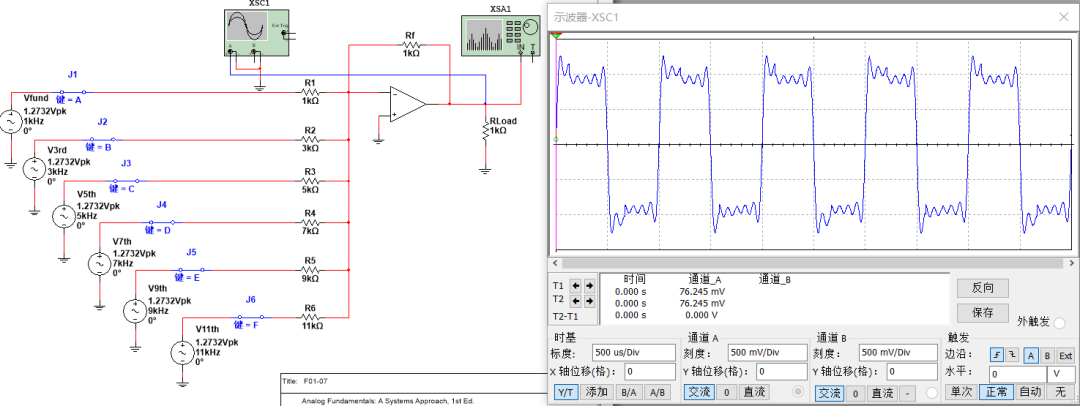
由于篇幅的關系，只疊加到了十一次諧波，不過看幅值已經很接近幅值為1V頻率為1kHz的方波了!!

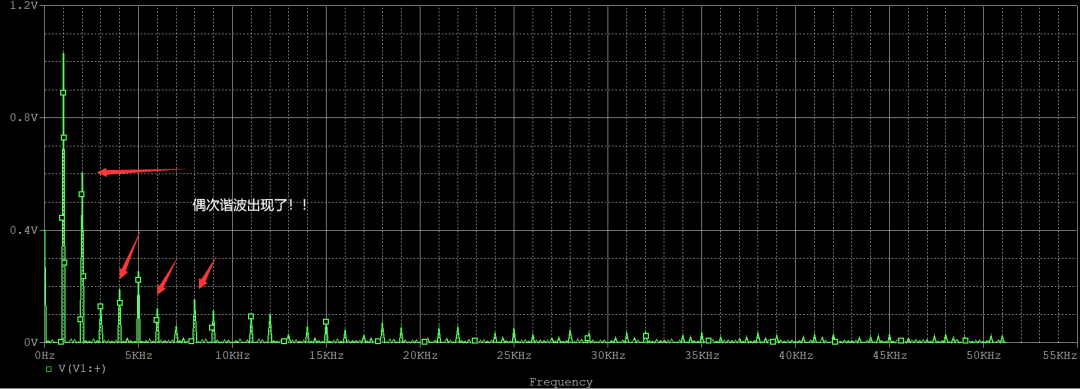
不過這時，不知您是否心中會閃過一絲疑問：為什么只有奇次諧波，沒有看到偶次諧波??那么在這里只提一個結論，推導過程就不列在本文了。

結論是：占空比為50%的方波沒有偶次諧波。只有占空比不是50%的方波才有偶次諧波。(所以大多數可以看到的諧波是奇次諧波)

那么就繼續用PSpice驗證這一結論，在原來波形的基礎上將占空比從50%修改到70%，1kHz頻率和1V幅值保持不變。時域波形如下所示：

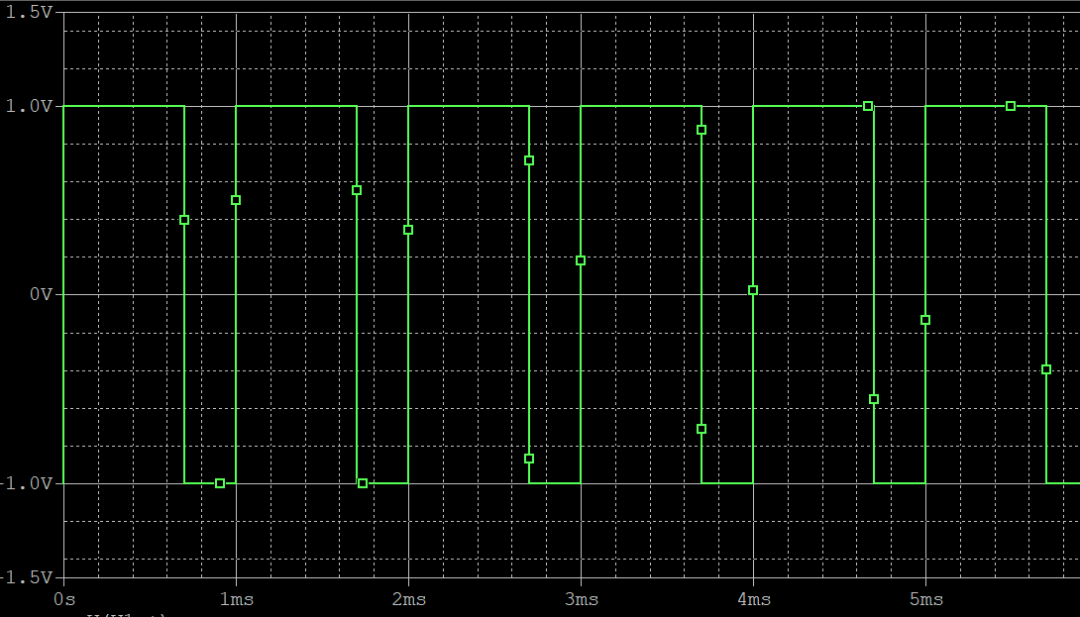
對其進行傅里葉變換，轉化到頻域，波形如下，偶次諧波出現了!!

最后說兩句

那么讀到這里，是不是您的心里是不是已經明白示波器的帶寬為什么這么重要了呢?如果您的示波器帶寬太小，或者您在測量高速信號(比如10Mhz或者更高)的時候無意間打開了帶寬限制，那么方波的高次諧波就被濾掉啦哈哈。

所以您觀察到的方波就變形了，就失真了，就像用multisim仿真的那個只疊加到十一次諧波的方波一樣，出現了失真!!

同理可推運算放大器的帶寬(要放大方波信號的時候要考慮其高次諧波，不能僅僅只看基波的頻率)。