同態加密是一種支持數據密態處理的密碼學技術,可以廣泛應用于云計算、醫療、金融等領域。
一、什么是同態加密
全同態加密是一種加密技術,允許在不解密的前提下,對密文進行一些有意義的運算,使得解密后的結果與在明文上做 “相同計算” 得到的結果相同。
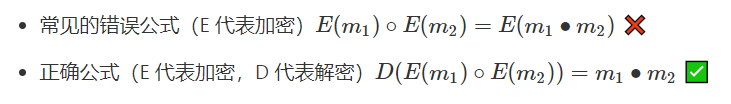
通常所說的 “同態加法”,“同態乘法”,指的是明文上的運算,即 對應的運算
同態加密被稱為密碼學的 “圣杯”,原因是同態加密算法功能十分強大,可以支持密文上的任意操作。
目前的全同態加密算法效率比較低,只能支持一些簡單的代數或邏輯運算,對一些復雜的計算邏輯支持較差。
二、理論到實現
2.1 理論
全同態加密的思想早在 1978 年由 Rivest,Adleman 和 Dertouzos(前兩位就是 RSA 中的 R 和 A)在他們的論文《On Data Banks and Privacy Homomorphisms》中提出。論文中提出了對密文進行一定的計算,可以間接地對原文進行操作的構想。需要指出的是,這離公鑰密碼學概念的提出,才僅過去兩年的時間,由此也凸顯了密碼大牛的想象力和洞見力。后來,這種技術才被重新命名為同態加密。
傳統的一些密碼方案具有一些簡單的同態性質,如教科書式的 RSA 算法(支持同態乘法),Paillier 算法(支持同態加法)等。然而,這些算法離真正的全同態加密還有很大的距離。
2.2 方案
經過 30 多年的發展,Gentry在其博士論文中提出了第一個真正意義上的全同態加密方案。該方案基于理想格,利用環結構上的同態性質設計。
全同態加密方案:
簡單來說,假如I?RI?R是環RR的一個理想,x∈Rx∈R是環中的任意一個元素,則xI?IxI?I(吸收律),I+I=II+I=I(封閉性)。考慮商環R/IR/I。對于任意的x,y∈R,x,y∈R,有
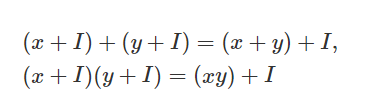
這些就是商環的運算性質,而性質恰好可以用來構造同態加密。不嚴格地講,如果把 運算想象成 “加密” 過程,上面實際上可以翻譯為:
“xx的密文” 與 “yy的密文” 經過 “加法” 運算 ===》“x+yx+y的密文”
“xx的密文” 與 “yy的密文” 經過 “乘法” 運算 ===》 “xyxy的密文”
這正是同態加密所要完成的功能!
然而需要指出的是,這種方案還是只能支持有限次的同態乘法和同態加法,離 “任意運算” 還是有不小的距離,所以仍然不是一個真正的全同態加密方案。因為上述由理想格設計出的方案本質上是基于噪聲的,運算過程中噪聲的規模會增長。當噪聲增長到一定程度后,就不能從密文中將信息恢復出來了。Gentry 將這類可以支持一定程度上的同態加法和同態乘法的加密方案稱為 “SomeWhat Homomorphic Encryption” (簡稱為 SHE 或 SWHE) 。
在 Gentry 之前僅有的類似方案是 05 年提出的 BGN 方案。其基于橢圓曲線上的雙線性對構造,可以支持同態加法和一次同態乘法因此,為了實現真正意義上的全同態加密,Gentry并沒有停下前進的腳步。
Gentry 的另一個貢獻,也是構造全同態加密的關鍵,那就是提出了 Bootstrapping 技術:通過同態執行解密電路(即始終保持在密文狀態下執行解密電路),對密文進行刷新,將其中所含的噪聲減少,使其能夠再進行同態乘法和同態加法運算。通過重復執行 Bootstrapping, 便可以將 SWHE 方案轉化為 FHE 方案。這就是 Gentry 提出的構造全同態加密的藍圖,也是目前唯一已知的構造全同態加密的方式。
這里有一個比較有意思的點。前面說了 ,SWHE 只能支持有限次的同態乘法操作,而 Bootstrapping 中需要同態執行解密電路,那么一個很顯然的推論就是,解密電路中需要執行的乘法運算不能超過 SWHE 中能支持的同態乘法的界限,因為需要在 SWHE 中實現 Bootstrapping 操作。但是,通過分析發現,幾乎所有的可用的加密方案,執行其解密電路所需的乘法操作總是超過了 SWHE 中能支持的同態乘法的界限。
這個看似不可逾越的鴻溝,好像給Gentry的同態加密構造藍圖打上了 “不可能” 的標簽。但是 Gentry 通過引入一些新的計算假設,成功地將解密電路中所需的乘法操作拉到 SWHE 能支持的乘法操作范圍內。從而成功地構造出了第一個全同態加密方案。
三、全同態加密發展歷程
此后的第二代(BGV 等方案為代表)、第三代(GSW 方案為代表)全同態加密方案中,都有 Gentry 的貢獻。可以毫不夸張地說是Gentry大神敲開了全同態體系的大門,并在隨后的 14 年中不斷地推動「同態加密算法」的發展。由于在同態加密領域的杰出工作,Gentry 獲得了 2022 年的哥德爾獎。有人預測,一旦同態加密獲得大規模應用,Gentry很可能獲得圖靈獎。
花邊新聞:Gentry 在哈佛獲得法學學位后,曾做過一段時間律師。令人津津樂道的跨界成功的教科書式案例,“出道即巔峰” 的典型代表。
從 Gentry 提出第一個全同態加密方案開始,全同態加密算法在設計、分析、優化、實現、應用等研究方向上都取得了很大的進展。而全同態加密算法本身也經歷了輪的 “迭代升級”。
(關于下面的分代,學術界也存在一些爭議。這里給出其中一種便于我們描述的分代方式,不代表小編的觀點)
| 第一代 | 主要是以 Gentry 基于理想格的方案和 van Dijk 等基于整數環上的 AGCD 困難性的 DGHV 方案為代表。Gentry 的方案涉及了較多的代數數論,方案有些復雜。而 DGHV 方案基于整數,方案簡單,便于理解,但計算復雜度高,公鑰尺寸非常大,很不實用 |
| 第二代 | 以 Brakerski 和 Vaikuntanathan 等人基于 LWE 問題等設計的 BV 方案為起點,代表性的有 BGV 方案和 BFV 方案。這一類方案主要以層次型(leveled FHE)結構為主,針對一些特定的場景,通過精心設計參數,可以避免在計算過程中引入耗時的 Bootstrapping 操作。此外,同一時間內,López-Alt 等人還基于 NTRU(一個格密碼方案)提出了一種稱為多密鑰 FHE 的同態加密方案的概念,支持對不同密鑰加密的密文進行計算。進一步提升了同態加密的功能性,擴展了其在實際中的使用范圍 |
| 第三代 | 以 Gentry 等人(GSW)方案為開端。GSW 方案基于近似特征向量構造,設計了一種不同的方法來執行同態運算。該方案一個非常有意思的點是可以用來構造屬性基(Attribute-Based)加密。現在一些高級的設計中,很多都以 GSW 方案為組件。與此同時,比較著名的代表方案還包括 FHEW 和 TFHE 等 |
| 第四代 | 以 CKKS 為主要代表。也有學者將其歸為第二代,與 BGV、BFV 方案等并列。嚴格來講,CKKS 并不是同態加密方案,而是近似同態加密方案。D(E(m1)°E(m2))≈m1?m2D(E(m1)°E(m2))≈m1?m2然而,由于其對浮點數的支持比較好。因此被廣泛使用在隱私保護機器學習等場景中。此外,Li 等人還對 CKKS 算法給出了攻擊和修復建議 |
| 發展歷程 | 同態加密方案 |
|---|
噪聲管理是目前全同態加密方案中的一個重要部分,很多方案論文中,考慮的關鍵點就是更好的噪聲管理方式。實際上,也出現過一些無噪聲的 “同態加密方案”,主要基于非交換代數設計,但是這類方案安全性很低,基本上每出現一個方案,很快就被攻破了。
審核編輯:劉清
-
芯片解密
+關注
關注
2文章
60瀏覽量
11658 -
機器學習
+關注
關注
66文章
8438瀏覽量
132928 -
同態加密
+關注
關注
1文章
5瀏覽量
1923
原文標題:同態加密為什么能被稱為密碼學的 “圣杯”?
文章出處:【微信號:OSC開源社區,微信公眾號:OSC開源社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
物聯網安全機制密碼學基礎
基于同態加密系統的圖像魯棒可逆水印算法
同態加密方案及安全兩點直線計算協議
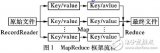
基于MapReduce計算框架的并行同態加密方案




 什么是同態加密?同態加密為什么能被稱為密碼學的圣杯?
什么是同態加密?同態加密為什么能被稱為密碼學的圣杯?











評論