問題的定義
這一次日篤小編來教大家如何在simulnk里面,求解偏微分方程(Partial Differential Equation-PDE)。這次給大家講解偏微分方程。跟ODE不同的是,PDE的變量不僅是時間的函數,而且也是空間的函數。舉個簡單的例子:炒菜的鍋的鍋壁溫度,溫度這個變量不僅僅是時間的參數(不同時候,鍋壁同一個點的溫度不一樣),而且也是空間的參數(同一時刻,鍋壁不同位置的溫度不一樣)。求解PDE的時候可以直接求解,也可以先轉化成ODE,再用求解ODE的方法求解。這里,小編先將PDE轉化成ODE再求解。
主要方程的定義
先給出三個相互關聯的方程(前兩個是PDE,第三個是ODE):
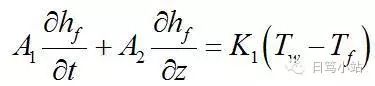
其中Tf是hf關系式,A和K是常數

其中Te是he關系式,A和K是常數
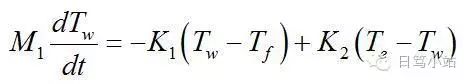
M和K是常數
PDE轉化為ODE
再將前面兩個PDE轉化為ODE:
這樣我們就得到了三個ODE,運用顯示的ODE求解方法,通過簡單的歐拉展開,我們可以得到三個變量的求解顯示表達式:
再將前面兩個PDE轉化為ODE:


這樣我們就得到了三個ODE,運用顯示的ODE求解方法,通過簡單的歐拉展開,我們可以得到三個變量的求解顯示表達式:
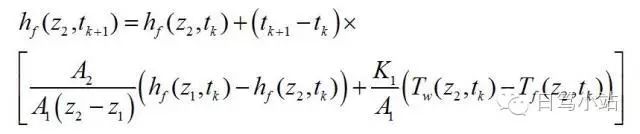

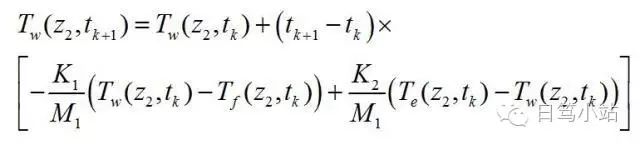
邊界條件和起始條件的討論和設定
這三個表達式中,只有等式左邊的參數是未知數,等式右邊的所有變量都是已知的。要求解這三個表達式,我們需要設定一些條件:起始條件和邊界條件。所謂起始條件就是開始模擬的那一個時刻,狀態量的數值,在這里我們需要給定Tw,hf,he三個變量在Z1,Z2位置對應的數值。如果模擬的持續時間很長,起始條件在一定范圍內一般對整個模擬的影響不是特別大,比如計算電池充放電過程中電池內部溫度的變化(一般持續10個小時以上);但是如果模擬持續時間短,起始條件的設定就顯得尤為重要,比如汽車碰撞(一般在0.5秒以內就能完成),或者安全氣囊的起爆過程(一般在0.015秒內就能完成)。邊界條件指的是有限元或者有限體積法將一個平面或者立體劃分成很多個小單元,這些單元在物理邊界的位置,狀態量隨時間變化的關系。比如:要計算一個炒菜鍋炒菜過程中鍋壁溫度的分布,我們需要知道鍋底火焰再各個接觸面的溫度隨時間變化的關系;再比如要計算一個輪胎的壓到一顆石子過程中的變形過程,我們需要知道這個石頭在輪胎表面產生的輪廓隨時間變化的關系;再比如我們要計算一個空調房各個角落的溫度,我們需要知道,空調出風口的風速大小方向、溫度、濕度隨時間變化的關系,以及房間門口地下縫隙跟室外空氣交換的速度以及室外空氣溫度和濕度隨時間變化的關系。
下面小編設定一下上面式子的起始條件(Initial Condition - I.C)和邊界條件(Boundary Condition - B.C):
I.C:
Tw = [377.540533331317 386.026288241315 394.882816943803 403.780234260442 412.528927823382 421.020618818433 429.194964414357 437.019737325395 444.479243081580 451.567215232647 458.281835132688 464.622699931517 464.045356725446 461.548572973745 460.533446196397 459.951339710425 459.573192331990 459.311655878501 459.125265766771 458.992877081766 458.900967710798 458.850165061973 458.921507977048 459.670267128948 488.518351484883 503.038359452690 516.356161826663 528.545395038828 539.687125046220 549.862685009442]
hf = [335879.230662688 383800.108882945 430054.713708057 474539.317712384 517232.789150323 558163.101428462 597387.616256567 634981.549133264 671031.215823456 705630.227842953 738877.802385151 770878.391400899 804774.697027078 841552.709305229 880672.392971595 922052.212463106 965712.639000156 1011715.66565823 1060145.65583764 1111101.06457330 1164632.21059020 1220683.53929694 1279315.98281919 1340335.98261620 1390832.64999538 1436955.33525927 1479057.18575508 1517473.69348631 1552518.42857505 1584481.89301558]
he = [502113.781884773 508072.678267337 513859.836263859 519445.766992407 524817.943825280 529973.814790241 534916.758091738 539653.701008431 544193.726929246 548547.259765169 552725.604497504 556740.743076404 560605.289626758 564698.772122112 569140.263508662 573864.546505107 578861.774480850 584134.419639887 589689.968567105 595538.609396464 601692.232036153 608156.913219795 614925.943905113 622006.682551548 629375.754089632 635473.976895104 641043.976376731 646128.400323336 650767.764378679 654999.936793652]
B.C :

Simulink建模
上述三個方程式代表的是有限體積法中一個小單元的方程,小編把很多個小單元依次連接起來,重復求解上述方程就能夠得到解。對于有限體積法,在方程求解器設計的過程中,一開始并不知道需要離散多精密才能得到理想的解的精度,所以一開始不知道要求解多少組這樣的三個方程。如果把一組三個方程的求解寫在一個simulink的block里面,如果要用100組的話,小編需要復制粘貼100次,不是很顯示,并且連線都會連得手抽筋,小編選擇用simulink里面的matlab function模塊,這個模塊就是把matlab的m文件與simulink對接起來,能夠用m文件最大的好處就是可以寫for循環,這樣的話,只需要改變for循環的循環次數,就能夠很容易的實現不同離散程度方程的求解。下面小編把最終的simulink文件的截圖奉上:

起始條件是放在simulink的記憶block里面:


而邊界條件則通過查表的方式,實時輸入到matlab function里面,這里只需要事先把隨時間變化的邊界條件存成一個隨時間變化的一維向量,保證時間向量的長度跟邊界條件向量的長度保持一致就行,然后利用simulink的1D(一維)表格,輸入是時間,輸出是對應的邊界條件(如下):


然后就設定模擬時間,在simulink的設置里面,選定離散的一階歐拉求解器,就可以開始模擬了。
Simulink仿真結果
下面給出三個狀態變量隨時間變化的曲線:



-
MATLAB仿真
+關注
關注
4文章
176瀏覽量
19968 -
simulink仿真
+關注
關注
0文章
75瀏覽量
8590
發布評論請先 登錄
相關推薦




 Matlab/Simulink建模詳解:一階時變偏微分方程的求解
Matlab/Simulink建模詳解:一階時變偏微分方程的求解










評論