連續模型是指模型是連續函數的一類模型總稱,具體建模方法主要是微分方程建模。微分方程建模是數學建模的重要方法,因為許多實際問題的數學描述將導致求解微分方程的定解問題。把形形色色的實際問題化成微分方程的定解問題,大體上可以按以下幾步:
1.根據實際要求確定要研究的量(自變量、未知函數、必要的參數等)并確定坐標系。
2.找出這些量所滿足的基本規律(物理的、幾何的、化學的或生物學的等等)。
3.運用這些規律列出方程和定解條件。
MATLAB 在微分模型建模過程中的主要作用是求解微分方程的解析解, 將微分方程轉化為一般的函數形式。 另外, 微分方程建模, 一定要做數值模擬, 即根據方程的表達形式, 給出變量間關系的圖形, 做數值模擬也需要用 MATLAB 來實現。
微分方程的形式多樣,微分方程的求解也是根據不同的形式采用不同的方法, 在建模比賽中, 常用的方法有三種:
1.用 dsolve 求解常見的微分方程解析解
2.用 ODE 家族的求解器求解數值解
3.使用專用的求解器求解
1.常規微分方程的求解
微分方程在 MATLAB 中固定的表達方式, 這些基本的表達方式如下表所示:
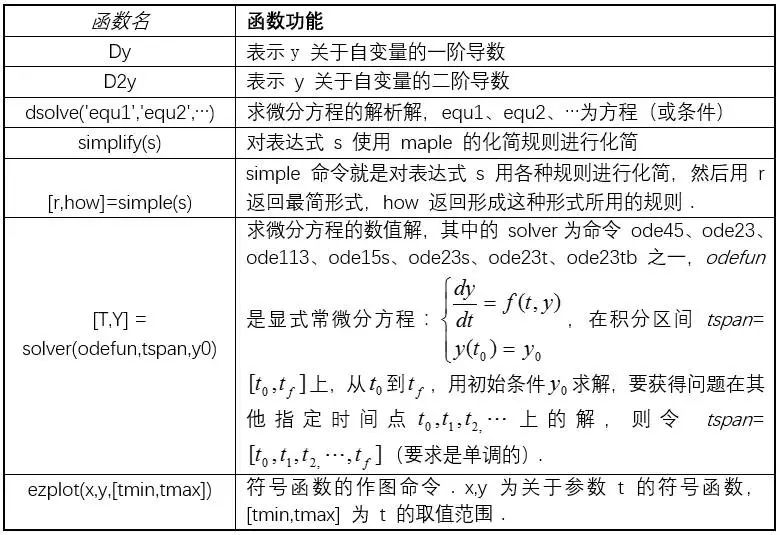
對于通常的微分方程, 一般需要先求解析解, 那么 dsolve 是首先考慮的求解器,因為dsolve 能夠求解解析解,其具體的用法如下:
[實例]求微分方程 xy'+y-e^x=0 在初始條件 y(1)=2e 下的特解,并畫出解函數的圖形.
求解本問題的 Matlab 程序為:
syms x y
y=dsolve('x*Dy+y-exp(x)=0','y(1)=2*exp(1)','x')
ezplot(y)
微分方程的特解為:y=1/x*exp(x)+1/x*exp (1) (Matlab格式),即 y=(e+e^x)/x ,此函數的圖形如圖 1:
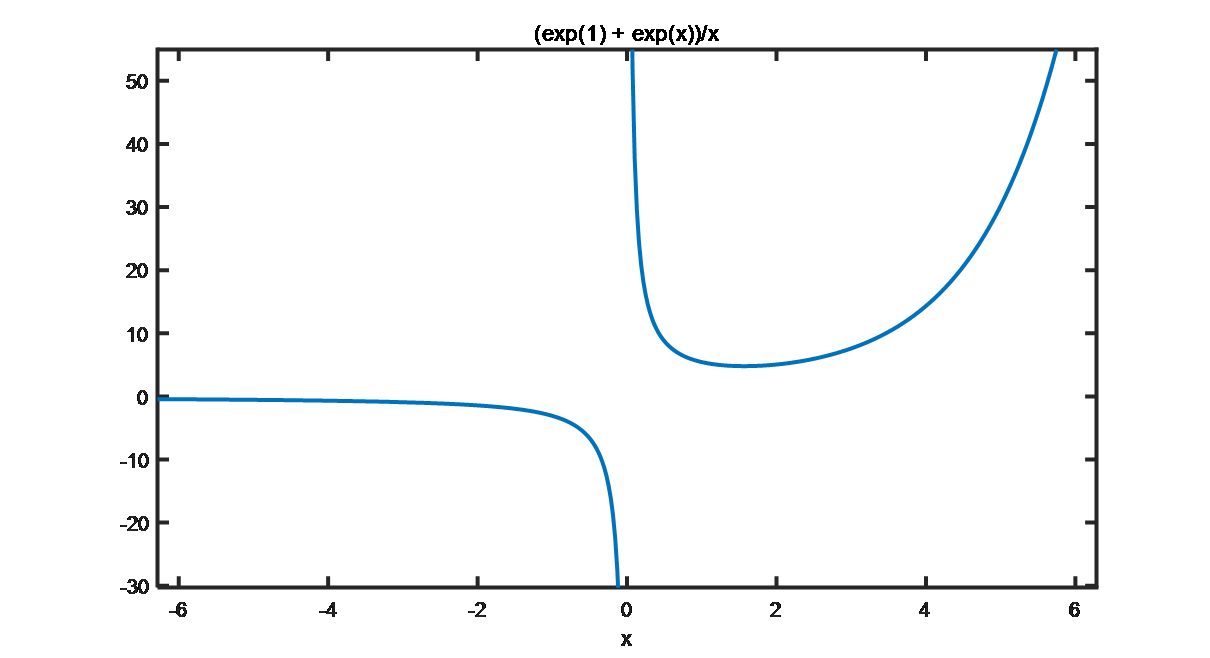
圖1y關于x的函數圖象
2.ODE 家族求解器
如果微分方程的解析形式求解不出來, 那么退而求其次的辦法是求解數值解,那么這個時候就需要用 ODE 家族的求解器求解微分方程的數值解啦。
因為沒有一種算法可以有效地解決所有的 ODE 問題,為此,MATLAB 提供了多種求解器,對于不同的 ODE 問題,采用不同的 Solver。MATLAB 中常用的微分方程數值解的求解器及特點如下表所示。
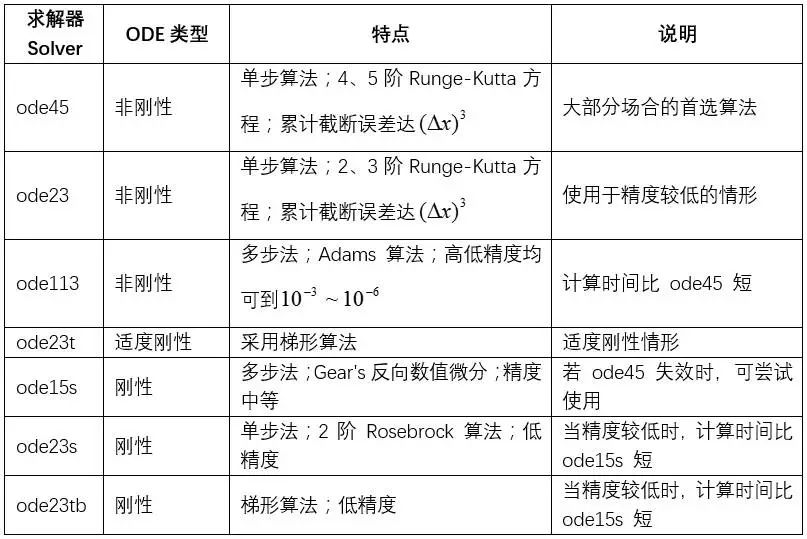
要特別提醒的是:ode23、ode45 是極其常用的用來求解非剛性標準形式一階常微分方程(組)初值問題解的 Matlab 的常用程序,其中:
ode23 采用龍格-庫塔2 階算法,用3 階公式作誤差估計來調節步長,具有低等的精度.
ode45 則采用龍格-庫塔4 階算法,用5 階公式作誤差估計來調節步長,具有中等的精度.
[實例]導彈追蹤問題
設位于坐標原點的甲艦向位于 x 軸上點 A(1, 0) 處的乙艦發射導彈,導彈頭始終對準乙艦。如果乙艦以最大的速度v0(是常數)沿平行于 y 軸的直線行駛,導彈的速度是 5*v0,求導彈運行的曲線方程,以及乙艦行駛多遠時,導彈將它擊中?
記導彈的速度為 w,乙艦的速率恒為v0。設時刻 t乙艦的坐標為 (X(t),Y(t)),導彈的坐標為 (x(t),y(t))。當零時刻,(X(0),Y(0))=(1,0),(x(0),y(0))=(0,0),建立微分方程模型:
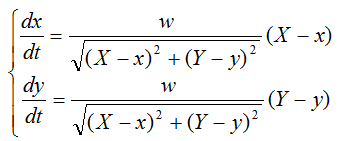
因乙艦以速度v0沿直線 x=1 運動,設v0=1,w=5,X=1,Y=t,因此導彈運動軌跡的參數方程為:
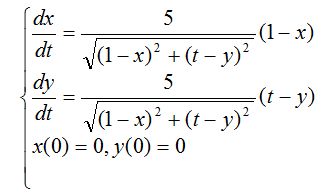
MATLAB 求解數值解程序如下:
(1)定義方程的函數形式:
function dy=eq2(t,y)
dy=zeros(2,1);
dy(1)=5*(1-y(1))/sqrt((1-y(1))^2+(t-y(2))^2);
dy(2)=5*(t-y(2))/sqrt((1-y(1))^2+(t-y(2))^2);
(2)求解微分方程的數值解
t0=0,tf=0.21;
[t,y]=ode45('eq2',[t0 tf],[0 0]);
X=1;Y=00.21;plot(X,Y,'-')
plot(y(:,1),y(:,2),'*'),hold on
x=01; y=-5*(1-x).^(4/5)/8+5*(1-x).^(6/5)/12+5/24;
plot(x,y,'r')
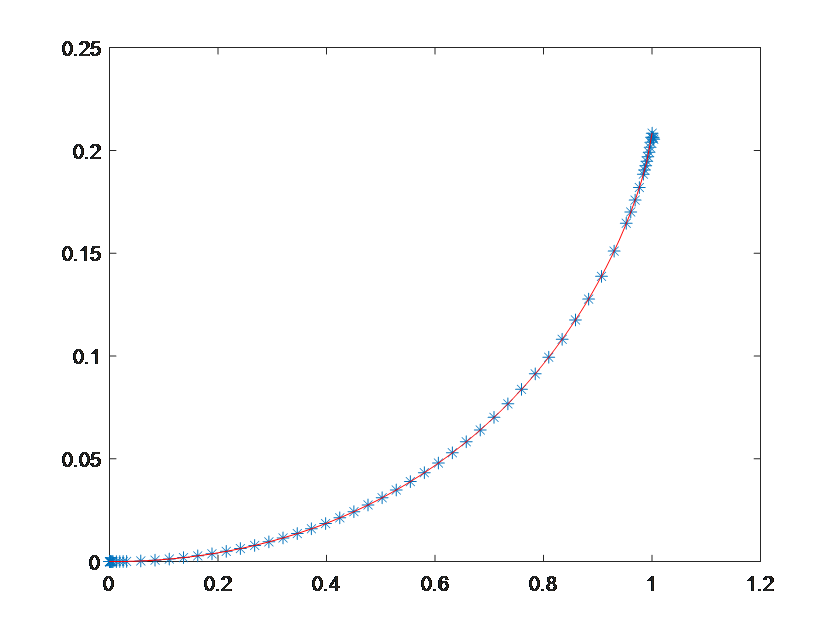
3.專用求解器
對于復雜的微分方程模型的求解, 可以借助 MATLAB 偏微分方程工具箱中的專用求解器。以下將以一個實例來看看如何借助偏微分方程工具箱來實現一個微分方程的求解與數值仿真。
所研究的對象是一個二階波的方程:

這個時候要查看一下 MALTAB 中哪個函數能求解相類似的方程, solvepde 可以求解的方程形式為:

可以發現只要通過參數設定就可以將所要求解的方程轉化成這種標準形式。
具體求解步驟如下:
(1) 設置參數
c = 1;
a = 0;
f = 0;
m = 1;
(2) 定義波的空間位置
numberOfPDE = 1;
model = createpde(numberOfPDE);
geometryFromEdges(model,@squareg);
pdegplot(model,'EdgeLabels','on');
ylim([-1.1 1.1]);
axis equal
title'Geometry With Edge Labels Displayed';
xlabel x
ylabel y
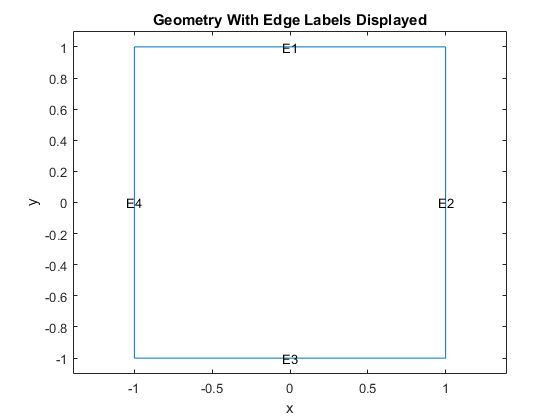
(3) 定義微分方程模型的系數和邊界條件
specifyCoefficients(model,'m',m,'d',0,'c',c,'a',a,'f',f);
applyBoundaryCondition(model,'dirichlet','Edge',[2,4],'u',0);
applyBoundaryCondition(model,'neumann','Edge',([1 3]),'g',0);
(4)定義該問題的有限元網格
generateMesh(model);
figure
pdemesh(model);
ylim([-1.1 1.1]);
axis equal
xlabel x
ylabel y
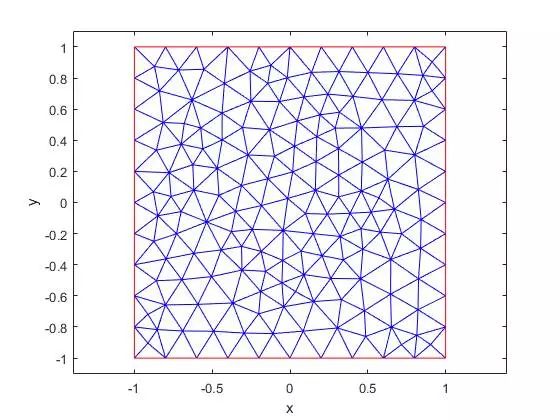
(5)定義初始條件
u0 = @(location) atan(cos(pi/2*location.x));
ut0 = @(location) 3*sin(pi*location.x).*exp(sin(pi/2*location.y));
setInitialConditions(model,u0,ut0);
(6)方程的求解
n = 31;% 求解次數
tlist = linspace(0,5,n);
model.SolverOptions.ReportStatistics ='on';
result = solvepde(model,tlist);
u = result.NodalSolution;
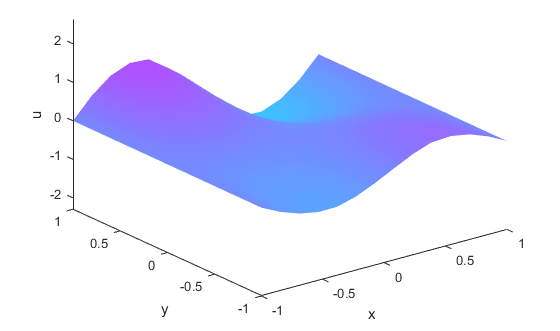
(7)模型的數值仿真
figure
umax = max(max(u));
umin = min(min(u));
for i = 1:n
pdeplot(model,'XYData',u(:,i),'ZData',u(:,i),'ZStyle','continuous',...
'Mesh','off','XYGrid','on','ColorBar','off');
axis([-1 1 -1 1 umin umax]);
caxis([umin umax]);
xlabel x
ylabel y
zlabel u
M(i) = getframe;
end
-
函數
+關注
關注
3文章
4345瀏覽量
62867 -
生物學
+關注
關注
0文章
26瀏覽量
12991 -
數值模擬
+關注
關注
0文章
29瀏覽量
9605
發布評論請先 登錄
相關推薦




 關于MATLAB連續模型求解方法介紹和分析
關于MATLAB連續模型求解方法介紹和分析










評論