LQR算法是最優控制中經典的算法,而且LQR是一個應用較多的控制算法,所以在這里我以最優控制為起點介紹LQR控制算法。
注意LQR控制算法的基礎是你要有現代控制理論的基礎,需要知道狀態空間(State Space)。
1 最優控制問題實例分析
考慮一列火車 W,其質量為 m,沿著水平軌道運動,不考慮空氣的阻力和地面對火車的摩擦力,把火車看成一個沿著直線運動的質點,x(t)表示火車在t 時刻的位置,u(t)是施加在火車上的外部控制力,假設火車的初始位置和速度分別為 x(0)=x0,x' (0)=0要求選擇一個合適的外部控制函數 (t)使火車在最短時間內到達并靜止在坐標原點,即到達坐標原點時速度為零。
根據牛頓第二定律得火車的運動方程為
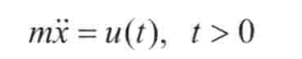
初始條件

終端條件

由于技術上的原因,外部推力不可能要多大就多大,它在數量上是有界的,即

其中,M是正常數

問題是尋找一個滿足式(1.1.4)的控制函數u(t),把W由初態(x0,0)'轉移到終態(0,0)',且使J(u)這個性能指標達到最小。任何能達到上述要求的控制函數都稱為最優控制。電梯的快速升降、軋鋼機的快速控制和機械振動的快速消振問題都可以用上述問題闡述。
2 最優控制的數學描述
由上述四個最優控制問題的實例可以看出,最優控制理論所要解決的問題是根據被控對象的動態特性(系統數學模型),選擇一個容許的控制律,使得被控對象按預定要求運行(由初始狀態運行到終端狀態),并使給定的某一性能指標達到最優值。因此,最優控制問題的數學描述應包含被控對象的數學模型、系統的邊界條件(初態和終態)、衡量“控制作用”效果的性能指標和容許控制四個方面的內容。
2.1 數學模型
被控對象的數學模型,即動態系統的微分方程,它反映了動態系統在運動過程中所應遵循的物理或化學規律,其運動規律可以用狀態方程來表示。
令x=(x1,…,xn)^T ∈ R^n 表示控制系統的狀態變量,u=(u1,…,um)^T ∈ R^m 表示控制系統的控制變量,則控制系統的狀態方程通常可用一階微分方程組描述為

方程式(1.2.1)概括了方程式(1.1.1)、式(1.1.6)和式(1.1.12)幾種情況.
當 f 不顯含 t 時,稱式(1.2.1)為 定常系統 (或稱為時不變系統)。當f關于x和u為線性關系時,稱式(1.2.1)為線性系統,這時方程可以寫成

其中,A(t)為n階方陣,B(t)為n 行 m 列矩陣。當A和B與時間t無關時,稱式(1.2.2)為線性定常系統或線性自治系統。
在一些實際問題中,系統的狀態變量和控制變量關于時間是離散的,這樣的控制系統稱為 離散控制系統 。令 x(k)=[x1(k),…,xn(k)]^T ∈ R^n 表示控制系統的狀態變量,u(k)=[u1(k),…,um(k)]^T ∈ R^m 表示控制系統的控制變量,則離散控制系統的狀態方程可用差分方程描述成

方程式(1.2.3)概括了方程式(1.1.15)的情況。
2.2 邊界條件
動態系統的初態和終態,也就是狀態方程的邊界條件 。動態系統的運動歸根結底是在狀態空間里從一個狀態轉移到另一個狀態,其運動隨時間變化對應于狀態空間的一條軌線。軌線的初始狀態可以記為 x(t0),n 為初始時間;軌線的終端狀態可記為 x(s),tf為達到終態的時間。
在最優控制問題中,當t=t0時的初態通常是已知的,即x(t0)=x,而到達終端的時間t和狀態x(tn)則因問題而異。就終端時間t來說,它可以有兩種情形:一種是固定的,如例1.3 中= 80 年,例 1.4 中= 3 年;另一種是變動或自由的,如例1.1 和例1.2。至于終端狀態 x(tn),情況要復雜得多,可歸納為以下三種情況:
** (1)終端狀態固定**
終端狀態固定指終端狀態x(tno)對應于狀態空間的一個固定點,即x(trsr是已知的如例1.1和例1.2中x(tf)=0,例13中x(tf)=0.5。
** (2)終端狀態受約束**
終端狀態受約束指終端狀態 x(tf) 受到一些條件的限制 ,如用以下方程表示 x(tf)必須滿足的約束條件。

** (3)終端狀態自由**
終端狀態自由指終端狀態x(sn)不再是一個點,而是一個運動點。
對于以上情況,都可以用一個目標集 S來概括,如果終端狀態固定,則目標集 S僅有一個元素;如果終端狀態受某些條件的約束,則目標集 S 為狀態空間的一個曲面;如果終端狀態自由,即不受任何條件的約束,則目標集 S 擴展到整個狀態空間。
2.3 性能指標
在狀態空間中從初始狀態轉移到終端狀態,可以通過不同的控制作用來實現,如何來衡量系統在控制作用下的好壞,需要用一個標準對它進行量化評定,這個評價的衡量尺度或標準我們稱之為性能指標。
值得著重指出的是:第一,我們無法為各種各樣的最優控制問題規定一個統一格式的性能指標,那種面面俱到的最優控制實際上是不存在的。第二,性能指標的內容和形式取決于最優控制問題所要解決的主要矛盾。第三,即使是同一個問題,其性能指標也可能因設計者著眼點的不同而異,如有的設計者注重縮短時間,有的設計者注重節省燃料,而有的設計者則兼顧縮短時間和節省燃料。因此,為了使性能指標規定得恰到好處,理論知識固不可少,但經驗和技巧的積累尤為重要。性能指標一般用J表示,在很多技術資料中被賦予不同的名稱,如性能泛函、價值函數、目標函數、效益函數等。
性能指標的數學表達主要有以下三種形式:
** (1)末值型性能指標,也稱為邁耶爾(Mayer)性能指標**

例1.1火車快速到達問題中,J(u)=tf-t0,即為末值型性能指標。
** (2)積分型性能指標,還稱為拉格朗日(Lagrange)性能指標**

例 1.3 基金的最優管理問題中,

即為積分型性能指標
** (3)復合型性能指標,也叫波爾扎(Bolza)性能指標**

復合型性能指標實際是末值型性能指標和積分型性能指標的組合,由式(1.2.7)可看出該指標對**控制過程的狀態量 x(t)、控制量 u(t)及末端狀態x(tf)**均有要求。
2.4 容許控制
對于一個實際的控制問題, 控制變量u(t)通常是某種物理量 。根據控制量的變化范圍,控制問題可分為兩類:一類是 控制量變化范圍受限制的控制 ,如控制船舶轉向的舵角、控制電機的電流都是受限制的;另一類是 控制量變化范圍不受限制或實際上不受限制的控制 ,如導彈的推力控制方向角,因可作+/-360°的變化而不受限制。
對每一個控制問題來說,滿足條件的控制作用u(t)的一個取值對應于m 維空間R^m中的一個點,所有滿足條件的控制作用 u(t)的取值構成 m 維空間的一個集合,記為,稱之為容許控制集。凡是屬于容許控制集 Ω 的控制都是容許控制。在前面提到的兩類控制中,前一類控制屬于閉集控制,后一類控制屬于開集控制。后續我們將會看到,這兩類控制問題,在處理方法上有著本質的區別。最優控制一定是容許控制,即

2.5 最優控制的一般提法
設已知系統的狀態方程為

初始條件和終端狀態滿足

控制函數為

其中,函數f是x(t)、u(t)和t的連續函數,并對x(t)和t連續可微。若存在一個在區間[t0,tf]中分段連續的控制函數u(t)能使系統狀態 x(t)從初態x0轉移到終態xf∈S,并使性能指標

達到極值,則稱控制函數 u(t)為最優控制函數,記為u* (t),與之對應的x(t)稱為最優軌線,記為x*(t),此時的性能指標J叫做最優性能指標。
可見,最優控制屬于系統綜合與設計范疇。最優控制的任務是給定一個被控系統(controlled system)或被控過程(controlled process)(包括有關的約束條件和邊界條件)以及性能指標(performance index),如何設計相應的控制系統(control system),使得在滿足約束條件和邊界條件的同時,其性能指標達到極值(極大或極小)。
2.6 離散系統最優控制問題的數學描述
設已知系統的差分方程為

初始條件和終端狀態滿足

控制函數為

性能指標

離散系統的最優控制問題就是尋求一個容許控制 u(k),使系統的狀態 x(k)從給定的初值0轉移到終態x(k) ∈S,并使性能指標J達到極值。
若上述最優控制問題有解u* (k),則u*(k)稱為最優控制函數,對應的軌x*(k)稱為最優軌線,而這時的性能指標J叫做最優性能指標
3 最優控制的發展
最優控制理論是現代控制理論的一個重要組成部分,它的發展與現代控制理論的發展是分不開的。迄今為止,控制理論的發展經歷了古典控制理論和現代控制理論的兩個重要發展階段,并進入了第三個階段,即大系統理論和 智能控制理論 。
第二次世界大戰以后發展起來的自動控制理論,在用來設計與分析單輸入單輸出的線性定常系統時是行之有效的。然而,隨著生產的發展,特別是空間技術的發展,控制系統日趨復雜,其精度要求愈來愈高。于是,建立在傳遞函數和頻率特性基礎上的自動控制理論,即我們通常說的經典控制理論,就日益顯示出它的局限性來。這種局限性首先表現在對于時變系統,傳遞函數根本無法定義;即使是線性定常系統,在多輸入多輸出時,其傳遞函數成為一個函數矩陣,以致從傳遞函數概念得出的工程上的結論,在這里也變得很復雜而難于應用。其次還表現在頻率法本質上是一種工程方法,由 頻率法所獲得的校正特性只能靠簡單的網絡來實現,而網絡參數的確定,還須經過調試過程,當系統很復雜,精度要求很高時,這種半經驗的方法就不大適用了 。因此,人們又回到時間域,建立了以狀態空間概念為基礎的現代控制理論。
現代控制理論所能處理的問題范圍很廣。原則上,它可以用來處理時變系統、非線性系統、多輸入多輸出系統以及分布參數系統的問題。用它來處理隨機系統問題和離散系統問題同樣是很方便的。
早在20世紀50年代初期,就有人發表了從工程觀點研究最短時間控制問題的文章,雖然最優性的證明借助于幾何圖形,帶有啟發性質,但它為現代控制理論的發展提供了第一批實際模型。隨后,最優控制問題的深入研究以及空間技術的迫切需要吸引了一大批數學家的密切注意。人們通過研究發現, 從數學觀點來看,最優控制問題就是求解一類帶有約束條件的泛函極值問題,其本質是一個變分學問題 。然而,經典變分理論所能解決的只是其容許控制屬于開集的一類最優控制問題,在工程實踐中所遇到的,卻大多是其容許控制屬于閉集的一類最優控制問題,經典變分理論無能為力,這就需要人們去探索求解最優控制問題的新途徑。
在種種新方法中,有兩種方法最富成效。一種是前蘇聯學者龐特里亞金(L.C.Pontryagin)的“極小值原理”:另一種是美國學者貝爾曼(RE.Bellman)的“動態規劃”。
受力學中哈密爾頓原理的啟發,龐特里亞金等人把“極小值原理”作為一種推測首先提出來,隨后不久又提供了一種嚴格的證明,并于1958年在愛丁堡召開的國際數學會議上首次宣讀。“極小值原理”發展了經典變分原理,成為處理閉集性約束變分問題的強有力工具。
“動態規則”是貝爾曼在1953至1957年間逐步創立的,他依據最優性原理,發展了變分學中的哈密爾頓-雅可比(Hamilton-Jacobi) 理論,構成了“動態規劃”,它是一種適用于計算機計算、處理問題范圍更廣泛的方法。在現代控制理論的形成與發展中,極小值原理、動態規劃和卡爾曼的最優估計理論起了重要的推動作用。現代控制理論迅速發展的同時,數字計算機也在飛速地發展,并得到廣泛地應用。數字計算機運算速度的提高、存儲容量的增大、體積的縮小以及軟件的廣泛應用,使數字計算機不僅成為控制系統分析與設計的強有力的工具,而且逐漸成為自動控制系統的主要部件之一。計算機“在線”參與控制,使得許多既不要求把控制器歸結為簡單的校正網絡,也不要求有封閉式解析解的復雜控制方法在實際工程應用中成為可能。因此,高速度、大容量、軟硬結合計算機的問世,一方面使現代控制理論的工程實現有了可能,另一方面又反過來提出許多新的理論和問題,導致諸如最優控制的直接和間接計算的大批研究成果的出現,進一步推動了現代控制理論的發展。
近20年來,在現代控制理論和現代控制工程應用中, 吸收了現代數學的很多成果 ,又得到了很大發展,并滲透到生產、生活、國防、城市規劃、智能交通、管理等許多領域.發揮了愈來愈大的作用。最優控制的發展成果主要包括分布式參數的最優控制、隨機最優控制、自適應控制、大系統最優控制、微分對策等,最優控制理論形成了比較完善的理論體系,為現代控制工程做了比較充分的理論準備。特別要指出的是,隨著高性能嵌入式系統的應用和發展,最優控制理論研究將是一個十分活躍的研究領域,最優控制理論在實際工程中應用將愈來愈廣泛。
-
控制算法
+關注
關注
4文章
166瀏覽量
21761 -
現代控制
+關注
關注
0文章
5瀏覽量
1298 -
LQR
+關注
關注
1文章
6瀏覽量
3158
發布評論請先 登錄
相關推薦
主動隊列管理建模及最優控制策略
基于LQR 的直升機最優控制系統的設計Design on a
大純滯后對象的最優控制
狀態時滯系統的輸入多采樣最優控制
基于LQR最優調節器的倒立擺控制系統
一種多諧振最優伺服控制算法在中頻電源設計中應用
什么是機器人最優控制和逆最優控制
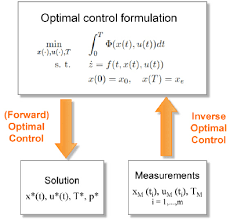




 LQR控制算法之最優控制
LQR控制算法之最優控制











評論