各個環節的特點:
比例作用:輸出與輸入曲線相似;
積分作用:只要輸入有偏差輸出就變化;
微分作用:輸入有抖動輸出才有變化,且會猛烈變化。
01對微分的理解
系統的輸出量與輸入量對時間的微分成正比,即輸出量反映輸入量的變化率,而不反映輸入量本身的大小。因此,可由微分環節的輸出來反映輸入信號的變化趨勢,加快系統控制作用實現。所以常用微分環節來改善系統的動態響應。
微分的作用能夠超前調節,單純的微分作用是不存在的,同積分作用一樣。
1.微分作用與被調量的大小無關,但與被調量的變化速率有關;
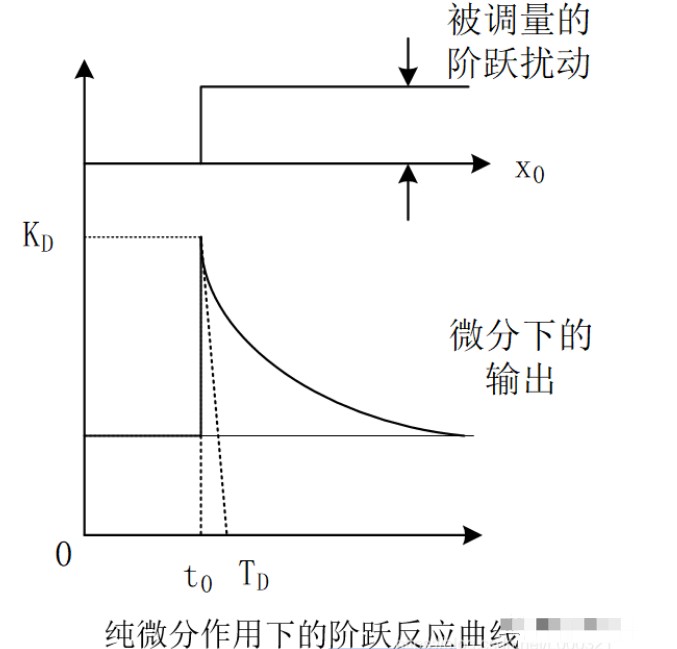
2.微分參數一般只有一個,用微分時間表示。有些有兩個:微分增益與微分時間。但是我們一般只調節微分增益。微分增益表示輸出波動的幅度,波動后還要輸出回歸,微分時間表示回歸的快慢。從下圖可以稍微理解一下:
02微分適用范圍
對于微分項的適用,不是所有的系統都適用。很多人常常會將比例積分微分一起用于系統的控制。比例積分可以都適用,但是有些系統用微分是不恰當的。
1.被調量很難穩定在一個數值,微分作用會因為被調量的小波動,使得輸出大幅度來回動作,形成干擾,而且對執行機構也不利。就如被調量是水位、氣壓、風壓的調節系統不適合使用微分。他們本身的數值容易受各種因素影響,即使穩定的系統,被調量也很難穩定在一個數值。就如我現在研究生學習階段的方向是永磁同步電機的控制,在采用PID控制時,一般不引入微分控制;
2.被調量有微小擾動時,要先消除擾動再使用微分;
3.系統大延遲的情況下應使用微分。
03仿真實驗分析
搭建PID控制器如圖所示,為保證仿真的有效性,仿真的控制對象與采用Pi控制的參數與對象均為一階慣性函數。微分增益一般取很小的值,初步取值為0.1。
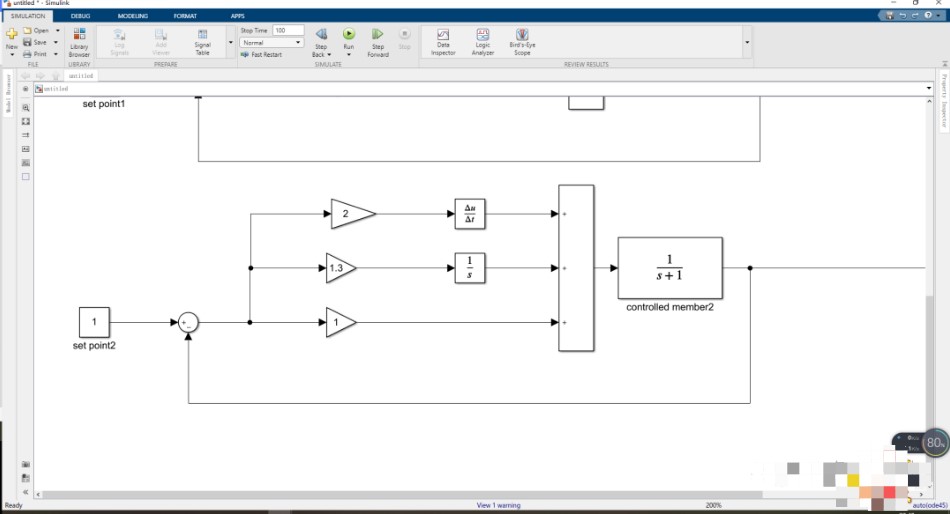
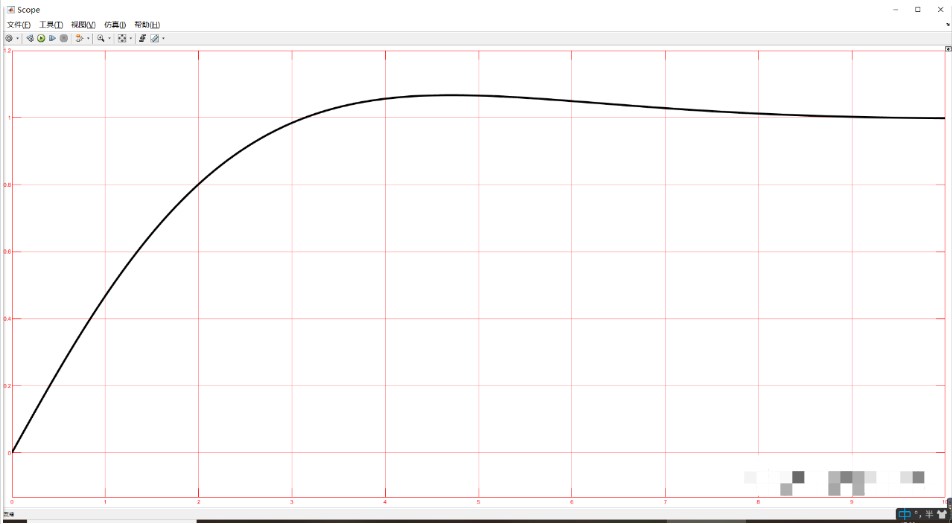
可以從仿真看出,輸出逐步趨于期望值最后并穩定于1。閉環傳遞函數為:
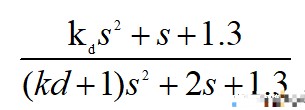
化為一般式:
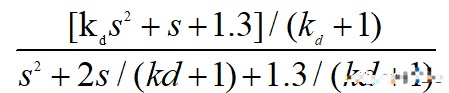
當s趨于0,即時間趨于無窮大時,其輸出為1。
(從時域分析)要讓系統響應無震蕩和超調,那就要讓系統處于一個臨界阻尼狀態。欠阻尼狀態理解為系統的最佳狀態,即ε要在[0,1]之間取值,二階系統在欠阻尼時的響應為衰減震蕩的,所以必然存在超調。從書本上了解到對于一個二階系統在單位階躍輸入信號作用下的傳遞函數為:
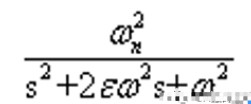
對于當前的仿真系統而言,其ki的計算值應該小于零。但是參數一般不可以是負數。大回路已經有負反饋了,再有負參數,成正反饋了,系統會不穩定。這個時候自己的理解就是不到萬不得以,盡量不使用微分項,實在是太難調了。
04總結
1.微分項不到萬不得已還是不要用了,頭痛!微分項不適用任何系統,要根據系統的特性來使用,不然會適得其反;
2. 微分作用:輸入有抖動輸出才有變化,且會猛烈變化。微分就是提前預測控制;
3.當系統出現震蕩時,可能不單單只與某一項參數有關,一定要仔細判斷震蕩曲線的特性,分辨出是哪個因素造成的,然后對癥下藥才能抑制震蕩。
-
控制器
+關注
關注
112文章
16376瀏覽量
178194 -
PID
+關注
關注
35文章
1472瀏覽量
85544 -
曲線
+關注
關注
1文章
82瀏覽量
20862 -
控制算法
+關注
關注
4文章
166瀏覽量
21728 -
微分
+關注
關注
0文章
31瀏覽量
14109
發布評論請先 登錄
相關推薦




 PID控制算法詳解(三)
PID控制算法詳解(三)













評論