本文旨在為沒有接觸過形式化方法的讀者提供一種新的視角看待計算機系統與算法,而非形式化方法或 TLA+ 教程。因此本文的重點是如何從數學角度思考程序,不會使用大篇幅講解 TLA+ 的語法。
1
我們該如何寫出正確的程序?
程序設計的目標永遠是寫出正確的程序。隨著時間的推移,我們的程序越來越復雜,其中可能存在的錯誤也越來越多。想要寫出正確的程序,首先應該了解程序中可能出現的錯誤有哪些。
程序中會有什么樣錯誤?
我將程序中可能出現的錯誤粗略地分為兩類:簡單錯誤與邏輯錯誤。
簡單錯誤
簡單錯誤包含語義錯誤、內存錯誤等。對于這些容易分析的簡單錯誤,我們已經有很多成熟的方法與工具來避免,如編譯器、靜態分析工具、Garbage Collector 等。由于這類錯誤可以比較容易地被發現與修復,因此不是我們關注的重點。
邏輯錯誤
邏輯錯誤是程序中最難發現的錯誤,也是最難修復的錯誤,如死鎖、競態條件、數據不一致等。邏輯錯誤影響了程序的正確性、性能、可靠性等指標,通常是由于程序的設計不夠完善導致的。對于這類錯誤,我們需要從更高的層面來分析與設計程序,而非僅僅從代碼的實現細節來考慮。
我們通常會使用一些方法來避免邏輯錯誤,如:
- 優化軟件架構設計- 在設計階段就考慮程序的正確性,避免設計出不夠完善的程序
- 測試- 使用各種測試方法來減少程序的錯誤,但無法保證程序的完全正確
越有經驗的人往往能想到更多的細節與可能性,設計出的系統通常更穩定。但我們不能僅僅依賴于經驗:
- 經驗有局限性- 人類的經驗是有限且不可靠的
- 復雜系統的行為、狀態太多- 一個復雜的系統,其行為與狀態太多,很難通過經驗來預測
- 特定程序對正確性的要求很高- 有些程序對正確性的要求很高,如金融系統、醫療系統等,這些程序的正確性很難通過經驗來保證
- 無法從理論上驗證正確性- 只能盡量減少錯誤的發生,但無法從理論上證明程序的正確性
綜上,我們需要一種更加嚴謹的方法,從設計上保證程序的正確性。
形式化方法如果能夠從數學角度驗證一個程序的正確性,就可以解決上述的問題,這就是形式化方法的目標。
形式化方法基于數學,通過為系統建立數學模型,來定義系統的行為、狀態等,然后定義系統的約束條件,如安全性、活性,最終證明模型滿足系統形式規約,來驗證系統的正確性。對于有窮狀態的系統,可以使用以窮盡搜索為基礎的模型檢測,通過搜索待驗證系統模型的有窮狀態空間來檢驗該系統的行為是否具備預期屬性。對于有無窮狀態空間的系統,使用邏輯推理為基礎的演繹驗證,利用歸納法驗證系統的正確性。
本文用 TLA+ 語言作為工具來介紹形式化方法。
2
TLA+
TLA+ 的作者是在并發和分布式系統領域做出開創性貢獻的 2013 年圖靈獎獲得者,計算機科學家 Leslie Lamport。
TLA+ 是一種用于對程序和系統進行建模的高級語言——尤其是并發和分布式程序和系統。其核心思想是:精確描述事物的最佳方式是使用簡單的數學。TLA+ 及其工具可用于消除的設計錯誤,這些錯誤很難在代碼中發現并且糾正起來代價高昂。
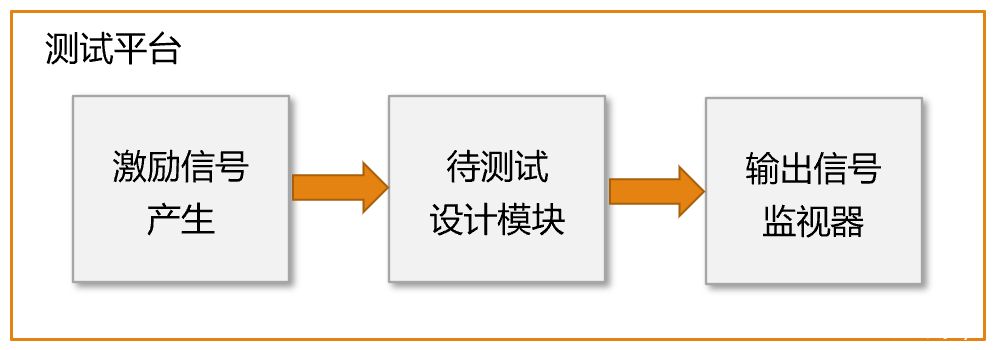
使用 TLA+ 編寫的 specification 并不是真正的工程代碼,無法用在生產環境中,因為 TLA+ 的目標是在系統設計階段就發現并解決邏輯錯誤。在 TLA+ 中,我們將程序抽象為有窮狀態的數學模型,通常是狀態機,然后利用 TLC Model Checker 窮盡程序所有可能到達的狀態并驗證其正確性。
下面通過兩個簡單的例子介紹 TLA+。這兩個例子均來自 TLA+ 作者的 Leslie Lamport's The TLA+ Video Course。本文的目標是為沒有接觸過形式化方法的讀者提供一種新的視角看待計算機系統與算法,而不是 TLA+ 教程,因此不會過多介紹 TLA+ 的語法與工具的使用。
簡單的例子TLA+ 可以讓我們使用簡單的數學抽象系統模型,主要是集合論與布爾邏輯。在抽象的過程中,我們要舍棄很多實現細節,僅關注程序的邏輯本身。
下面是一個簡單的 C 語言程序,我們嘗試將其抽象為一個 TLA+ 程序:
inti;
voidmain(){
i=someNumber();//someNumber()用來得到一個0到1000之間的數字
i=i+1;
}
狀態抽象
我們需要將這個程序抽象為一個個獨立的狀態。很顯然,對于這個簡單的程序,各狀態之間的不同點只有i的值。假設i在初始化后的默認值是 0,且某次運行這個程序時someNumber()返回了 42,那么這個程序存在的狀態轉換關系就是:
[i : 0] -> [i : 42] -> [i : 43]
這之中有三個狀態,每個狀態間的區別均為i的值不同。
這樣看似完成了抽象,但是這個抽象還是有問題的。假設在另一次運行中,someNumber()返回了 43,那么這個程序的狀態轉換關系就是:
[i : 0] -> [i : 43] -> [i : 44]
這與之前的抽象不符,因為兩次運行的狀態轉換關系不同。這是因為我們沒有考慮到someNumber()的返回值。
程序的"狀態"是指程序運行完成各個階段后的時間點,而不是程序運行的過程。因此,每個狀態都是獨立的,且狀態之間的轉換都是原子的。這與傳統的編程有很大的區別,因為傳統的編程是面向過程的,而 TLA+ 是面向狀態的。我們只在乎目前程序運行到了什么狀態,因此可以引入一個變量pc來表示程序運行到了哪個階段,這樣我們就可以清晰地表示程序的次態關系:
inti;
voidmain(){
i=someNumber();//pc="start"
i=i+1;//pc="middle"
}//pc="done"
這樣,我們不需要再考慮i的值,只需要考慮pc的值即可:[pc : start] -> [pc : middle] -> [pc : done]
狀態編寫
i的初始值為 0,pc的初始值為start,我們可以把次態關系寫成:

其中,對于變量i,它的下一個狀態表示為i',這是 TLA+ 中定義變量狀態轉換的方式。i' ∈ 0..1000代表i在下一個狀態的值是 0 到 1000 之間的一個數,也就是someNumber(),0..1000代表集合{0,1,...,1000}。∧是布爾邏輯中的邏輯與,可以認為意為"并且"。最終程序運行完成,不會再有下一個狀態,因此表示為FALSE。
在 TLA+ 中,我們編寫的是一個個狀態。因此,并非是"因為pc = start所以i' ∈ 0..1000",事實上兩者的關系是并列的:**在這個狀態中,pc的值是start并且i下一個狀態的值∈ 0..1000**。有了這樣的思想,我們可以將上面的抽象改寫為:

∨來表示。這樣,我們就可以清晰地表示出程序的狀態轉換關系了。為了美觀,在 TLA+ 中,首句前也可以補上相同的布爾邏輯符號:
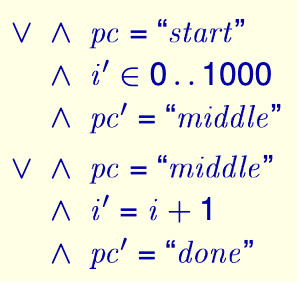

-
EXTENDS用于引入其他 specification 中定義的 module,這里引入了標準庫中的Integers,主要用在i' ∈ 0..1000上。 -
VARIABLES用于定義變量,這里定義了i和pc。 -
Init用于定義初始狀態,這里定義了i = 0和pc = "start"。 -
Next用于定義狀態轉換關系。
二階段提交(英語:Two-phase Commit)是指在計算機網絡以及數據庫領域內,為了使基于分布式系統架構下的所有節點在進行事務提交時保持一致性而設計的一種算法。通常,二階段提交也被稱為是一種協議(Protocol)。在分布式系統中,每個節點雖然可以知曉自己的操作時成功或者失敗,卻無法知道其他節點的操作的成功或失敗。當一個事務跨越多個節點時,為了保持事務的ACID特性,需要引入一個作為協調者的組件來統一掌控所有節點(稱作參與者)的操作結果并最終指示這些節點是否要把操作結果進行真正的提交(比如將更新后的數據寫入磁盤等等)。因此,二階段提交的算法思路可以概括為:參與者將操作成敗通知協調者,再由協調者根據所有參與者的反饋情報決定各參與者是否要提交操作還是中止操作。——Two-Phase Commit (Wikipedia)
在Leslie Lamport's The TLA+ Video Course中,Lamport 以這樣的方式類比解釋 Two-Phase Commit:
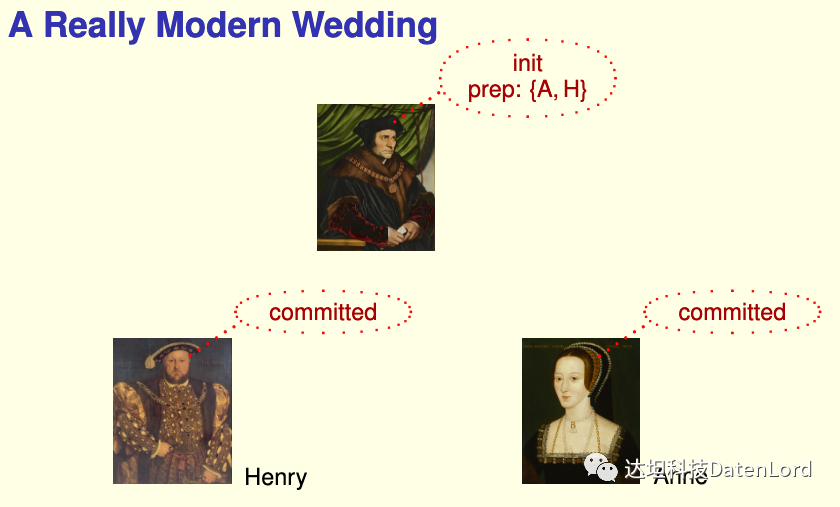
在婚禮上,牧師是協調者,新郎和新娘是參與者。當新郎和新娘都同意婚事時,牧師才會正式宣布婚事。如果有一方不同意,牧師就會中止婚事:
- 牧師問新郎:你是否同意這件婚事?
- 新郎回答:我同意(prepared)。
- 牧師問新娘:你是否同意這件婚事?
- 新娘回答:我同意(prepared)。
- 牧師宣布:婚事正式成立(committed)。
如果其中有一方不同意,牧師就會中止(abort)婚事。
在數據庫中,Transaction Manager 是協調者(牧師)。當 Transaction Manager 詢問所有參與者 Resource Managers (新郎 / 新娘)時,如果所有 Resource Managers 都同意提交事務,Transaction Manager 就會把事務提交。如果有一方不同意,Transaction Manager 就會中止事務。
Two-Phase Commit 的詳細介紹與流程可以在Wikipedia上找到。
首先我們來定義一些常量與變量以及其初始狀態:

-
常量
RM是所有 Resource Manager 標識的集合,例如可以設為集合{"r1", "r2", "r3"}。 -
變量
rmState用于記錄每個 Resource Manager 的狀態,用rmState[r]表示r的狀態,有working、prepared、committed、aborted四種狀態,每個RM的初始狀態均為working。 -
變量
tmState用于記錄 Transaction Manager 的狀態,有init、committed、aborted三種狀態,初始狀態為init。 -
變量
tmPrepared用于記錄已經準備好(處于prepared狀態)的 Resource Manager,初始值是一個空集。 -
變量
msgs作為消息池,用于記錄所有正在傳輸的消息,初始值是一個空集。
下面我們來定義系統做可能發生的動作。

- TLA+ 中可以用上述方式定義類似于其它編程語言中"函數"概念的表達式,這樣就無需對每一個 Resource Manager 都定義一個表達式了。
-
[type → "prepare", rm → r]是一個 TLA+ 中的 record,類似于其它編程語言中的 struct。 -
UNCHANGED ?rmState, tmState, msgs?表示這個動作不會改變rmState、tmState、msgs這三個變量的值。在 TLA+ 中,每一個變量的值是否改變都需要顯式地聲明。
當TM的狀態為init,且在消息池中存在來自r的Prepared消息,tmPrepared在下一個狀態的值會是tmPrepared和{r}的并集。
 上面的兩個動作分別是 Transaction Manager 進行 Commit 與 Abort。
上面的兩個動作分別是 Transaction Manager 進行 Commit 與 Abort。

上述 4 個 Resource Manager 動作分別是 Resource Manager 選擇 Prepare 與 Abort,以及處理由 Transaction Manager 決定的 Commit 與 Abort。
其中,存在語法如rmState' = [rmState except ![r] = "prepared"],意為"在下一個狀態中,rmState[r]的值變為prepared,其它部分不變"。
如果我們用形如rmState[r]' = "prepared"的形式來表示,我們并沒有顯式地說明rmState的其它部分在下一個狀態的值,因此是不正確的。
TLA+ 與我們通常編寫的程序不同,是數學。在編程中,我們會使用到數組,而在 TLA+ 中,我們使用函數來表達類似的概念,數組的下標組成的集合就是函數的定義域。
編寫完系統可能存在的所有動作后,我們就可以開始歸納系統的狀態轉換了:

其中,我們使用存在量詞?r ∈ RM來表示"對于集合RM的任意元素r,都存在這種行為"。TLA+ 的狀態轉換是原子的,因此在一個狀態中這個"或"分支內只會有一個r被選擇,這可以類比為編程語言中的for r in RM,但在本質上不同。
至此,對系統的建模就完成了。下面我們需要編寫系統的約束條件:

TypeOK中,我們將每個變量的可能值都進行了限制。其中的[RM → {"working","prepared", "committed", "aborted"}]是類似于將集合RM與集合{"working", "prepared", "committed", "aborted"}做笛卡爾積的操作,但得到的是一個由 record 組成的集合:
{
[r1|->"working",r2|->"working"],
[r1|->"working",r2|->"prepared"],
[r1|->"working",r2|->"committed"],
...
[r1|->"aborted",r2|->"committed"],
[r1|->"aborted",r2|->"aborted"]
}
在TypeOK中我們用到了上面定義的集合Messages。定義Messages時,我們使用了語法:[type: {"Prepared"}, rm: RM]。這種語法也是對{"Prepared"}與RM做類似笛卡爾積的操作,但得到的也是一個 record 集合:
{
[type|->"Prepared",rm|->r1],
[type|->"Prepared",rm|->r2],
...
}最
最后的約束條件Consistent用于保證系統的一致性:在任意時刻,系統中不可能存在兩個 Resource Managers 分別處于committed和abort狀態。
最終,我們將約束條件作為不變量,與系統模型一起交給 TLC Model Checker 進行驗證,就可以證明系統的正確性。
3
總結
通過上面的兩個例子,我們初步了解形式化方法的思想。TLA+ 是為了驗證分布式系統而設計的,但其思想可以應用到的領域遠不止分布式系統。在編寫程序時,如果我們能夠不僅僅考慮代碼層面的內容,而是從更高的層面,從數學角度去思考,就能夠寫出更加健壯的程序。如果你對 TLA+ 感興趣,可以參考Leslie Lamport's The TLA+ Video Course - YouTube與Learn TLA+。4
我們的項目:Xline
TLA+被廣泛用于分布式系統算法的研究和開發中。在我們的項目Xline中,TLA+被用來在設計階段驗證共識算法的正確性。
Xline是一個用于元數據管理的分布式KV存儲。我們在Xline中使用CURP協議(https://www.usenix.org/system/files/nsdi19-park.pdf)的修改版作為共識協議,TLA+將被用于其正確性驗證中。
如果你想了解更多關于Xline的信息,請參考我們的Github:https://github.com/datenlord/Xline
審核編輯 :李倩
-
算法
+關注
關注
23文章
4628瀏覽量
93186 -
程序
+關注
關注
117文章
3795瀏覽量
81289 -
架構設計
+關注
關注
0文章
32瀏覽量
6968
原文標題:從數學角度思考程序與驗證正確性
文章出處:【微信號:Rust語言中文社區,微信公眾號:Rust語言中文社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一種新型半自動驗證流程 SoC連通性的正確性
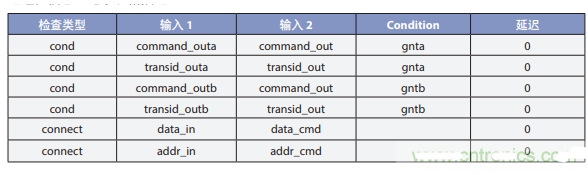
ADS5282如何通過其他方式驗證寄存器寫入的正確性?
驗證了LCL型濾波器參數設計及光伏并入配電網的逆變器電壓控制策略的正確性

如何驗證區塊鏈開發程序和驗證程序的正確性
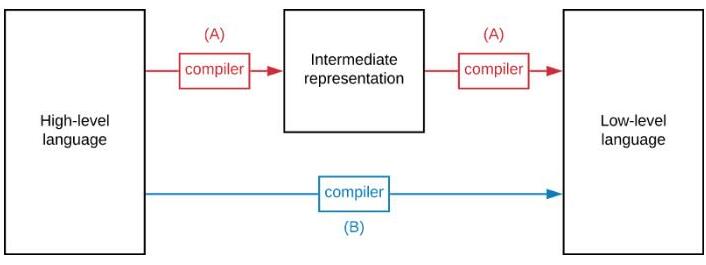




 從數學角度思考程序與驗證正確性
從數學角度思考程序與驗證正確性











評論