1.1.4 加權(quán)分位數(shù)縮略圖

事實(shí)上， XGBoost 不是簡(jiǎn)單地按照樣本個(gè)數(shù)進(jìn)行分位，而是以二階導(dǎo)數(shù)值 作為樣本的權(quán)重進(jìn)行劃分，如下：

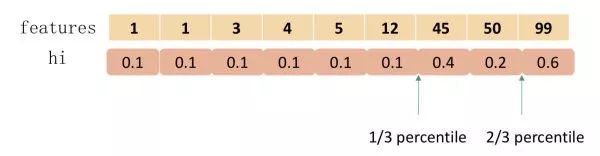
那么問(wèn)題來(lái)了：為什么要用 進(jìn)行樣本加權(quán)？

我們知道模型的目標(biāo)函數(shù)為：

我們稍作整理，便可以看出 有對(duì) loss 加權(quán)的作用。

其中 與 C 皆為常數(shù)。我們可以看到 h_i 就是平方損失函數(shù)中樣本的權(quán)重。

對(duì)于樣本權(quán)值相同的數(shù)據(jù)集來(lái)說(shuō)，找到候選分位點(diǎn)已經(jīng)有了解決方案（GK 算法），但是當(dāng)樣本權(quán)值不一樣時(shí)，該如何找到候選分位點(diǎn)呢？（作者給出了一個(gè) Weighted Quantile Sketch 算法，這里將不做介紹。）

1.1.5 稀疏感知算法

在決策樹(shù)的第一篇文章中我們介紹 CART 樹(shù)在應(yīng)對(duì)數(shù)據(jù)缺失時(shí)的分裂策略，XGBoost 也給出了其解決方案。

XGBoost 在構(gòu)建樹(shù)的節(jié)點(diǎn)過(guò)程中只考慮非缺失值的數(shù)據(jù)遍歷，而為每個(gè)節(jié)點(diǎn)增加了一個(gè)缺省方向，當(dāng)樣本相應(yīng)的特征值缺失時(shí)，可以被歸類到缺省方向上，最優(yōu)的缺省方向可以從數(shù)據(jù)中學(xué)到。至于如何學(xué)到缺省值的分支，其實(shí)很簡(jiǎn)單，分別枚舉特征缺省的樣本歸為左右分支后的增益，選擇增益最大的枚舉項(xiàng)即為最優(yōu)缺省方向。

在構(gòu)建樹(shù)的過(guò)程中需要枚舉特征缺失的樣本，乍一看該算法的計(jì)算量增加了一倍，但其實(shí)該算法在構(gòu)建樹(shù)的過(guò)程中只考慮了特征未缺失的樣本遍歷，而特征值缺失的樣本無(wú)需遍歷只需直接分配到左右節(jié)點(diǎn)，故算法所需遍歷的樣本量減少，下圖可以看到稀疏感知算法比 basic 算法速度塊了超過(guò) 50 倍。

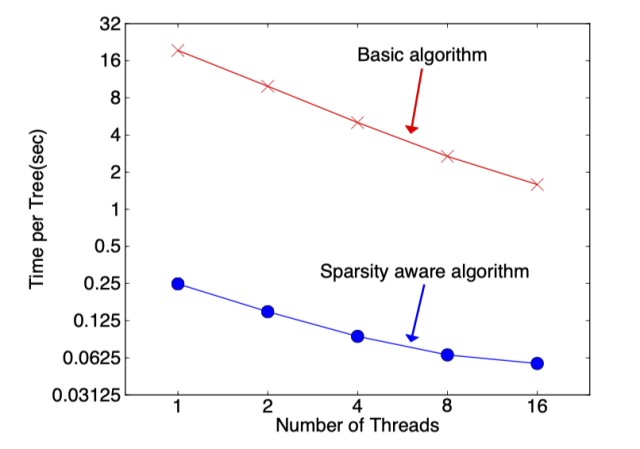
1.2 工程實(shí)現(xiàn)

1.2.1 塊結(jié)構(gòu)設(shè)計(jì)

我們知道，決策樹(shù)的學(xué)習(xí)最耗時(shí)的一個(gè)步驟就是在每次尋找最佳分裂點(diǎn)是都需要對(duì)特征的值進(jìn)行排序。而 XGBoost 在訓(xùn)練之前對(duì)根據(jù)特征對(duì)數(shù)據(jù)進(jìn)行了排序，然后保存到塊結(jié)構(gòu)中，并在每個(gè)塊結(jié)構(gòu)中都采用了稀疏矩陣存儲(chǔ)格式（Compressed Sparse Columns Format，CSC）進(jìn)行存儲(chǔ)，后面的訓(xùn)練過(guò)程中會(huì)重復(fù)地使用塊結(jié)構(gòu)，可以大大減小計(jì)算量。

• 每一個(gè)塊結(jié)構(gòu)包括一個(gè)或多個(gè)已經(jīng)排序好的特征；
• 缺失特征值將不進(jìn)行排序；
• 每個(gè)特征會(huì)存儲(chǔ)指向樣本梯度統(tǒng)計(jì)值的索引，方便計(jì)算一階導(dǎo)和二階導(dǎo)數(shù)值；

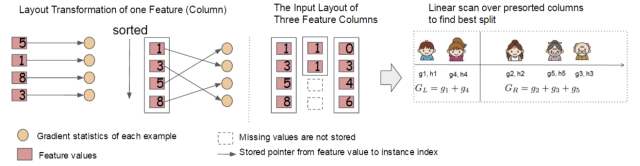
這種塊結(jié)構(gòu)存儲(chǔ)的特征之間相互獨(dú)立，方便計(jì)算機(jī)進(jìn)行并行計(jì)算。在對(duì)節(jié)點(diǎn)進(jìn)行分裂時(shí)需要選擇增益最大的特征作為分裂，這時(shí)各個(gè)特征的增益計(jì)算可以同時(shí)進(jìn)行，這也是 Xgboost 能夠?qū)崿F(xiàn)分布式或者多線程計(jì)算的原因。

1.2.2 緩存訪問(wèn)優(yōu)化算法

塊結(jié)構(gòu)的設(shè)計(jì)可以減少節(jié)點(diǎn)分裂時(shí)的計(jì)算量，但特征值通過(guò)索引訪問(wèn)樣本梯度統(tǒng)計(jì)值的設(shè)計(jì)會(huì)導(dǎo)致訪問(wèn)操作的內(nèi)存空間不連續(xù)，這樣會(huì)造成緩存命中率低，從而影響到算法的效率。

為了解決緩存命中率低的問(wèn)題，XGBoost 提出了緩存訪問(wèn)優(yōu)化算法：為每個(gè)線程分配一個(gè)連續(xù)的緩存區(qū)，將需要的梯度信息存放在緩沖區(qū)中，這樣就是實(shí)現(xiàn)了非連續(xù)空間到連續(xù)空間的轉(zhuǎn)換，提高了算法效率。

此外適當(dāng)調(diào)整塊大小，也可以有助于緩存優(yōu)化。

1.2.3 “核外”塊計(jì)算

當(dāng)數(shù)據(jù)量過(guò)大時(shí)無(wú)法將數(shù)據(jù)全部加載到內(nèi)存中，只能先將無(wú)法加載到內(nèi)存中的數(shù)據(jù)暫存到硬盤中，直到需要時(shí)再進(jìn)行加載計(jì)算，而這種操作必然涉及到因內(nèi)存與硬盤速度不同而造成的資源浪費(fèi)和性能瓶頸。為了解決這個(gè)問(wèn)題，XGBoost 獨(dú)立一個(gè)線程專門用于從硬盤讀入數(shù)據(jù)，以實(shí)現(xiàn)處理數(shù)據(jù)和讀入數(shù)據(jù)同時(shí)進(jìn)行。

此外，XGBoost 還用了兩種方法來(lái)降低硬盤讀寫的開(kāi)銷：

• 塊壓縮：對(duì) Block 進(jìn)行按列壓縮，并在讀取時(shí)進(jìn)行解壓；
• 塊拆分：將每個(gè)塊存儲(chǔ)到不同的磁盤中，從多個(gè)磁盤讀取可以增加吞吐量。

1.3 優(yōu)缺點(diǎn)

1.3.1 優(yōu)點(diǎn)

1. 精度更高：GBDT 只用到一階泰勒展開(kāi)，而 XGBoost 對(duì)損失函數(shù)進(jìn)行了二階泰勒展開(kāi)。XGBoost 引入二階導(dǎo)一方面是為了增加精度，另一方面也是為了能夠自定義損失函數(shù)，二階泰勒展開(kāi)可以近似大量損失函數(shù)；
2. 靈活性更強(qiáng)：GBDT 以 CART 作為基分類器，XGBoost 不僅支持 CART 還支持線性分類器，（使用線性分類器的 XGBoost 相當(dāng)于帶 L1 和 L2 正則化項(xiàng)的邏輯斯蒂回歸（分類問(wèn)題）或者線性回歸（回歸問(wèn)題））。此外，XGBoost 工具支持自定義損失函數(shù)，只需函數(shù)支持一階和二階求導(dǎo)；
3. 正則化：XGBoost 在目標(biāo)函數(shù)中加入了正則項(xiàng)，用于控制模型的復(fù)雜度。正則項(xiàng)里包含了樹(shù)的葉子節(jié)點(diǎn)個(gè)數(shù)、葉子節(jié)點(diǎn)權(quán)重的 L2 范式。正則項(xiàng)降低了模型的方差，使學(xué)習(xí)出來(lái)的模型更加簡(jiǎn)單，有助于防止過(guò)擬合；
4. Shrinkage（縮減）：相當(dāng)于學(xué)習(xí)速率。XGBoost 在進(jìn)行完一次迭代后，會(huì)將葉子節(jié)點(diǎn)的權(quán)重乘上該系數(shù)，主要是為了削弱每棵樹(shù)的影響，讓后面有更大的學(xué)習(xí)空間；
5. 列抽樣：XGBoost 借鑒了隨機(jī)森林的做法，支持列抽樣，不僅能降低過(guò)擬合，還能減少計(jì)算；
6. 缺失值處理：XGBoost 采用的稀疏感知算法極大的加快了節(jié)點(diǎn)分裂的速度；
7. 可以并行化操作：塊結(jié)構(gòu)可以很好的支持并行計(jì)算。

1.3.2 缺點(diǎn)

1. 雖然利用預(yù)排序和近似算法可以降低尋找最佳分裂點(diǎn)的計(jì)算量，但在節(jié)點(diǎn)分裂過(guò)程中仍需要遍歷數(shù)據(jù)集；
2. 預(yù)排序過(guò)程的空間復(fù)雜度過(guò)高，不僅需要存儲(chǔ)特征值，還需要存儲(chǔ)特征對(duì)應(yīng)樣本的梯度統(tǒng)計(jì)值的索引，相當(dāng)于消耗了兩倍的內(nèi)存。

LightGBM

LightGBM 由微軟提出，主要用于解決 GDBT 在海量數(shù)據(jù)中遇到的問(wèn)題，以便其可以更好更快地用于工業(yè)實(shí)踐中。

從 LightGBM 名字我們可以看出其是輕量級(jí)（Light）的梯度提升機(jī)（GBM），其相對(duì) XGBoost 具有訓(xùn)練速度快、內(nèi)存占用低的特點(diǎn)。下圖分別顯示了 XGBoost、XGBoost_hist（利用梯度直方圖的 XGBoost） 和 LightGBM 三者之間針對(duì)不同數(shù)據(jù)集情況下的內(nèi)存和訓(xùn)練時(shí)間的對(duì)比：

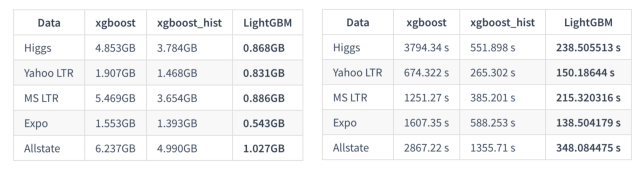
那么 LightGBM 到底如何做到更快的訓(xùn)練速度和更低的內(nèi)存使用的呢？

我們剛剛分析了 XGBoost 的缺點(diǎn)，LightGBM 為了解決這些問(wèn)題提出了以下幾點(diǎn)解決方案：

1. 單邊梯度抽樣算法；
2. 直方圖算法；
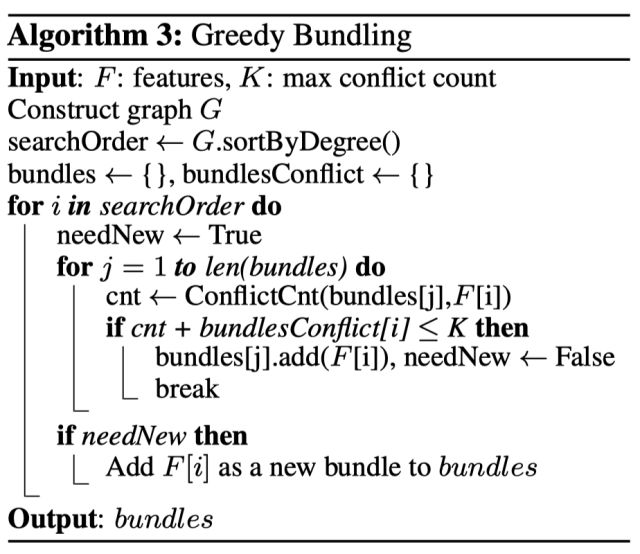
3. 互斥特征捆綁算法；
4. 基于最大深度的 Leaf-wise 的垂直生長(zhǎng)算法；
5. 類別特征最優(yōu)分割；
6. 特征并行和數(shù)據(jù)并行；
7. 緩存優(yōu)化。

本節(jié)將繼續(xù)從數(shù)學(xué)原理和工程實(shí)現(xiàn)兩個(gè)角度介紹 LightGBM。

2.1 數(shù)學(xué)原理

2.1.1 單邊梯度抽樣算法

GBDT 算法的梯度大小可以反應(yīng)樣本的權(quán)重，梯度越小說(shuō)明模型擬合的越好，單邊梯度抽樣算法（Gradient-based One-Side Sampling, GOSS）利用這一信息對(duì)樣本進(jìn)行抽樣，減少了大量梯度小的樣本，在接下來(lái)的計(jì)算鍋中只需關(guān)注梯度高的樣本，極大的減少了計(jì)算量。

GOSS 算法保留了梯度大的樣本，并對(duì)梯度小的樣本進(jìn)行隨機(jī)抽樣，為了不改變樣本的數(shù)據(jù)分布，在計(jì)算增益時(shí)為梯度小的樣本引入一個(gè)常數(shù)進(jìn)行平衡。具體算法如下所示：

我們可以看到 GOSS 事先基于梯度的絕對(duì)值對(duì)樣本進(jìn)行排序（無(wú)需保存排序后結(jié)果），然后拿到前 a% 的梯度大的樣本，和剩下樣本的 b%，在計(jì)算增益時(shí)，通過(guò)乘上 \\frac{1-a}{b} 來(lái)放大梯度小的樣本的權(quán)重。一方面算法將更多的注意力放在訓(xùn)練不足的樣本上，另一方面通過(guò)乘上權(quán)重來(lái)防止采樣對(duì)原始數(shù)據(jù)分布造成太大的影響。

2.1.2 直方圖算法

1. 直方圖算法

直方圖算法的基本思想是將連續(xù)的特征離散化為 k 個(gè)離散特征，同時(shí)構(gòu)造一個(gè)寬度為 k 的直方圖用于統(tǒng)計(jì)信息（含有 k 個(gè) bin）。利用直方圖算法我們無(wú)需遍歷數(shù)據(jù)，只需要遍歷 k 個(gè) bin 即可找到最佳分裂點(diǎn)。

我們知道特征離散化的具有很多優(yōu)點(diǎn)，如存儲(chǔ)方便、運(yùn)算更快、魯棒性強(qiáng)、模型更加穩(wěn)定等等。對(duì)于直方圖算法來(lái)說(shuō)最直接的有以下兩個(gè)優(yōu)點(diǎn)（以 k=256 為例）：

• 內(nèi)存占用更小：XGBoost 需要用 32 位的浮點(diǎn)數(shù)去存儲(chǔ)特征值，并用 32 位的整形去存儲(chǔ)索引，而 LightGBM 只需要用 8 位去存儲(chǔ)直方圖，相當(dāng)于減少了 1/8；
• 計(jì)算代價(jià)更小：計(jì)算特征分裂增益時(shí)，XGBoost 需要遍歷一次數(shù)據(jù)找到最佳分裂點(diǎn)，而 LightGBM 只需要遍歷一次 k 次，直接將時(shí)間復(fù)雜度從 O(#data * #feature) 降低到 O(k * #feature) ，而我們知道 #data >> k 。

雖然將特征離散化后無(wú)法找到精確的分割點(diǎn)，可能會(huì)對(duì)模型的精度產(chǎn)生一定的影響，但較粗的分割也起到了正則化的效果，一定程度上降低了模型的方差。

2. 直方圖加速

在構(gòu)建葉節(jié)點(diǎn)的直方圖時(shí)，我們還可以通過(guò)父節(jié)點(diǎn)的直方圖與相鄰葉節(jié)點(diǎn)的直方圖相減的方式構(gòu)建，從而減少了一半的計(jì)算量。在實(shí)際操作過(guò)程中，我們還可以先計(jì)算直方圖小的葉子節(jié)點(diǎn)，然后利用直方圖作差來(lái)獲得直方圖大的葉子節(jié)點(diǎn)。

3. 稀疏特征優(yōu)化

XGBoost 在進(jìn)行預(yù)排序時(shí)只考慮非零值進(jìn)行加速，而 LightGBM 也采用類似策略：只用非零特征構(gòu)建直方圖。