12.1 項目分析

矩陣鍵盤，是一種在節省端口的前提下控制大量按鍵的一種方法，對于傳統的獨立對地鍵盤，一個按鍵就需要占用一個單片機IO口，雖然有時候會加一些擴展芯片之類的用于一個端口控制多個按鍵，但是電路結構比較復雜，矩陣鍵盤則是一種盡可能的既不用驅動芯片又能最大限度的使用大量按鍵的方法，一個a行b列的矩陣鍵盤，它所占用的端口數量是a+b個端口，所控制的按鍵數量則是a×b個按鍵，比如常見的4×4矩陣鍵盤只需要占用8個端口就可以控制16個按鍵，矩陣鍵盤的接法如下圖所示。

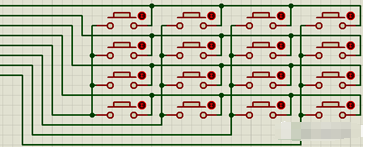
從圖中可以看出，每一列的按鍵取一端接在一起，每一行的按鍵取按鍵的另一列接在一起，這樣就會引出四條行掃描線和列掃描線，假設某個端口產生了低電平，那么對應的就會有四個按鍵變成了獨立對地鍵盤，當這四個鍵按下的時候，對應的端口電平就會拉低，所以矩陣鍵盤的按鍵檢測主要就是進行掃描檢測，在短暫的時間內不停的掃描鍵盤，可以根據行掃描判斷，也可以根據列掃描判斷，矩陣鍵盤的識別主要有以下幾種判斷方法：

算法1 ：對矩陣鍵盤的行（或者列）不停的掃描，然后檢測對應的列（或者行），當掃描的頻率超過人的反應時間時，便不會被感覺出來，但是這種方法的優點是程序編寫較為簡單，但是代碼很長，且浪費CPU的資源。

算法2： 對矩陣鍵盤的列（或者行）全部賦低電平，然后判斷是否有行（或者列）的端口有低電平產生，沒有，證明按鍵沒有被按下，如果有，那么此時將端口對應的數據存放入一個變量，并同時將列（或者行）的低電平轉移到行（或者列）上，此時列（或者行）必然也會有一個低電平的端口，將這時候的數據存放入第二個變量，最后，撤銷所有的低電平，將兩個變量的數據相加，則必然會得出所有按鍵值的其中一個，那么這個按鍵值所對應的按鍵必然就是按下的按鍵，這種算法比較復雜，編程或者理解起來比較困難，但是代碼短，節省CPU資源。

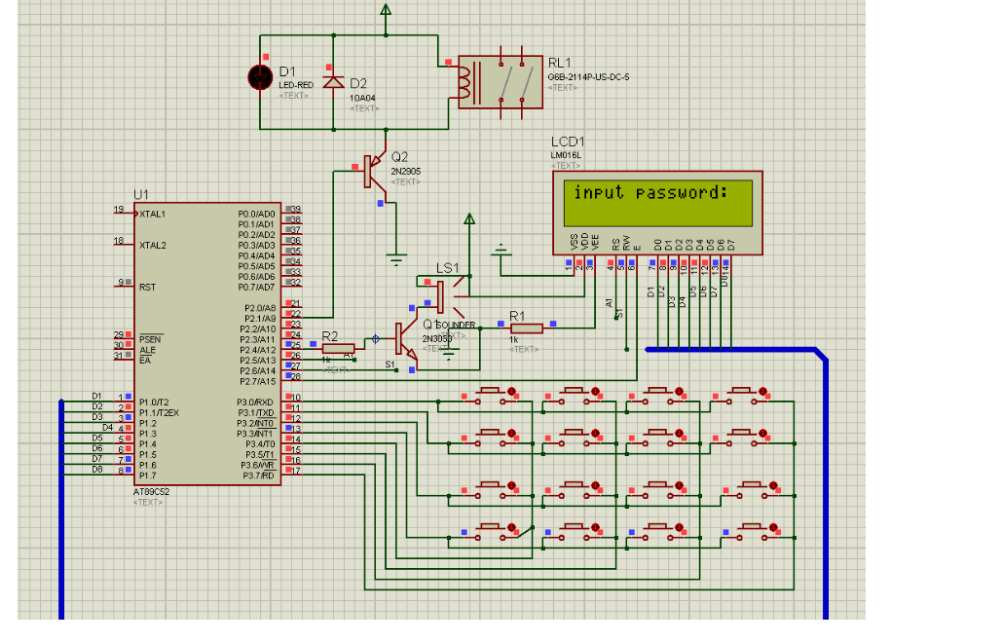
12.2 原理圖

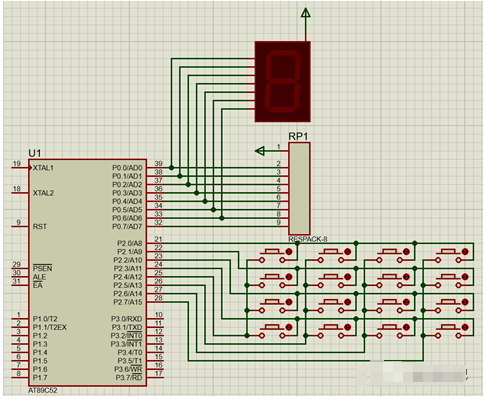
現在我們以原理圖為例，實現如下功能，用0~F代表按鍵的編號，按下某個按鍵后，在數碼管上顯示按鍵的編號（要求采用算法2方式實現）。

**12.3 **源代碼

/*********************************************************************************************************
                頭    文    件    引    用
*********************************************************************************************************/
#include <reg51.h>                                            //導入51單片機頭文件
#include <intrins.h>
/*********************************************************************************************************
              數    據    類    型    定    義
*********************************************************************************************************/
#define u8 unsigned char                                        //定義無符號字符型數據(0~255)
#define u16 unsigned int                                        //定義無符號整型數據(0~65535)
/********************************************************
Name    :KEY_Scan
Function  :鍵盤掃描
Paramater  :None
Return    :None
********************************************************/
void KEY_Scan()
{
  u8 x, y ;
  u8 TAB[] = { 0x40, 0x79, 0x24, 0x30, 0x19, 0x12, 0x02, 0x78, 0x00, 0x10, 0x08, 0x03, 0x46, 0x21, 0x06, 0x0E } ;
  P2 = 0xF0 ;
  if( P2!=0xF0 )
  {
    x = P2 ;
    P2 = 0x0F ;
    if( P2!=0x0F )
    {
      y = P2 ;
      switch( x+y )
      {
        case 0xEE:  P0 = TAB[ 0 ] ;    break ;
        case 0xDE:  P0 = TAB[ 1 ] ;    break ;
        case 0xBE:  P0 = TAB[ 2 ] ;    break ;
        case 0x7E:  P0 = TAB[ 3 ] ;    break ;
        case 0xED:  P0 = TAB[ 4 ] ;    break ;
        case 0xDD:  P0 = TAB[ 5 ] ;    break ;
        case 0xBD:  P0 = TAB[ 6 ] ;    break ;
        case 0x7D:  P0 = TAB[ 7 ] ;    break ;
        case 0xEB:  P0 = TAB[ 8 ] ;    break ;
        case 0xDB:  P0 = TAB[ 9 ] ;    break ;
        case 0xBB:  P0 = TAB[ 10 ] ;  break ;
        case 0x7B:  P0 = TAB[ 11 ] ;  break ;
        case 0xE7:  P0 = TAB[ 12 ] ;  break ;
        case 0xD7:  P0 = TAB[ 13 ] ;  break ;
        case 0xB7:  P0 = TAB[ 14 ] ;  break ;
        case 0x77:  P0 = TAB[ 15 ] ;  break ;
      }
    }
  }
}
/*********************************************************************************************************
                    主    函    數
*********************************************************************************************************/
void main()
{
  while( 1 )
  {
    KEY_Scan() ;
  }
}

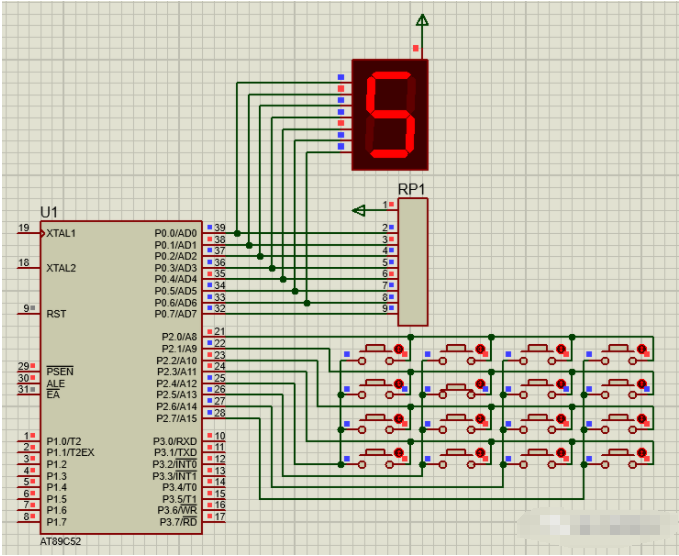
12.4 仿真效果