1
阿倫尼斯計算模型
物理加速模型是基于對產品失效過程的物理化學解釋而提出的。一種典型的物理加速模型是阿倫尼斯(Arrhenius)模型,阿倫尼斯模型適用于單純考慮熱效應試驗的加速模型,當溫度是影響產品老化及使用壽命的絕對因素時,采用該加速模型來模擬整個壽命周期的可靠性表現。
加速因子公式表達:
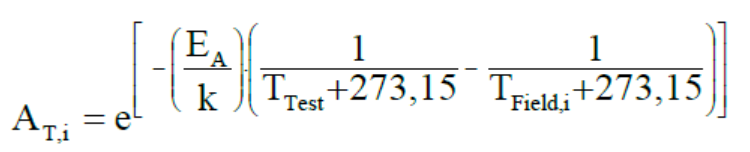
其中公式中各個參數代表的含義解釋如下:
AT,i:加速因子,在所有的加速模型中都是表達一個含義,也就相當于加速系數,計算出他就能將整個壽命周期時間轉換成加速試驗的時間;就是我們要算出來的每個溫度點下的加速因子,比如i為1,則根據譜圖第一行來算出該條件下的加速因子,具體的含義就是比如說AT,1算出來為5000,則意味著如果想代替在-40°C 下工作的占6%比例的這段壽命時間,則等價的試驗就是在T pruf下工作8212.5/5000個小時。e: 就是一個常數,2.71828,在excel里面這里對應的就是exp函數。
Ea:是析出故障的耗費能量,又稱激活能。不同產品的激活能是不一樣的。一般來說,激活能的值在0.3ev~1.2ev之間;此數值也是由主機廠提供,這里給出的是0.45eV。
K:是玻爾茲曼常數,其值為8.617385×10-5 ev/K;
Ttest:測試條件下(加速狀態下)的溫度值。此處的溫度值是絕對溫度值,以K(開爾文)作單位;就是指你想在什么溫度條件下進行該加速試驗,通常情況為了達到最快的加速且不會損壞產品,我們會選擇溫度譜圖中的最高溫度,即80°C。
Tfield:是使用條件下(非加速狀態下)的溫度值。此處的溫度值是絕對溫度值,以K(開爾文)作單位
很多人不知道活化能Ea應該選取那個值?其實不同的Ea對應了不同的失效機理,下面表格是一些電子元器件在經驗累積得到推薦值。
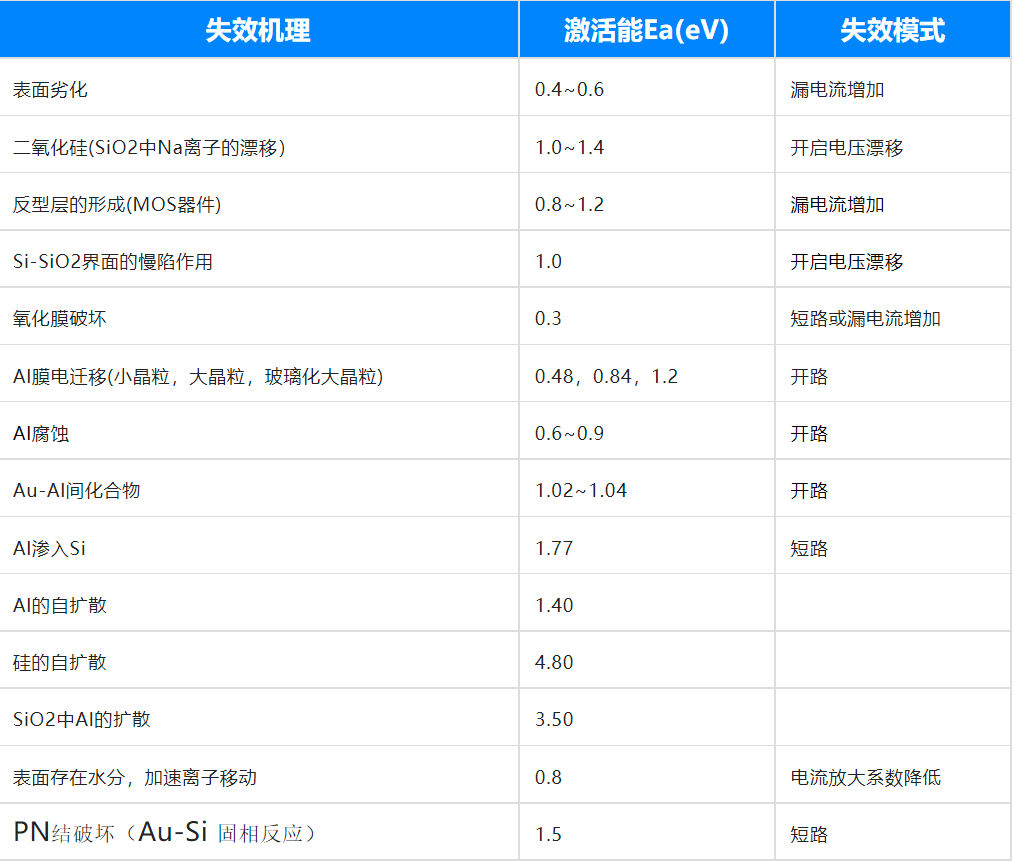
但是我們在做產品溫度加速時,一般是針對整系統,那么Ea應該如何選取。通常情況下,根據經驗Ea可選取0.5~0.7eV.比如戴爾電腦對PC的Ea選取0.6eV,這個值也是多次試驗的出來的平均值。這個Ea選取主要針對但應力加速時,如果有2個應力以上,則無需考慮,可以通過試驗結果計算出來。
阿倫尼斯模型有下述特點:
(1)該模型反映的是產品某特性量與激活能和所施加應力的關系;
(2)阿倫尼斯模型使用的壽命與溫度的表達形式及加速因子都是基于退化量相同導出的。這就為加速壽命試驗提供了另外一條途徑,即利用某性能參數或特征量退化數據對產品的可靠性進行評定、推斷。
(3)從公式中可以看出,激活能越大,加速系數也越大,越容易被加速失效,加速試驗效果越明顯;
(4)在激活能確定的情況下,溫度差越大,加速系數也越大;
【實操計算】:
案例:某一客戶需要對產品做105℃的高溫測試。據以往的測試經驗,此種產品的激活能Ea取0.68最佳。對產品的使用壽命要求是10年,現可供測試的樣品有5個。若同時對5個樣品進行測試,需測試多長時間才能滿足客戶要求?
解:
AF=EXP(Ea/k*(1/Tnormal-1/Tfeild))=exp(0.68/K*(1/((25+273)-1/(105+273)))=262
T測=Life/AF=10*365*24/262=333.73h
2
科芬曼森模型
科芬-曼森模型是適用于溫度沖擊試驗的加速模型,反映了溫度交變應力作用下的疲勞破壞。該方法成功地模擬了在溫度交變應力作用下焊點的裂紋擴展過程。
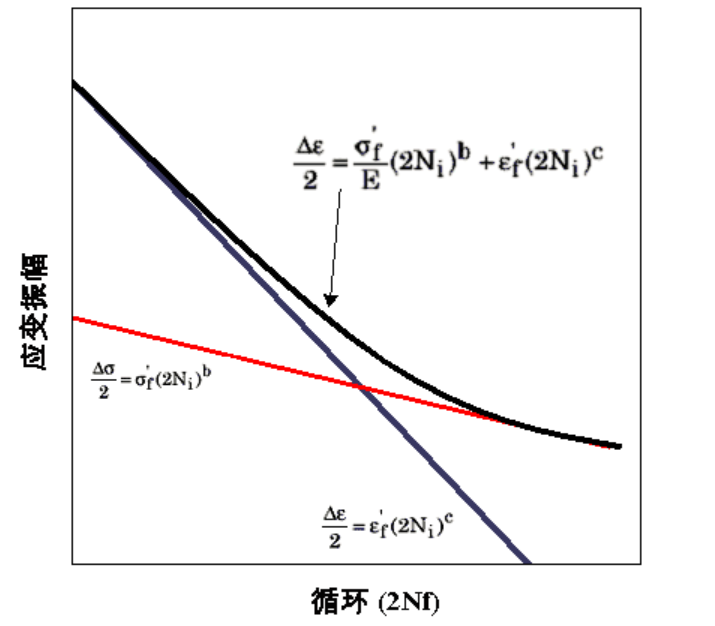
公式表達 :
ΔTtest:測試循環的高低溫之間的差值;
Acm:該模型的加速因子;
ΔTfild:溫度譜中平均溫度差異,一般產品終端會給出明確值;一般由主機廠給出,這里是40°C.
C:科芬-曼森指數,它指的是溫度變化的加速率常數,不同的失效類型對應不同的值;一般由主機廠指定,它指的是溫度變化的加速率常數,不同的失效類型對應不同的值.據我所知,大眾和奔馳對該值都指定為2.5。
公式二:
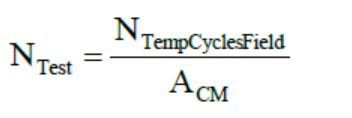
Ntf:實際使用大概的循環數;
Ntest:需要測試的循環數;
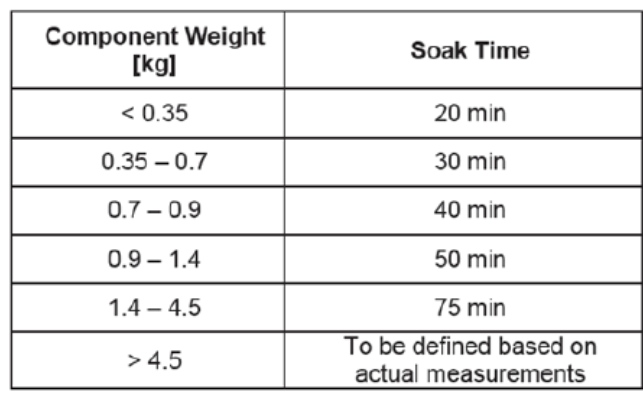
知道循環數,最高溫度(T max) 及最低溫度(T min)后,接下來就是該公式應用起來最困難的部分,即怎么確定溫度變化速率以及在每個溫度點上的停留時間,有些情況下主機廠會直接指定相關參數,比如下表就是一家主機廠給出的數據,要求我們根據樣品的質量來決定在每個溫度點的停留時間。
最后,在確定溫度變化速率t speed)以及在每個溫度點上的停留時間(t holding time)后,就可以根據下面公式算出每個循環所需要的時間,再乘以上面算出的總循環數,就能確定該溫度循環試驗所需耗費的總時間了。
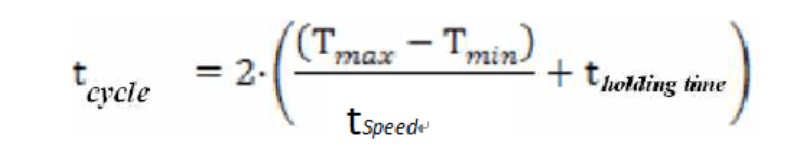
【實操計算】
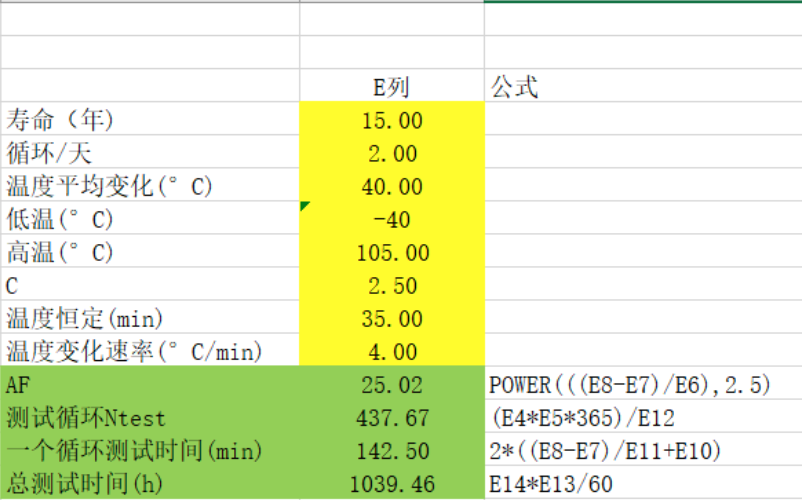
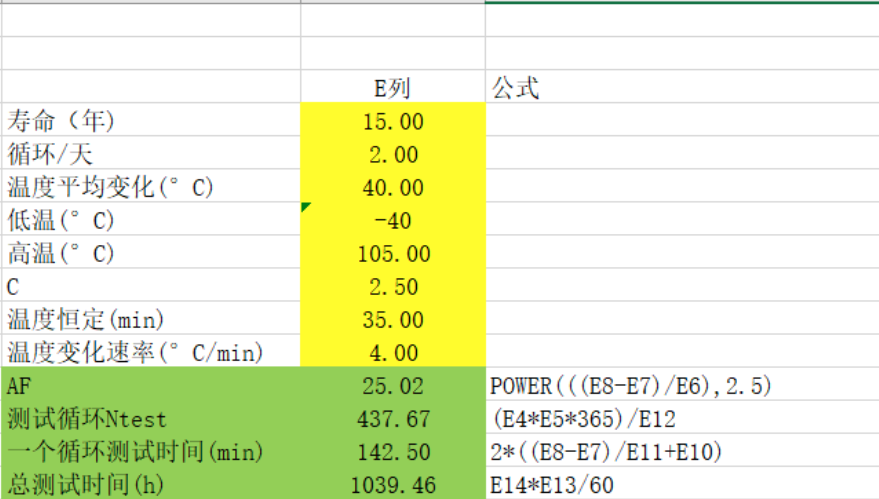
假設一種產品在實際使用過程中,每天會經過兩個溫度交變的循環,預計使用壽命是15年,失效因數是2.5,溫度變化范圍是-40°C,高溫是105°C,平均溫度變化是40°C,根據經驗,高低溫到達的恒定的時間是35min,試計算如果采用循環加速壽命需要多少循環,多長時間?
Excel表格計算公式如下:
3
勞森模型Lawson
在阿倫紐斯模型的基礎上引入濕度應力的影響,就是勞森模型。
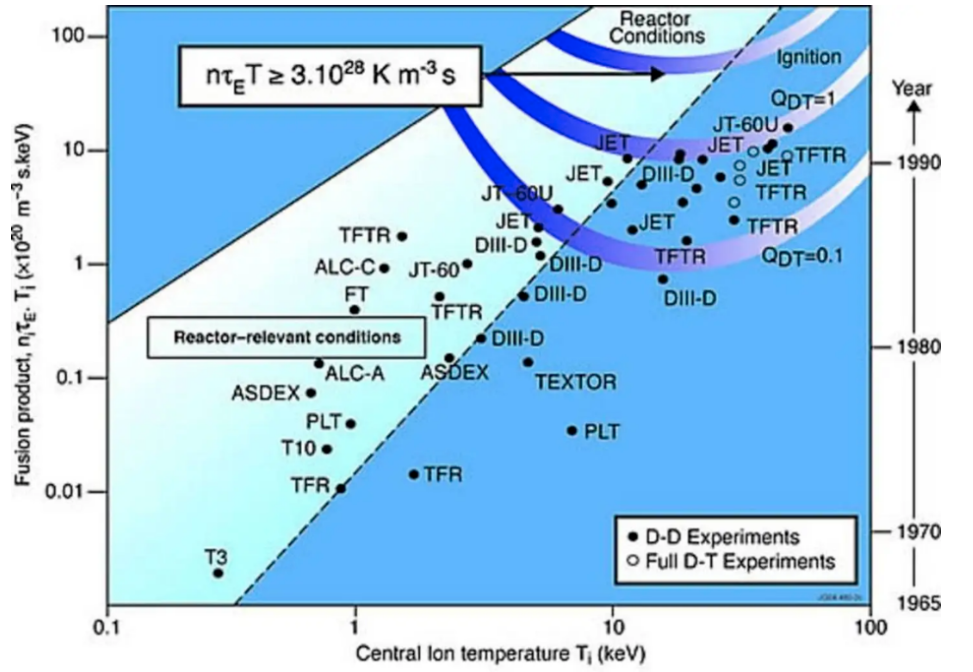
公式如下:
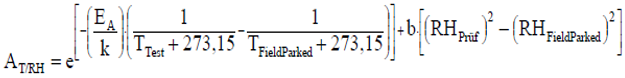
AT/RH:加速因子
b:常數(b = 5.57 x 10^-4)
EA:活化能(EA = 0,4 eV)
K:是玻爾茲曼常數,其值為8.617385×10-5 ev/K;
Ttest:測試條件下(加速狀態下)的溫度值。此處的溫度值是絕對溫度值,以K(開爾文)作單位;
Tfield:是使用條件下(非加速狀態下)的溫度值。此處的溫度值是絕對溫度值,以K(開爾文)作單位
RHTest:測試期間的相對濕度,比如這里我們選擇93%RH。
RHFieldParked:實驗箱內的平均相對濕度(%),由主機廠給出;
因此根據上面的參數,可以算出要想加速到65°C,93%RH則對應的加速因子AT/RH為105.04。接下來再使用該公式來計算對應的試驗時間t pruf:
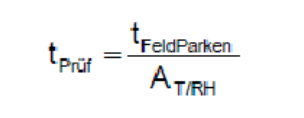
tFeldParken:就是指在主機廠要求的壽命期間內汽車不運行的時間,這里以極限的15年來考慮,即按照15年該車都不運行的狀態來考慮此時間,15*365*24=131400h。
因此再結合上面算出的加速因子可以得知要想在65°C,93%RH的條件下來加速該試驗,則對應的試驗時間約為1251小時。
4
隨機振動試驗加速因子
振動試驗是指評定產品在預期的使用環境中抗振能力而對受振動的實物或模型進行的試驗。根據施加的振動載荷的類型把振動試驗分為正弦振動試驗和隨機振動試驗兩種。
是模擬產品在運輸、安裝及使用環境下所遭遇到的各種振動環境影響,用來確定產品是否能承受各種環境振動的能力。振動試驗是評定元器件、零部件及整機在預期的運輸及使用環境中的抵抗能力。
在標準GB/T 21563-2008 軌道交通 機車車輛設備 沖擊和振動試驗中給出了試驗時間和壽命時間與試驗加速度和實際應力加速度的對應關系。
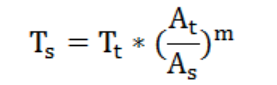
Ts:運行壽命/時間;Tt:試驗時間;As:運行加速度;At:試驗加速度;M:金屬材料選擇4。
可以得到如下公式:
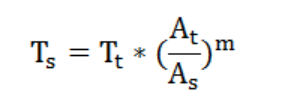
對于振動加速度,如果不加說明,一般指振動的峰值,即g。對隨機信號,一般是取一段時間計算均方根的加速度,即g(RMS),rms是均方根值(有效值)的意思。
例如某產品進行隨機振動試驗,加速度均方根值為0.7 grms,振動時間是10 h;如果實際產品24 h處理工作狀態,所面臨的振動加速度是0.08 grms;可以計算出該產品耐振動的運行時間是Ts=10 h*(0.7/0.08)4=58 618 h≈6.5年。
5
艾琳模型-電壓應力加速因子
產品除了環境應力的作用外,電應力的作用也不可忽視。電應力也會促使器件內部產生離子遷移、質量遷移等,造成短路、絕緣擊穿短路失效等。
器件在電壓、電流或功率等電應力作用下,應力越強、失效速率越快,器件壽命越短。Eyring模型是Arrhenius模型的擴展,用于溫度和電壓同時加速的試驗項目。
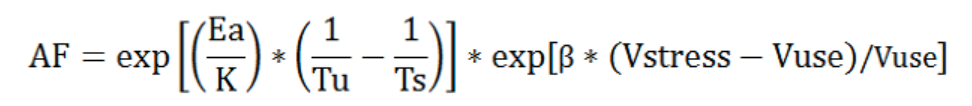
β:電壓加速常數(0.5≤β≤1.0,根據不同失效機理,默認值為1.0);Vstress:試驗時應力電壓(Stress voltage);Vuse:正常使用電壓(Operating voltage)
從艾琳模型模型中的電應力加速因子計算模型可知,只有正向的電壓才有加速應力,即試驗電壓要高于額定電壓。例如:某電子產品額定輸入電壓為220 Vac,試驗時輸入電壓為250 Vac。計算出AF(v)=1.12。
6
結束語
加速壽命試驗技術具有效率高,成本低,對高可靠、長壽命產品的定壽延壽研究具有重要的應用價值。目前加速壽命試驗技術在汽車領域應用都較為廣泛,并取得了一定研究成果。如汽車儀表、LED等都形成了各自的壽命評估標準。隨著研究的不斷深入,加速壽命試驗技術在各個領域將有廣闊應用前景。
審核編輯:劉清
-
led
+關注
關注
242文章
23338瀏覽量
662238 -
RMS
+關注
關注
2文章
139瀏覽量
35862 -
額定電壓
+關注
關注
0文章
334瀏覽量
14373
原文標題:淺談可靠性加速實驗的理論依據
文章出處:【微信號:心植桂冠,微信公眾號:心植桂冠】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
半導體封裝的可靠性測試及標準
提升產品穩定性:可靠性設計的十大關鍵要素

PCB高可靠性化要求與發展——PCB高可靠性的影響因素(上)
深入了解IXYS固態繼電器:可靠性與應用領域的完美結合
汽車功能安全與可靠性的關系

請問FATFS文件系統可靠性如何?
STO_PLL_CalcAvrgMecSpeed01Hz函數中以下代碼的理論依據是什么?
L6235Q的FWD/REV引腳輸入PWM波可以進行旋轉方向和調速的理論依據?
提升開關電源可靠性:全面了解測試項目與標準
天狼芯半導體上海車規級可靠性實驗中心正式啟用!
可靠性測試中HALT實驗與HASS實驗的區別

如何確保IGBT的產品可靠性




 簡單了解下可靠性加速實驗的理論依據
簡單了解下可靠性加速實驗的理論依據










評論