前言
最近 AI 繪圖非常的火,其背后用到的核心技術之一就是 Diffusion Model(擴散模型),雖然想要完全弄懂 Diffusion Model 和其中復雜的公式推導需要掌握比較多的前置數學知識,但這并不妨礙我們去理解其原理。接下來會以筆者所理解的角度去講解什么是 Diffusion Model。
什么是 Diffusion Model
前向 Diffusion 過程
Diffusion Model 首先定義了一個前向擴散過程,總共包含T個時間步,如下圖所示:
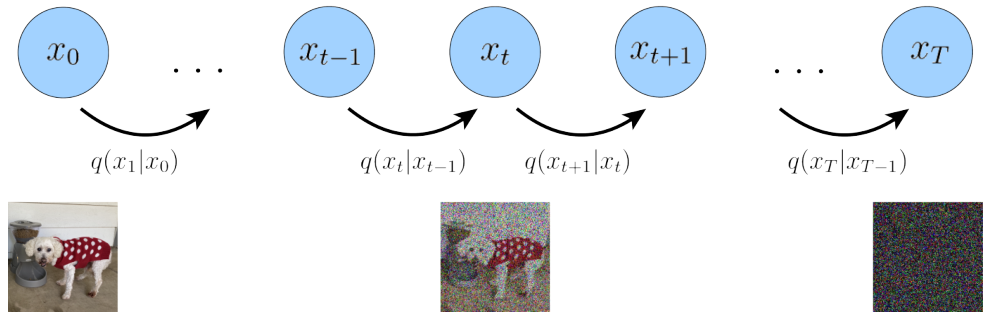
最左邊的藍色圓圈 x0 表示真實自然圖像,對應下方的狗子圖片。
最右邊的藍色圓圈 xT 則表示純高斯噪聲,對應下方的噪聲圖片。
最中間的藍色圓圈 xt 則表示加了噪聲的 x0 ,對應下方加了噪聲的狗子圖片。
箭頭下方的 q(xt|xt-1) 則表示一個以前一個狀態 xt-1 為均值的高斯分布,xt 從這個高斯分布中采樣得到。
所謂前向擴散過程可以理解為一個馬爾可夫鏈(見參考資料[7]),即通過逐步對一張真實圖片添加高斯噪聲直到最終變成純高斯噪聲圖片。
那么具體是怎么添加噪聲呢,公式表示如下:
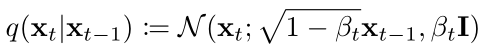
也就是每一時間步的 xt 是從一個,以 1-βt 開根號乘以 xt-1 為均值,βt為方差的高斯分布中采樣得到的。
其中βt, t ∈ [1, T] 是一系列固定的值,由一個公式生成。
在參考資料 [2] 中設置 T=1000, β1=0.0001, βT=0.02,并通過一句代碼生成所有 βt 的值:
# https://pytorch.org/docs/stable/generated/torch.linspace.html betas = torch.linspace(start=0.0001, end=0.02, steps=1000)
然后在采樣得到 xt 的時候并不是直接通過高斯分布 q(xt|xt-1) 采樣,而是用了一個重參數化的技巧(詳見參考資料[4]第5頁)。
簡單來說就是,如果想要從一個任意的均值 μ 方差 σ^2 的高斯分布中采樣
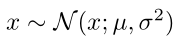
可以首先從一個標準高斯分布(均值0,方差1)中進行采樣得到 ε,
然后 μ + σ·ε 就等價于從任意高斯分布中進行采樣的結果。公式表示如下:
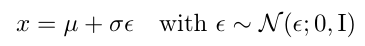
接著回來看具體怎么采樣得到噪聲圖片 xt呢,
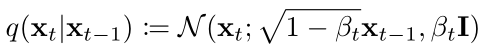
也是首先從標準高斯分布中采樣,接著乘以標準差再加上均值 ,偽代碼如下:
# https://pytorch.org/docs/stable/generated/torch.randn_like.html betas = torch.linspace(start=0.0001, end=0.02, steps=1000) noise = torch.randn_like(x_0) xt = sqrt(1-betas[t]) * xt-1 + sqrt(betas[t]) * noise
然后前向擴散過程還有個屬性,就是可以直接從 x0 采樣得到中間任意一個時間步的噪聲圖片 xt,公式如下:
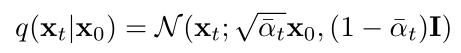
其中的 αt 表示:
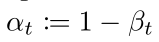
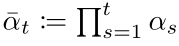
具體怎么推導出來的可以看參考資料[4] 第11頁,偽代碼表示如下:
betas = torch.linspace(start=0.0001, end=0.02, steps=1000) alphas = 1 - betas # cumprod 相當于為每個時間步 t 計算一個數組 alphas 的前綴乘結果 # https://pytorch.org/docs/stable/generated/torch.cumprod.html alphas_cum = torch.cumprod(alphas, 0) alphas_cum_s = torch.sqrt(alphas_cum) alphas_cum_sm = torch.sqrt(1 - alphas_cum) # 應用重參數化技巧采樣得到 xt noise = torch.randn_like(x_0) xt = alphas_cum_s[t] * x_0 + alphas_cum_sm[t] * noise
通過上述的講解,讀者應該對 Diffusion Model 的前向擴散過程有比較清晰的理解了。
不過我們的目的不是要做圖像生成嗎?
現在只是從數據集中的真實圖片得到一張噪聲圖,那具體是怎么做圖像生成呢?
反向 Diffusion 過程
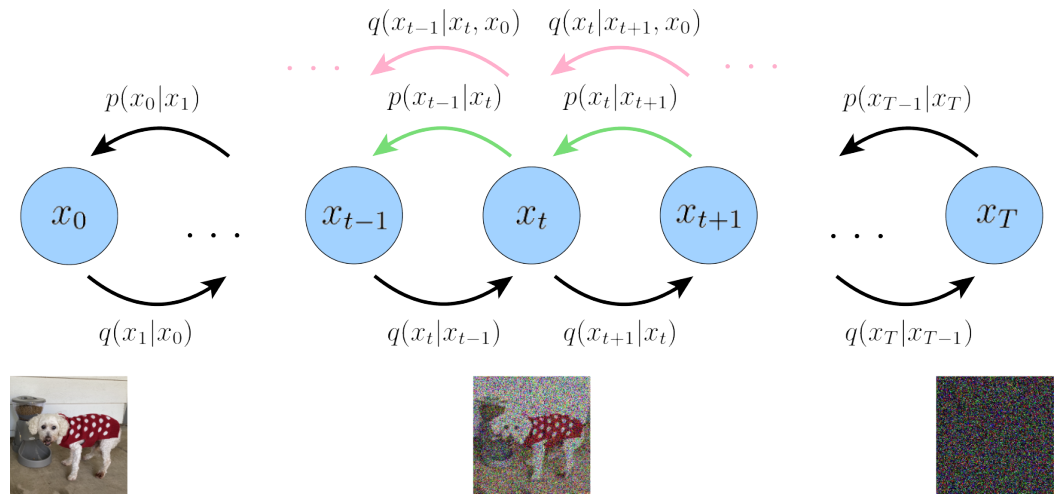
反向擴散過程 q(xt-1|xt, x0) (看粉色箭頭)是前向擴散過程 q(xt|xt-1) 的后驗概率分布。
和前向過程相反是從最右邊的純高斯噪聲圖,逐步采樣得到真實圖像 x0。
后驗概率 q(xt-1|xt, x0) 的形式可以根據貝葉斯公式推導得到(推導過程詳見參考資料[4]第12頁):
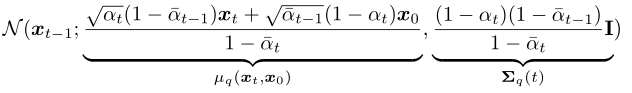
也是一個高斯分布。
其方差從公式上看是個常量,所有時間步的方差值都是可以提前計算得到的:
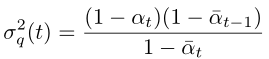
計算偽代碼如下:
betas = torch.linspace(start=0.0001, end=0.02, steps=1000) alphas = 1 - betas alphas_cum = torch.cumprod(alphas, 0) alphas_cum_prev = torch.cat((torch.tensor([1.0]), alphas_cum[:-1]), 0) posterior_variance = betas * (1 - alphas_cum_prev) / (1 - alphas_cum)
然后看均值的計算,
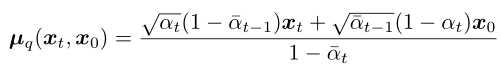
對于反向擴散過程,在采樣生成 xt-1 的時候 xt 是已知的,而其他系數都是可以提前計算得到的常量。
但是現在問題來了,在真正通過反向過程生成圖像的時候,x0 我們是不知道的,因為這是待生成的目標圖像。
好像變成了雞生蛋,蛋生雞的問題,那該怎么辦呢?
Diffusion Model 訓練目標
當一個概率分布q 求解困難的時候,我們可以換個思路(詳見參考資料[5,6])。
通過人為構造一個新的分布 p,然后目標就轉為縮小分布 p 和 q 之間差距。
通過不斷修改 p 的參數去縮小差距,當 p 和 q 足夠相似的時候就可以替代 q 了。
然后回到反向 Diffusion 過程,由于后驗分布 q(xt-1|xt, x0) 沒法直接求解。

那么我們就構造一個高斯分布 p(xt-1|xt)(見綠色箭頭),讓其方差和后驗分布 q(xt-1|xt, x0) 一致:
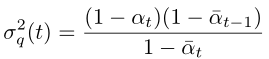
而其均值則設為:
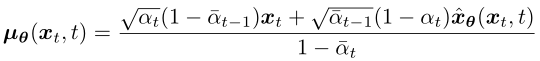
和 q(xt-1|xt, x0) 的區別在于,x0 改為 xθ(xt, t) 由一個深度學習模型預測得到,模型輸入是噪聲圖像 xt 和時間步 t 。
然后縮小分布 p(xt-1|xt) 和 q(xt-1|xt, x0) 之間差距,變成優化以下目標函數(推導過程詳見參考資料[4]第13頁):
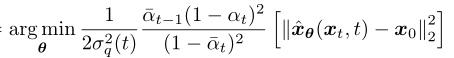
但是如果讓模型直接從 xt 去預測 x0,這個擬合難度太高了,我們再繼續換個思路。
前面介紹前向擴散過程提到,xt 可以直接從 x0 得到:
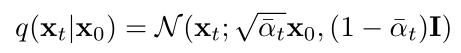
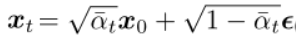
將上面的公式變換一下形式:
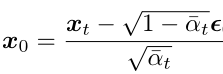
代入上面 q(xt-1|xt, x0) 的均值式子中可得(推導過程詳見參考資料[4]第15頁):
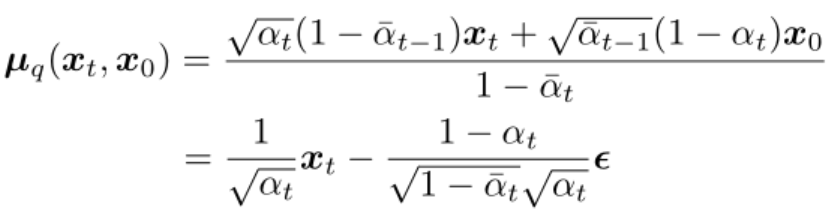
觀察上述變換后的式子,發現后驗概率 q(xt-1|xt, x0) 的均值只和 xt 和前向擴散時候時間步 t 所加的噪聲有關。
所以我們同樣對構造的分布 p(xt-1|xt) 的均值做一下修改:
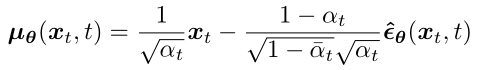
將模型改為去預測在前向時間步 t 所添加的高斯噪聲 ε,模型輸入是 xt 和 時間步 t:
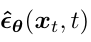
接著優化的目標函數就變為(推導過程詳見參考資料[4]第15頁):
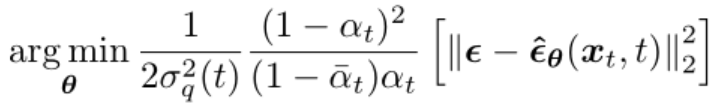
然后訓練過程算法描述如下,最終的目標函數前面的系數都去掉了,因為是常量:

可以看到雖然前面的推導過程很復雜,但是訓練過程卻很簡單。
首先每個迭代就是從數據集中取真實圖像 x0,并從均勻分布中采樣一個時間步 t,
然后從標準高斯分布中采樣得到噪聲 ε,并根據公式計算得到 xt。
接著將 xt 和 t 輸入到模型讓其輸出去擬合預測噪聲 ε,并通過梯度下降更新模型,一直循環直到模型收斂。
而采用的深度學習模型是類似 UNet 的結構(詳見參考資料[2]附錄B)。
訓練過程的偽代碼如下:
betas = torch.linspace(start=0.0001, end=0.02, steps=1000)
alphas = 1 - betas
alphas_cum = torch.cumprod(alphas, 0)
alphas_cum_s = torch.sqrt(alphas_cum)
alphas_cum_sm = torch.sqrt(1 - alphas_cum)
def diffusion_loss(model, x0, t, noise):
# 根據公式計算 xt
xt = alphas_cum_s[t] * x0 + alphas_cum_sm[t] * noise
# 模型預測噪聲
predicted_noise = model(xt, t)
# 計算Loss
return mse_loss(predicted_noise, noise)
for i in len(data_loader):
# 從數據集讀取一個 batch 的真實圖片
x0 = next(data_loader)
# 采樣時間步
t = torch.randint(0, 1000, (batch_size,))
# 生成高斯噪聲
noise = torch.randn_like(x_0)
loss = diffusion_loss(model, x0, t, noise)
optimizer.zero_grad()
loss.backward()
optimizer.step()
Diffusion Model 生成圖像過程
模型訓練好之后,在真實的推理階段就必須從時間步 T 開始往前逐步生成圖片,算法描述如下:

一開始先生成一個從標準高斯分布生成噪聲,然后每個時間步 t,將上一步生成的圖片 xt 輸入模型模型預測出噪聲。接著從標準高斯分布中采樣一個噪聲,根據重參數化技巧,后驗概率的均值和方差公式,計算得到 xt-1,直到時間步 1 為止。
改進 Diffusion Model
文章 [3] 中對 Diffusion Model 提出了一些改進點。
對方差 βt 的改進
前面提到 βt 的生成是將一個給定范圍均勻的分成 T 份,然后每個時間步對應其中的某個點:
betas = torch.linspace(start=0.0001, end=0.02, steps=1000)
然后文章 [3] 通過實驗觀察發現,采用這種方式生成方差 βt 會導致一個問題,就是做前向擴散的時候到靠后的時間步噪聲加的太多了。
這樣導致的結果就是在前向過程靠后的時間步,在反向生成采樣的時候并沒有產生太大的貢獻,即使跳過也不會對生成結果有多大的影響。
接著論文[3] 中就提出了新的 βt 生成策略,和原策略在前向擴散的對比如下圖所示:

第一行就是原本的生成策略,可以看到還沒到最后的時間步就已經變成純高斯噪聲了,
而第二行改進的策略,添加噪聲的速度就慢一些,看起來也更合理。
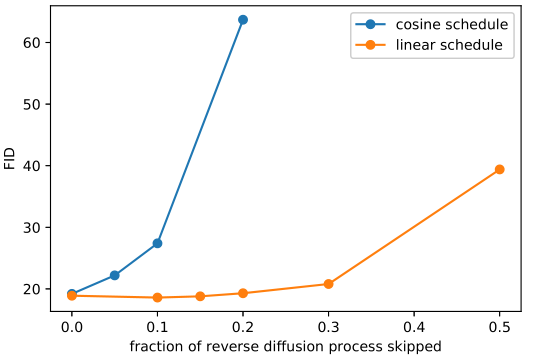
實驗結果表明,針對 imagenet 數據集 64x64 的圖片,原始的策略在做反向擴散的時候,即使跳過開頭的 20% 的時間步,都不會對指標有很大的影響。
然后看下新提出的策略公式:
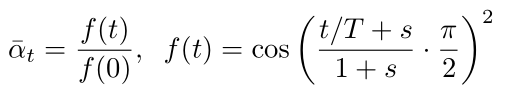
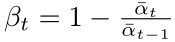
其中 s 設置為 0.008同時限制 βt最大值為 0.999,偽代碼如下:
T = 1000 s = 8e-3 ts = torch.arange(T + 1, dtype=torch.float64) / T + s alphas = ts / (1 + s) * math.pi / 2 alphas = torch.cos(alphas).pow(2) alphas = alphas / alphas[0] betas = 1 - alphas[1:] / alphas[:-1] betas = betas.clamp(max=0.999)
對生成過程時間步數的改進
原本模型訓練的時候是假定在 T個時間步下訓練的,在生成圖像的時候,也必須從 T 開始遍歷到 1 。而論文 [3] 中提出了一種不需要重新訓練就可以減少生成步數的方法,從而顯著提升生成的速度。
這個方法簡單描述就是,原來是 T 個時間步現在設置一個更小的時間步數 S ,將 S 時間序列中的每一個時間步 s 和 T時間序列中的步數 t 對應起來,偽代碼如下:
T = 1000
S = 100
start_idx = 0
all_steps = []
frac_stride = (T - 1) / (S - 1)
cur_idx = 0.0
s_timesteps = []
for _ in range(S):
s_timesteps.append(start_idx + round(cur_idx))
cur_idx += frac_stride
接著計算新的 β ,St 就是上面計算得到的 s_timesteps:
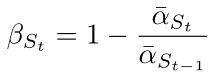
偽代碼如下:
alphas = 1 - betas
alphas_cum = torch.cumprod(alphas, 0)
last_alpha_cum = 1.0
new_betas = []
# 遍歷原來的 alpha 前綴乘序列
for i, alpha_cum in enumerate(alphas_cum):
# 當原序列 T 的索引 i 在新序列 S 中時,計算新的 beta
if i in s_timesteps:
new_betas.append(1 - alpha_cum / last_alpha_cum)
last_alpha_cum = alpha_cum
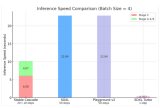
簡單看下實驗結果:
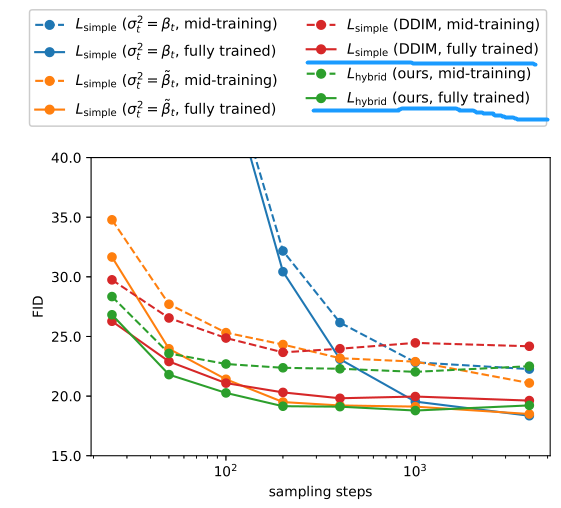
關注畫藍線的紅色和綠色實線,可以看到采樣步數從 1000 縮小到 100 指標也沒有降多少。
審核編輯:劉清
-
圖像處理
+關注
關注
27文章
1300瀏覽量
56841
原文標題:一文弄懂 Diffusion Model
文章出處:【微信號:GiantPandaCV,微信公眾號:GiantPandaCV】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于擴散模型的圖像生成過程

Stable Diffusion的完整指南:核心基礎知識、制作AI數字人視頻和本地部署要求
Stability AI開源圖像生成模型Stable Diffusion
從一個名為DDPM的模型說起
大腦視覺信號被Stable Diffusion復現圖像!
一文讀懂Stable Diffusion教程,搭載高性能PC集群,實現生成式AI應用

使用OpenVINO?在算力魔方上加速stable diffusion模型
優化 Stable Diffusion 在 GKE 上的啟動體驗
樹莓派能跑Stable Diffusion了?
Stable Diffusion的完整指南:核心基礎知識、制作AI數字人視頻和本地部署要求
DDFM:首個使用擴散模型進行多模態圖像融合的方法

NeurIPS 2023 | 擴散模型解決多任務強化學習問題

Stability AI試圖通過新的圖像生成人工智能模型保持領先地位




 什么是Diffusion Model?Diffusion Model生成圖像過程
什么是Diffusion Model?Diffusion Model生成圖像過程
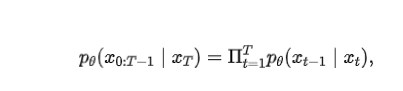











評論