傅里葉變換的提出讓人們看問題的角度從時域變成了頻域,多了一個維度。快速傅里葉變換算法的提出普及了傅里葉變換在工程領域的應用,在科學計算和數字信號處理等領域,離散傅里葉變換(DFT)至今依然是非常有效的工具之一。
比如下圖是一個幅度為1、頻率為2Hz的正弦波和它的離散傅里葉變換后的結果。
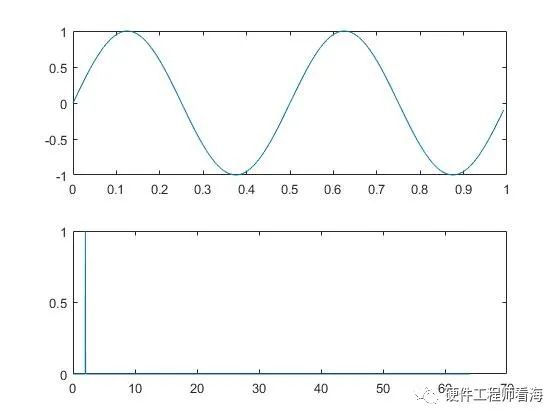
信噪比(SNR)是信號與噪聲的比率,它是衡量通信或模擬系統性能的重要指標之一,與傅里葉變換更是有千絲萬縷的聯系。在很多情況下,我們是通過傅里葉變換來評估信噪比,如果評估方法不對,很難的到我們期望的結果,經常會事與愿違。
求解SNR的過程,我們是用‘評估SNR’來描述,這就是說我們無法精確計算出SNR,只能進行評估,事實也是如此。
評估SNR的方法分為時域和頻域兩種。我們以一組離散樣本點為分析目標,看下如何評估SNR,及其誤區。
時域估計SNR
Xs(n)為信號序列,Xn(n)為噪聲序列,則信號X(n)=Xs(n)+Xn(n),是一組帶噪離散序列,在時域上評估X(n)的信噪比公式如下:
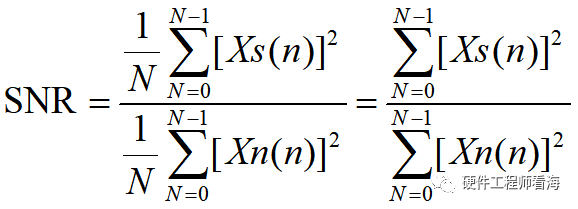
其意義為分別求取離散信號、噪聲功率和,計算二者之比。這里有個前提是,我們需要分離出信號與噪聲,然后才能求解,
然而問題也在于此,對于一段給定的離散時間序列,我們很難完全分離出信號和噪聲,所以時域評估SNR是有局限性的,而且不夠直觀,所以通常我們在頻域下求解。
頻域估計SNR
在頻域上的SNR計算原理和時域很接近,還是求信號功率與噪聲功率只比。最簡單的方法是在頻譜X(m)上設置閾值,閾值之上為信號,閾值之下為噪聲。這樣就會有閾值設置帶來的估計準確性問題,同時信號頻帶范圍內或多或少也會有噪聲疊加進來,在頻域計算SNR也是一個近似。

SNR以dB作為單位,SNR(dB)=10*log10(SNR)。
我們往往使用Matlab評估SNR,Matlab是非常強大的數學工具,其集成了SNR計算函數,如果應用不正確,誤差會非常大,無法得到預期結果,舉例如下。
下圖是一個幅度為1、頻率為2Hz的正弦波和它的離散傅里葉變換后的結果。

用Matlab SNR函數計算計算信噪比的結果如下,藍色為感興趣的信號成分,橙色為噪聲。這個頻域圖就可以表征SNR,橙色的噪聲數值越小、越低,說明信噪比越高、越好。即使紅色圓圈部分有一點噪聲,在評估單頻率成分信號的SNR時,這依然是一個非常有效的手段。
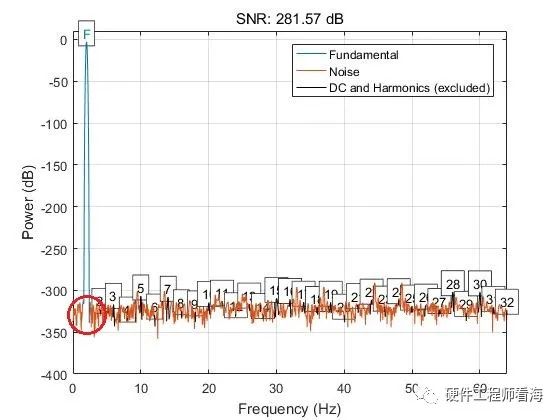
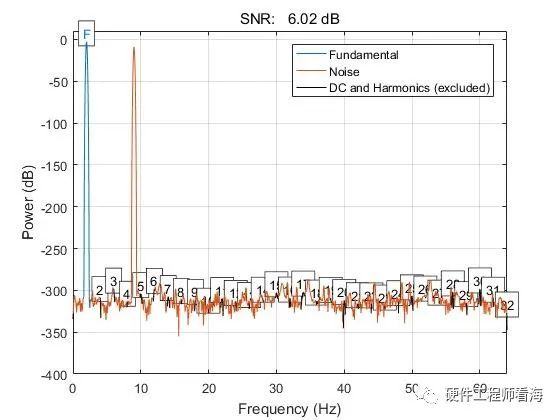
假如一信號x(n)=sin(4pit)+0.5sin(18pi*t),如下圖是一個幅度為1、頻率為2Hz的正弦波疊加幅度為0.5、頻率為9Hz的正弦波的結果。
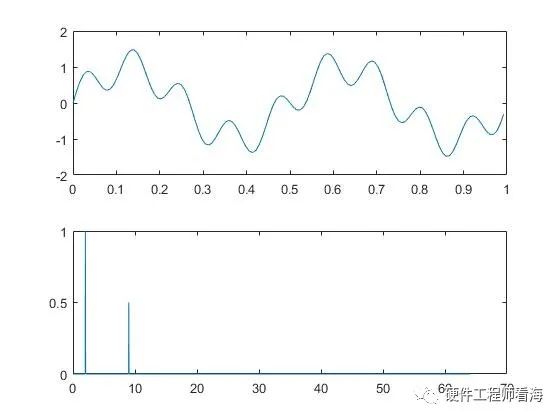
用Matlab SNR函數計算計算信噪比的結果如下,藍色為感興趣的信號成分,橙色為噪聲,matlab舍棄了頻率為9Hz、能量少的成分,只計算了2Hz信號的信噪比。
所以倘若我們的感興趣信號比較復雜,就不能直接用SNR函數直接計算。
所以我們一定要在理解DFT與SNR關系的基礎上,正確使用matlab才能得到期望的SNR結果。
在過采樣中,信噪比、ADC有效位數、過采樣率是有千絲萬縷的聯系,了解了基本的概念后,我們一步一步理解過采樣的原理。
審核編輯:劉清
-
信噪比
+關注
關注
3文章
260瀏覽量
28670 -
DFT
+關注
關注
2文章
231瀏覽量
22782 -
SNR
+關注
關注
3文章
196瀏覽量
24480 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42665
發布評論請先 登錄
相關推薦




 通過傅里葉變換來評估信噪比
通過傅里葉變換來評估信噪比












評論