文章來源:中國科學院理論物理研究所
原文作者:陳冬妮
1、從時間到空間
晶體在我們的日常生活中隨處可見,烹飪菜肴的食用鹽,晶瑩剔透的冰糖,水凝固后形成的冰,這些都是晶體。在微觀層面上,它們是由原子按一定規則有序排列的結構。事實上,晶體的存在是原子空間連續平移對稱性自發破缺的一種表現,這里的自發對稱性破缺指的是系統的基態比物理系統本身的對稱性低,系統的基態在哈密頓量的對稱性下不能保持不變。也就是說,原子的空間連續平移對稱性破缺,自組織的形成具有較低的空間離散平移對稱性的周期晶體結構。
由于物理定律在時間上也是連續平移對稱的,所以類比于三維空間中晶體的概念,麻省理工學院理論物理學家弗蘭克?威爾切克(Frank Wilczek)于2012年首次提出了時間晶體的概念:不同于空間晶體是在三維空間中形成重復的結構,時間晶體指的是系統的最低能狀態是系統處于重復運動的狀態,也就是說在時間上形成穩定的周期振蕩結構。自2012年時間晶體概念被提出起,是否可能在時間上打破對稱性,從而創造出“時間晶體” 成了理論和實驗物理學家們積極探索的問題。
2、離散時間晶體
2012年維爾切克提出了量子時間晶體模型[1],隨后,2013年加州大學的張翔團隊提出以離子阱為平臺實現量子時間晶體理論[2]。但是很快特里克?布魯諾 (Patrick Bruno)和渡邊悠樹(Haruki Watanabe)就針對他們的工作發表了幾篇文章[3,4],證明了在有限溫的平衡態情況下,只具有短程相互作用的多體物理系統,在熱力學極限下不存在量子時間晶體。因此在接下來的研究中,人們逐漸將關注點轉移到了在周期性調制的非平衡系統中。
2015 年克里斯托弗?薩查(Krzysztof Sacha) 發現在周期性驅動(Floquet)的冷原子系統中,系統的響應周期可以是外加驅動的周期的兩倍。他認為這正好體現出了離散時間平移對稱性的破缺[5]。隨后,離散時間晶體的理論得到快速發展。一個哈密頓量的周期驅動(Floquet)系統,當滿足以下三個條件時可以被稱為處于離散時間晶體階段[6,7]:1. 離散時間平移對稱性破缺:存在觀測量的周期不同于系統的驅動周期,也就是說,從變成,這里。2. 魯棒性:晶體必須堅固耐用,這意味著系統在特定范圍內存在外部波動時,當前狀態的離散時間晶體行為總能維持。3. 長時性:在熱力學極限滿足的情況下,這種周期為的倍周期性振蕩可以在無限長的時間內持續。
2016年,基于這個新概念進行了兩個非常重要的實驗。首先,馬里蘭大學的克里斯托弗·門羅(Christopher Monroe)團隊在射頻電磁場中捕獲了一連串的鐿-171離子,利用周期性激光驅動來操縱和觀察它們的自旋狀態。這導致它們以驅動周期的整數倍振蕩,是實現離散時間晶體的確定標志。并且這種亞諧波響應行為在受到外部微擾的情況下仍然成立[8]。同年,在哈佛大學,由米哈伊爾·盧金(Mikhail Lukin)教授領導的一個研究小組使用金剛石色心系統也取得了類似的結果[9]。最近,用量子計算機模擬多體離散時間晶體也得以實現[10,11,12]。其中,谷歌團隊利用谷歌的懸鈴木量子處理器在鏈狀的20個超導比特中觀察到穩定的時間晶體[20]。與此同時,關于離散時間晶體的擴展理論也在蓬勃發展中,比如,基于Dicke 模型實現離散時間晶體[13],基于里德堡原子鏈實現離散時間晶體[14],拓撲離散時間晶體等[15]。
3、在光力系統中構造離散時間晶體
然后我們考慮在光腔中嵌入兩個機械振子的腔光力學模型中實現離散時間晶體的方案。腔光力學主要探究的是電磁場和機械模式之間的相互作用,作為現代物理學中一個快速發展的領域,在過去的十幾年中,它已成為探索宏觀量子力學行為和量子信息處理最有前途的平臺之一。在光腔中嵌入兩個機械振子的光力學模型可以被映射到Dicke模型,在熱力學極限下可以通過調節耦合參數來實現超輻射量子相變。我們可以通過以為周期來調節失諧和驅動振幅來改變相變的臨界點,使得系統在超輻射量子相變的兩個穩態之間切換進而實現周期為的Dicke型離散時間晶體。
基于以上原理,我們先介紹在光腔中嵌入兩個機械振子的光力學模型,兩個機械振子分別被放置于光學模的波峰和波谷處,因此只需要考慮相反的二階光力學相互作用。在考慮光力學哈密頓量的線性化近似(將光場的振幅分成一個相干(經典)部分加上一個波動: )和旋波近似下,系統的有效哈密頓量可以寫為,這里()是光學模式(兩個機械振子模式)的湮滅算符,是通過橫梁耦合的兩個機械振子之間直接相互作用強度。表示單模光腔的經典振幅,表示光腔的失諧。對于這個有效哈密頓量,總聲子數是守恒量。利用Schwinger變換 有效哈密頓量可以被完全映射到Dicke模型并且具有在變換下保持不變的對稱性。類比Dicke模型,這個對稱性的自發破缺導致了量子相變。也就是說,在熱力學極限聲子數下當光力學耦合強度大于臨界耦合強度時,對稱性自發破缺,系統的基態發生從正常態到超輻射態的二階量子相變,序參量從零變成具有一定的宏觀占據,系統的自由能從拋物線型變成雙阱勢。為了方便后面的表述,我們把系統的兩個超輻射穩態可以記成。
我們選取其中一個穩態作為初態(可以通過某一初態經過足夠長時間演化而得到)。我們固定耦合強度,同時調整失諧和驅動幅度來調節臨界耦合強度實現正常相和超輻射相的轉換,進而使得系統在兩個穩態之間不斷切換。一個精確的倍周期Floquet動力學方案可以通過如下四個步驟得到(如圖2)。其中階段1和3,系統處于正常相,由于初值的限制,序參量將在附近振蕩,我們可以選取合適的時間使其翻轉。階段2和4,系統處于超輻射相,系統逐漸演化到相應的穩態上去。如示意圖(2. b)中藍色線所示,當我們不斷重復這樣的行為時就可以在實現倍周期的離散時間晶體行為。在熱力學極限下,示意圖中黑色線表示的頻閃動力學也會無止盡的振蕩下去。并且通過數值模擬,我們發現在熱力學極限下這種方案下的離散時間晶體行為是滿足長時性以及對參數起伏有一定的魯棒性。
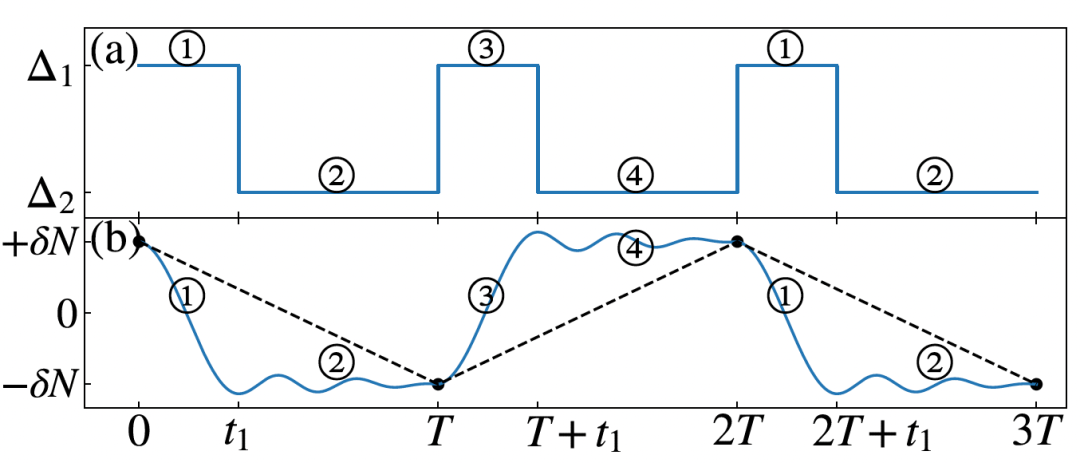
實現離散時間晶體方案示意圖。
綜上,我們簡單介紹了時間晶體的提出,離散時間晶體的概念、時間晶體的發展以及在光腔中插入兩個機械振子的光力系統模型中理論上如何產生離散時間晶體行為的方案,希望可以讓讀者對離散時間晶體有初步的了解。
參考文獻
[1] Wilczek, Frank. "Quantum time crystals." Physical review letters 109.16 (2012): 160401.
[2] Li, Tongcang, et al. "Space-time crystals of trapped ions." Physical review letters 109.16(2012): 163001.
[3] P. Bruno, Phys. Rev. Lett. 111, 070402 (2013).
[4] H. Watanabe and M. Oshikawa, Phys. Rev. Lett. 114, 251603 (2015).
[5] K. Sacha, Phys. Rev. A, 91: 033617 (2015).
[6] A. Russomanno, F. Iemini, M. Dalmonte, and R. Fazio, Phys. Rev. B 95, 214307 (2017).
[7] B. Huang, Y. H. Wu, and W. V. Liu, Phys. Rev. Lett. 120, 110603 (2018).
[8] J. Zhang, et al, Nature, 543(7644): 217-220 (2017)
[9] S. Choi, et al, Nature, 543(7644): 221-225 (2017).
[10] X. Mi, et al. Nature , 601(7894): 531-536 (2022).
[11] H. Xu, et al, arXiv, 2021. https://arxiv.org/abs/2108.00942.
[12] X. Zhang, et al. arXiv, 2021. https://arxiv.org/abs/2109.05577.
[13] Z. Gong, et al. Phys. Rev. Lett., 120: 040404 (2018).
[14] C. H. Fan, et al. Phys. Rev. A, 2020, 101: 013417(2020).
[15] K. Giergiel, et al. New Journal of Physics, 21(5): 052003 (2019).
[16] 郭啟淏、尹璋琦-時間晶體: 構想、爭議與實現.
[17] https://en.wikipedia.org/wiki/Time_crystal.
編輯:黃飛
-
晶體
+關注
關注
2文章
1367瀏覽量
35506
原文標題:光力學系統中的離散時間晶體現象
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
LabVIEW的離散時間系統的時頻域分析
離散時間信號與系統
離散時間信號與系統的詳細教程詳細概述




 什么是離散時間晶體 光力系統中構造離散時間晶體
什么是離散時間晶體 光力系統中構造離散時間晶體













評論