晶體結(jié)構(gòu)是通過(guò)原子（或離子/分子）組的周期性分布來(lái)實(shí)現(xiàn)的。理想情況下，考慮到在空間坐標(biāo)中延伸到無(wú)窮大的晶體，周期性轉(zhuǎn)化為平移不變性（或平移對(duì)稱(chēng)性）。因此，整個(gè)晶體是由稱(chēng)為晶胞的基本單元的周期性重復(fù)產(chǎn)生的，該晶胞可以包含原子/離子/分子/電子組，并且是電中性的。

平移對(duì)稱(chēng)性意味著屬于基本單元的通用點(diǎn)與通過(guò)從第一個(gè)適當(dāng)平移獲得的基本單元的點(diǎn)一一對(duì)應(yīng)。在數(shù)學(xué)上，整個(gè)結(jié)構(gòu)可以由三個(gè)線(xiàn)性獨(dú)立的向量（a 1 、 a 2 、 a 3 ）生成（因此，不共面）。更準(zhǔn)確地說(shuō)，晶格的節(jié)點(diǎn)被定位（相對(duì)于給定的笛卡爾參考Oxyz）

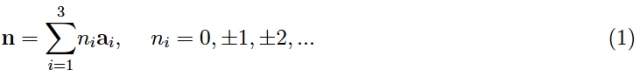
定義1：向量a 1、a 2、a 3稱(chēng)為基本平移向量，n類(lèi)型向量稱(chēng)為格向量。幾何位置稱(chēng)為布拉維格，或空間格。

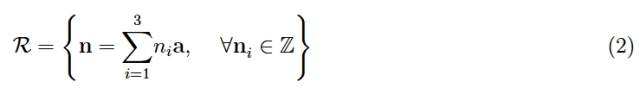
定義2：基本平移的向量標(biāo)識(shí)了一個(gè)平行六面體，稱(chēng)為原始單元。

分配格并不意味著唯一確定基本平移的向量。例如，讓我們考慮一個(gè) 2D 晶格，如圖 1 所示，我們看到可以通過(guò)幾種不同的方式選擇這些向量。

除了平移對(duì)稱(chēng)性之外，還可能存在關(guān)于某些軸的旋轉(zhuǎn)對(duì)稱(chēng)性。更準(zhǔn)確地說(shuō)，格子的通用向量n被轉(zhuǎn)換為由同一節(jié)點(diǎn)標(biāo)記的向量n ' 。對(duì)于旋轉(zhuǎn)，相對(duì)于60 °和90 °的旋轉(zhuǎn)及其整數(shù)倍數(shù)，例如用C 6 、C 9表示相應(yīng)的對(duì)稱(chēng)性。然后我們有反演 n → n ' = - n，以及相對(duì)于指定平面的鏡面反射。通過(guò)添加相同的變換 n →n ′ = n，這樣的變換集合假定代數(shù)群結(jié)構(gòu)，稱(chēng)為布拉維格的對(duì)稱(chēng)群。有 14 個(gè)對(duì)稱(chēng)群，因此有 14 個(gè)布拉維晶格，這反過(guò)來(lái)又產(chǎn)生了 230 個(gè)晶體結(jié)構(gòu)。1,2

Wigner-Seitz 細(xì)胞

如上所述，可以以幾種不同的方式選擇原始單元。通常，它遵循單細(xì)胞水平晶格對(duì)稱(chēng)性的非守恒。圖 2 顯示了一個(gè)示例，其中我們有一個(gè)具有明顯六邊形對(duì)稱(chēng)性的二維晶格。通過(guò)對(duì)原始單元的指定選擇，我們看到這種對(duì)稱(chēng)性不是局部守恒的，因?yàn)閱挝粏卧槐憩F(xiàn)出這種對(duì)稱(chēng)性。

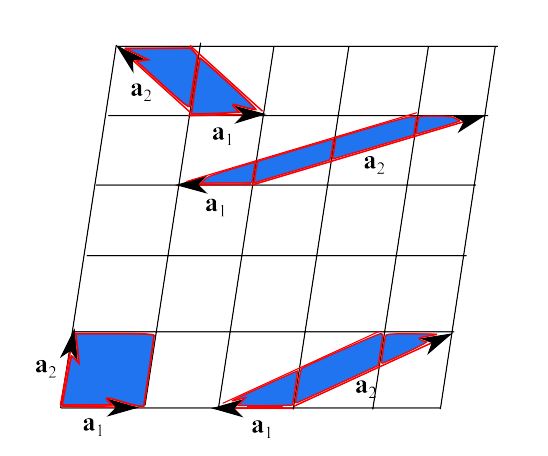
圖 1：二維晶格。可以以幾種不同的方式選擇基本翻譯的向量。由此可見(jiàn)，原始細(xì)胞不是唯一的。

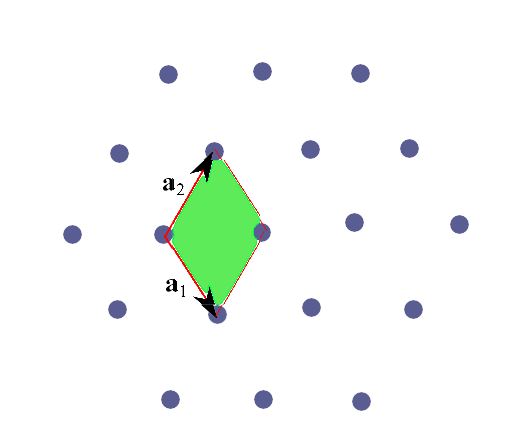
圖 2：由基本平移 a 1 、 a 2的向量標(biāo)識(shí)的原始單元不具有晶格的對(duì)稱(chēng)性。

但是，有一個(gè)過(guò)程可以構(gòu)建與晶格具有相同對(duì)稱(chēng)性的原始單元：

從分配的節(jié)點(diǎn)開(kāi)始，繪制將節(jié)點(diǎn)連接到其鄰居的線(xiàn)段。

從每一段，垂線(xiàn)被繪制到中點(diǎn)。

正如我們?cè)趫D 3 中看到的，獲得的原始單元具有六邊形對(duì)稱(chēng)性。

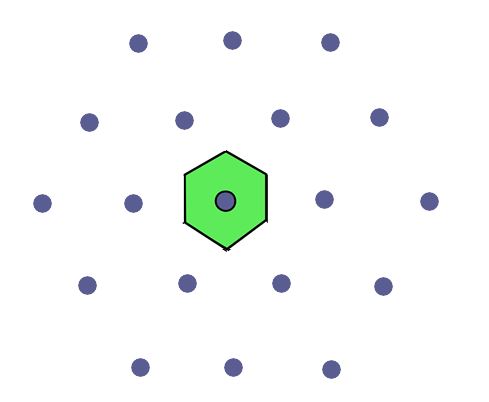
圖 3：用上述過(guò)程識(shí)別的原始細(xì)胞表現(xiàn)出與晶格相同的對(duì)稱(chēng)性。

上述過(guò)程具有普遍有效性，因此，它在局部級(jí)別再現(xiàn)了網(wǎng)狀對(duì)稱(chēng)性，即單個(gè)原始細(xì)胞的網(wǎng)狀對(duì)稱(chēng)性，稱(chēng)為Wigner-Seitz細(xì)胞。

六角點(diǎn)陣和立方點(diǎn)陣

在這項(xiàng)工作中，我們對(duì)立方晶格和六方晶格感興趣。第一種分別表示為簡(jiǎn)單立方晶格 (sc)、體心晶格 (bcc)和面心晶格 (fcc)（圖 4）。

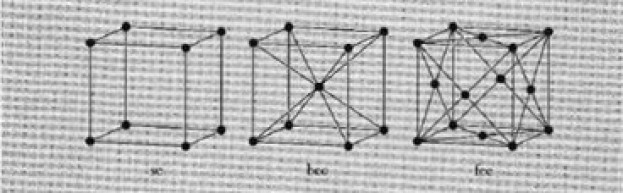
圖 4：立方晶格的配置（來(lái)源：固體物理學(xué)簡(jiǎn)介2）

六邊形晶格是上述晶格的 3D 擴(kuò)展。如圖 5 所示。

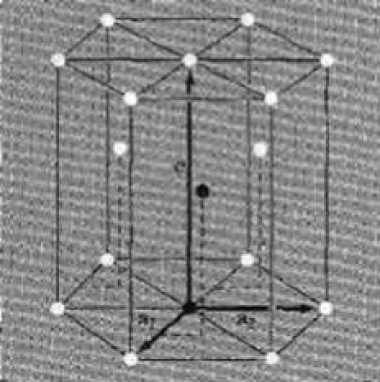
圖 5：六邊形圖案（來(lái)源：Solid State Physics 2簡(jiǎn)介）

碳化硅和氮化鎵

在前幾期中，我們研究了 Bravais 晶格的更簡(jiǎn)單配置；我們現(xiàn)在必須添加“磚塊”或構(gòu)成物質(zhì)（原子/離子/分子）。一般來(lái)說(shuō)，有分子或晶體類(lèi)型的復(fù)合系統(tǒng)，由原子等基本單元組成。讓我們以鈉原子（Na）和氯原子（Cl）為例。第一個(gè)的原子序數(shù)為Z = 11 ，而第二個(gè)的原子序數(shù)為Z = 17。如果我們“接近”這兩個(gè)原子，鈉會(huì)失去一個(gè)電子，變成正離子 Na +，失去的電子被氯獲得, 變成負(fù)離子 Cl –。這些離子通過(guò)靜電力（離子鍵）。結(jié)果是分子的形成。這種類(lèi)型的鍵沒(méi)有飽和度，因?yàn)樗梢詡鞑ィo電）到其他離子，從而產(chǎn)生一種特定的凝聚結(jié)構(gòu)，稱(chēng)為離子晶體。

然而，在分子晶體中，內(nèi)聚力是由范德華力引起的，范德華力作用于分子之間，例如 H 2、O 2、CO 和各種碳化合物。

我們研究的興趣是共價(jià)晶體：由于價(jià)電子，與相鄰原子建立了鍵。硅和鍺就是這種情況：

硅（Z = 14）；鍺 ( Z = 32)

兩者都有四個(gè)價(jià)電子，它們與相鄰的價(jià)電子形成鍵，如圖 6 所示，其中每對(duì)電子都處于自旋單重態(tài)（即反平行自旋）。

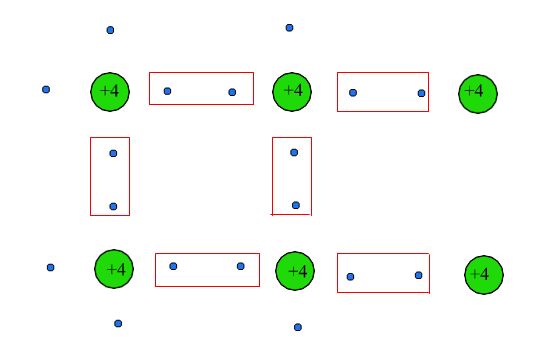
圖 6：彩色矩形代表共價(jià)鍵。

碳化硅和氮化鎵展示了類(lèi)似的配置，即共價(jià)鍵的 3D 映射。第一種在自然界中幾乎不以礦物（莫桑石）的形式存在，因此它在工業(yè)上通過(guò)以等比例的碳和硅為原料進(jìn)行合成，以獲得相同濃度的兩種化學(xué)元素的原子。

最受技術(shù)應(yīng)用關(guān)注的碳化硅晶體形式是α（α -SiC）和β（β -SiC）。Alpha 具有六邊形結(jié)構(gòu)，而 Beta 具有面心立方結(jié)構(gòu)。在文獻(xiàn)中，符號(hào) H-SiC 和 C-SiC 通常用于區(qū)分 alpha 和 beta 狀態(tài)，即分別為六方和立方對(duì)稱(chēng)。

碳化硅具有有趣的熱特性，例如低熱膨脹系數(shù)和高升華溫度。正如我們將在下一期中看到的那樣，這些特性轉(zhuǎn)化為關(guān)于電力電子設(shè)備輻射的卓越可靠性。

相比之下，GaN 在自然界中以纖鋅礦（鋅和鐵的硫化物）的形式存在，但在這種情況下，鑒于擴(kuò)散稀少，我們嘗試合成生產(chǎn)它。由于與SiC（我們將在下一期中研究的物理量）相比，它具有更高的電子遷移率，因此在射頻電子設(shè)備中發(fā)現(xiàn)了它的最佳性能。如前所述，碳化硅由于其熱特性（包括高導(dǎo)熱性，可以更好地在環(huán)境中散熱）而更適用于電力電子產(chǎn)品。

審核編輯：湯梓紅