看起來PID高大尚,先被別人唬住,后被公式唬住,由于大多數人高數一點都不會或者遺忘,所以再一看公式,簡直嚇死。
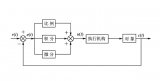
直接從網上找了PID相關公式截圖如下。

了解了很淺的原理后,結果公式看不懂,不懂含義,所以最終沒有透徹。我這里先對公式進行剖析,公式理解明白了,結合網上的一些PID講述的例子,就明白了。
先對PID這三個系數的含義進行簡單掃盲。同時也防止自己遺忘。P是比例系數,I是積分系數、D是微分系數。
下面對PID這三個系數進行詳細說明:演示PID三個參數的控制作用。
比例系數P
比例系數P是干什么用,其實如果現在你是初中生的話,你一下子就懂了,比例系數就是用在穿過(0,0)這個坐標點直線的放大倍數k,k越大,直線的斜率越大,所以是用在y = k * x中的,其中的k就是比例系數p,大家都簡稱為kp,所以就變成了y = Kp * x。
x就是當前值currentValue和目標值totalValue的差值,簡稱誤差err,則err = currentValue - totalValue。y就是執行器對應的輸出值U,所以執行器對應的輸出值U = Kp * ( currentValue - totalValue ) 。
所以,如果說是使用比例進行調節。
則當前第1次調節時執行器對應的輸出值為:
U1 = Kp * ( curentValue1 - totalValue1 )
第2次調節時執行器對應的輸出值為:
U2 = Kp * ( currentValue2 - totalValue2 )
這就是比例系數P的應用,也就是大家說的比例調節。比例調節就是根據當前的值與目標值的差值,乘以了一個Kp的系數,來得到一個輸出值,這輸出值直接影響了下次當前值的變化。如果只有比例調節的話,系統會震蕩的比較厲害。比如你的汽車現在運行的速度是60km/h,現在你想通過你的執行器去控制這個汽車達到恒定的50km/h,如果你只用kp進行比例調節話。U = Kp * ( 60 - 50 ),假設Kp取值為1,此時得到U執行器的輸出值是10,結果當你執行器輸出后,發現汽車一下變成了35Km/h,此時U2 = Kp * (35 - 50),此時得到U執行器的輸出值是-15,結果當你執行器輸出后,發現汽車變成了55Km/h,由于慣性和不可預知的誤差因素,你的汽車始終無法達到恒定的50km/h。始終在晃動,相信如果你在車上,你一定吐的很厲害。所以光有比例系數進行調節,在有些場合是沒有辦法將系統調穩定的。所以可以為了減緩震蕩的厲害,則會結合使用比例P和微分D。
微分系數D
微分,實際上是對誤差進行微分。加入誤差1是err(1)。誤差2是err(2)。則誤差err的微分是 (err2 - err1)。乘上微分系數D,大家叫做KD,則當執行器第1次調節后有了第1次的誤差,第2次調節后有了第2次的誤差,則結合P系數。就有了PD結合,根據每次調節時,誤差的值的經驗推算,你就能選取出D的系數。假如誤差是越來越小的,那么微分后肯定是一個負值。負值在乘以了一個D系數 加上了比例調節的值后肯定值要比單純使用比例調節的值要小,所以就啟到了阻尼的作用。有了阻尼的作用就會使得系統區域穩定。
PD結合的公式經過上面的分析后為:
U(t) = Kp * err(t) + Kd * derr(t)/dt
積分系數I
積分,實際上是對誤差的積分,也就是誤差的無限和。如何理解積分系數I,這里引用網上的例子
以熱水為例。假如有個人把我們的加熱裝置帶到了非常冷的地方,開始燒水了。需要燒到50℃。
在P的作用下,水溫慢慢升高。直到升高到45℃時,他發現了一個不好的事情:天氣太冷,水散熱的速度,和P控制的加熱的速度相等了。
這可怎么辦?
P兄這樣想:我和目標已經很近了,只需要輕輕加熱就可以了。
D兄這樣想:加熱和散熱相等,溫度沒有波動,我好像不用調整什么。
于是,水溫永遠地停留在45℃,永遠到不了50℃。
根據常識,我們知道,應該進一步增加加熱的功率。可是增加多少該如何計算呢?
前輩科學家們想到的方法是真的巧妙。
設置一個積分量。只要偏差存在,就不斷地對偏差進行積分(累加),并反應在調節力度上。
這樣一來,即使45℃和50℃相差不太大,但是隨著時間的推移,只要沒達到目標溫度,這個積分量就不斷增加。系統就會慢慢意識到:還沒有到達目標溫度,該增加功率啦!
到了目標溫度后,假設溫度沒有波動,積分值就不會再變動。這時,加熱功率仍然等于散熱功率。但是,溫度是穩穩的50℃。
kI的值越大,積分時乘的系數就越大,積分效果越明顯。
所以,I的作用就是,減小靜態情況下的誤差,讓受控物理量盡可能接近目標值。
I在使用時還有個問題:需要設定積分限制。防止在剛開始加熱時,就把積分量積得太大,難以控制。最后推薦下相關文章:PID到底是個啥?講個故事告訴你。
原文標題:PID算法終于弄明白了,沒有公式那么嚇人
文章出處:【微信公眾號:STM32嵌入式開發】歡迎添加關注!文章轉載請注明出處。
審核編輯:湯梓紅
-
PID
+關注
關注
35文章
1473瀏覽量
85729 -
參數
+關注
關注
11文章
1859瀏覽量
32388
原文標題:PID算法終于弄明白了,沒有公式那么嚇人
文章出處:【微信號:c-stm32,微信公眾號:STM32嵌入式開發】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 PID相關公式介紹及三個參數的控制作用
PID相關公式介紹及三個參數的控制作用













評論