讀完本文，可以去力扣解決如下題目：

743. 網絡延遲時間（中等）

1514. 概率最大的路徑（中等）

1631. 最小體力消耗路徑（中等）

其實，很多算法的底層原理異常簡單，無非就是一步一步延伸，變得看起來好像特別復雜，特別牛逼。

但如果你看過歷史文章，應該可以對算法形成自己的理解，就會發現很多算法都是換湯不換藥，毫無新意，非常枯燥。

比如，我們說二叉樹非常重要，你把這個結構掌握了，就會發現 動態規劃，分治算法，回溯（DFS）算法，BFS 算法框架，Union-Find 并查集算法，二叉堆實現優先級隊列 就是把二叉樹翻來覆去的運用。

那么本文又要告訴你，Dijkstra 算法（一般音譯成迪杰斯特拉算法）無非就是一個 BFS 算法的加強版，它們都是從二叉樹的層序遍歷衍生出來的。

這也是為什么我在 學習數據結構和算法的框架思維 中這么強調二叉樹的原因。

下面我們由淺入深，從二叉樹的層序遍歷聊到 Dijkstra 算法，給出 Dijkstra 算法的代碼框架，順手秒殺幾道運用 Dijkstra 算法的題目。

圖的抽象

前文 圖論第一期：遍歷基礎 說過「圖」這種數據結構的基本實現，圖中的節點一般就抽象成一個數字（索引），圖的具體實現一般是「鄰接矩陣」或者「鄰接表」。

比如上圖這幅圖用鄰接表和鄰接矩陣的存儲方式如下：

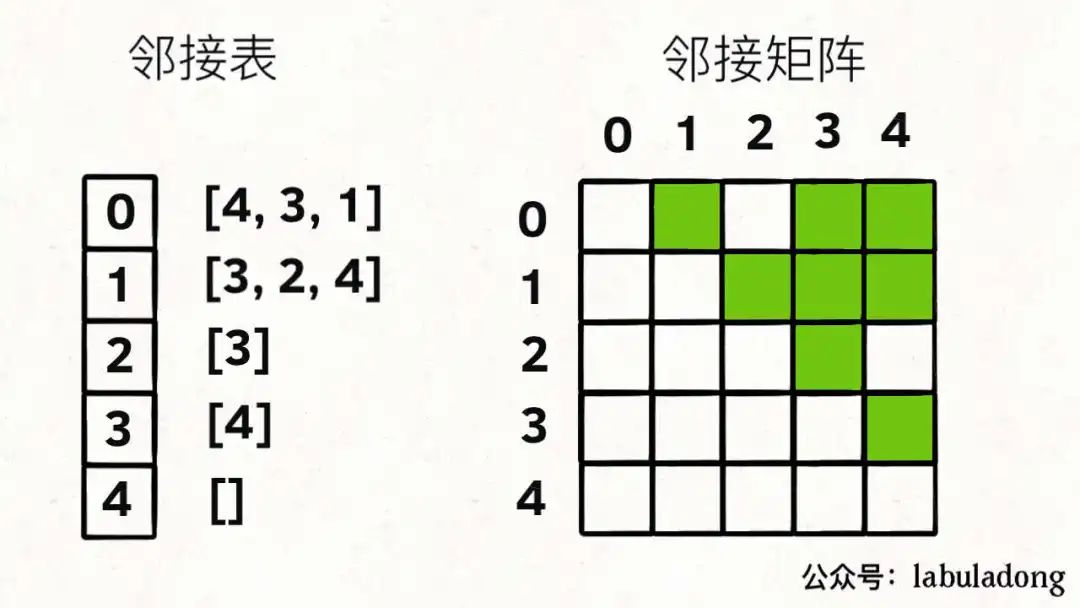
前文 圖論第二期：拓撲排序 告訴你，我們用鄰接表的場景更多，結合上圖，一幅圖可以用如下 Java 代碼表示：

// graph［s］ 存儲節點 s 指向的節點（出度）

List《Integer》［］ graph;

如果你想把一個問題抽象成「圖」的問題，那么首先要實現一個 APIadj：

// 輸入節點 s 返回 s 的相鄰節點List《Integer》 adj（int s）;

類似多叉樹節點中的children字段記錄當前節點的所有子節點，adj（s）就是計算一個節點s的相鄰節點。

比如上面說的用鄰接表表示「圖」的方式，adj函數就可以這樣表示：

List《Integer》［］ graph;

// 輸入節點 s，返回 s 的相鄰節點List《Integer》 adj（int s） {

return graph［s］;

}

當然，對于「加權圖」，我們需要知道兩個節點之間的邊權重是多少，所以還可以抽象出一個weight方法：

// 返回節點 from 到節點 to 之間的邊的權重int weight（int from， int to）;

這個weight方法可以根據實際情況而定，因為不同的算法題，題目給的「權重」含義可能不一樣，我們存儲權重的方式也不一樣。

有了上述基礎知識，就可以搞定 Dijkstra 算法了，下面我給你從二叉樹的層序遍歷開始推演出 Dijkstra 算法的實現。

二叉樹層級遍歷和 BFS 算法

我們之前說過二叉樹的層級遍歷框架：

// 輸入一棵二叉樹的根節點，層序遍歷這棵二叉樹void levelTraverse（TreeNode root） {

if （root == null） return 0;

Queue《TreeNode》 q = new LinkedList《》（）;

q.offer（root）;

int depth = 1;

// 從上到下遍歷二叉樹的每一層

while （！q.isEmpty（）） {

int sz = q.size（）;

// 從左到右遍歷每一層的每個節點

for （int i = 0; i 《 sz; i++） {

TreeNode cur = q.poll（）;

printf（“節點 %s 在第 %s 層”， cur， depth）;

// 將下一層節點放入隊列

if （cur.left ！= null） {

q.offer（cur.left）;

}

if （cur.right ！= null） {

q.offer（cur.right）;

}

}

depth++;

}

}

我們先來思考一個問題，注意二叉樹的層級遍歷while循環里面還套了個for循環，為什么要這樣？

while循環和for循環的配合正是這個遍歷框架設計的巧妙之處

while循環控制一層一層往下走，for循環利用sz變量控制從左到右遍歷每一層二叉樹節點。

注意我們代碼框架中的depth變量，其實就記錄了當前遍歷到的層數。換句話說，每當我們遍歷到一個節點cur，都知道這個節點屬于第幾層。

算法題經常會問二叉樹的最大深度呀，最小深度呀，層序遍歷結果呀，等等問題，所以記錄下來這個深度depth是有必要的。

基于二叉樹的遍歷框架，我們又可以擴展出多叉樹的層序遍歷框架：

// 輸入一棵多叉樹的根節點，層序遍歷這棵多叉樹void levelTraverse（TreeNode root） {

if （root == null） return 0;

Queue《TreeNode》 q = new LinkedList《》（）;

q.offer（root）;

int depth = 1;

// 從上到下遍歷多叉樹的每一層

while （！q.isEmpty（）） {

int sz = q.size（）;

// 從左到右遍歷每一層的每個節點

for （int i = 0; i 《 sz; i++） {

TreeNode cur = q.poll（）;

printf（“節點 %s 在第 %s 層”， cur， depth）;

// 將下一層節點放入隊列

for （TreeNode child ： root.children） {

q.offer（child）;

}

}

depth++;

}

}

基于多叉樹的遍歷框架，我們又可以擴展出 BFS（廣度優先搜索）的算法框架：

// 輸入起點，進行 BFS 搜索int BFS（Node start） {

Queue《Node》 q; // 核心數據結構

Set《Node》 visited; // 避免走回頭路

q.offer（start）; // 將起點加入隊列

visited.add（start）;

int step = 0; // 記錄搜索的步數

while （q not empty） {

int sz = q.size（）;

/* 將當前隊列中的所有節點向四周擴散一步 */

for （int i = 0; i 《 sz; i++） {

Node cur = q.poll（）;

printf（“從 %s 到 %s 的最短距離是 %s”， start， cur， step）;

/* 將 cur 的相鄰節點加入隊列 */

for （Node x ： cur.adj（）） {

if （x not in visited） {

q.offer（x）;

visited.add（x）;

}

}

}

step++;

}

}

如果對 BFS 算法不熟悉，可以看前文 BFS 算法框架，這里只是為了讓你做個對比，所謂 BFS 算法，就是把算法問題抽象成一幅「無權圖」，然后繼續玩二叉樹層級遍歷那一套罷了。

注意，我們的 BFS 算法框架也是while循環嵌套for循環的形式，也用了一個step變量記錄for循環執行的次數，無非就是多用了一個visited集合記錄走過的節點，防止走回頭路罷了。

為什么這樣呢？

所謂「無權圖」，與其說每條「邊」沒有權重，不如說每條「邊」的權重都是 1，從起點start到任意一個節點之間的路徑權重就是它們之間「邊」的條數，那可不就是step變量記錄的值么？

再加上 BFS 算法利用for循環一層一層向外擴散的邏輯和visited集合防止走回頭路的邏輯，當你每次從隊列中拿出節點cur的時候，從start到cur的最短權重就是step記錄的步數。

但是，到了「加權圖」的場景，事情就沒有這么簡單了，因為你不能默認每條邊的「權重」都是 1 了，這個權重可以是任意正數（Dijkstra 算法要求不能存在負權重邊），比如下圖的例子：

如果沿用 BFS 算法中的step變量記錄「步數」，顯然紅色路徑一步就可以走到終點，但是這一步的權重很大；正確的最小權重路徑應該是綠色的路徑，雖然需要走很多步，但是路徑權重依然很小。

其實 Dijkstra 和 BFS 算法差不多，不過在講解 Dijkstra 算法框架之前，我們首先需要對之前的框架進行如下改造：

想辦法去掉while循環里面的for循環。

為什么？有了剛才的鋪墊，這個不難理解，剛才說for循環是干什么用的來著？

是為了讓二叉樹一層一層往下遍歷，讓 BFS 算法一步一步向外擴散，因為這個層數depth，或者這個步數step，在之前的場景中有用。

但現在我們想解決「加權圖」中的最短路徑問題，「步數」已經沒有參考意義了，「路徑的權重之和」才有意義，所以這個for循環可以被去掉。

怎么去掉？就拿二叉樹的層級遍歷來說，其實你可以直接去掉for循環相關的代碼：

// 輸入一棵二叉樹的根節點，遍歷這棵二叉樹所有節點void levelTraverse（TreeNode root） {

if （root == null） return 0;

Queue《TreeNode》 q = new LinkedList《》（）;

q.offer（root）;

// 遍歷二叉樹的每一個節點

while （！q.isEmpty（）） {

TreeNode cur = q.poll（）;

printf（“我不知道節點 %s 在第幾層”， cur）;

// 將子節點放入隊列

if （cur.left ！= null） {

q.offer（cur.left）;

}

if （cur.right ！= null） {

q.offer（cur.right）;

}

}

}

但問題是，沒有for循環，你也沒辦法維護depth變量了。

如果你想同時維護depth變量，讓每個節點cur知道自己在第幾層，可以想其他辦法，比如新建一個State類，記錄每個節點所在的層數：

class State {

// 記錄 node 節點的深度

int depth;

TreeNode node;

State（TreeNode node， int depth） {

this.depth = depth;

this.node = node;

}

}

// 輸入一棵二叉樹的根節點，遍歷這棵二叉樹所有節點void levelTraverse（TreeNode root） {

if （root == null） return 0;

Queue《State》 q = new LinkedList《》（）;

q.offer（new State（root， 1））;

// 遍歷二叉樹的每一個節點

while （！q.isEmpty（）） {

State cur = q.poll（）;

TreeNode cur_node = cur.node;

int cur_depth = cur.depth;

printf（“節點 %s 在第 %s 層”， cur_node， cur_depth）;

// 將子節點放入隊列

if （cur_node.left ！= null） {

q.offer（new State（cur_node.left， cur_depth + 1））;

}

if （cur_node.right ！= null） {

q.offer（new State（cur_node.right， cur_depth + 1））;

}

}

}

這樣，我們就可以不使用for循環也確切地知道每個二叉樹節點的深度了。

如果你能夠理解上面這段代碼，我們就可以來看 Dijkstra 算法的代碼框架了。

Dijkstra 算法框架

首先，我們先看一下 Dijkstra 算法的簽名：

// 輸入一幅圖和一個起點 start，計算 start 到其他節點的最短距離int［］ dijkstra（int start， List《Integer》［］ graph）;

輸入是一幅圖graph和一個起點start，返回是一個記錄最短路徑權重的數組。

比方說，輸入起點start = 3，函數返回一個int［］數組，假設賦值給distTo變量，那么從起點3到節點6的最短路徑權重的值就是distTo［6］。

是的，標準的 Dijkstra 算法會把從起點start到所有其他節點的最短路徑都算出來。

當然，如果你的需求只是計算從起點start到某一個終點end的最短路徑，那么在標準 Dijkstra 算法上稍作修改就可以更高效地完成這個需求，這個我們后面再說。

其次，我們也需要一個State類來輔助算法的運行：

class State {

// 圖節點的 id

int id;

// 從 start 節點到當前節點的距離

int distFromStart;

State（int id， int distFromStart） {

this.id = id;

this.distFromStart = distFromStart;

}

}

類似剛才二叉樹的層序遍歷，我們也需要用State類記錄一些額外信息，也就是使用distFromStart變量記錄從起點start到當前這個節點的距離。

剛才說普通 BFS 算法中，根據 BFS 的邏輯和無權圖的特點，第一次遇到某個節點所走的步數就是最短距離，所以用一個visited數組防止走回頭路，每個節點只會經過一次。

加權圖中的 Dijkstra 算法和無權圖中的普通 BFS 算法不同，在 Dijkstra 算法中，你第一次經過某個節點時的路徑權重，不見得就是最小的，所以對于同一個節點，我們可能會經過多次，而且每次的distFromStart可能都不一樣，比如下圖：

我會經過節點5三次，每次的distFromStart值都不一樣，那我取distFromStart最小的那次，不就是從起點start到節點5的最短路徑權重了么？

好了，明白上面的幾點，我們可以來看看 Dijkstra 算法的代碼模板。

其實，Dijkstra 可以理解成一個帶 dp table（或者說備忘錄）的 BFS 算法，偽碼如下：

// 返回節點 from 到節點 to 之間的邊的權重int weight（int from， int to）;

// 輸入節點 s 返回 s 的相鄰節點List《Integer》 adj（int s）;

// 輸入一幅圖和一個起點 start，計算 start 到其他節點的最短距離int［］ dijkstra（int start， List《Integer》［］ graph） {

// 圖中節點的個數

int V = graph.length;

// 記錄最短路徑的權重，你可以理解為 dp table

// 定義：distTo［i］ 的值就是節點 start 到達節點 i 的最短路徑權重

int［］ distTo = new int［V］;

// 求最小值，所以 dp table 初始化為正無窮

Arrays.fill（distTo， Integer.MAX_VALUE）;

// base case，start 到 start 的最短距離就是 0

distTo［start］ = 0;

// 優先級隊列，distFromStart 較小的排在前面

Queue《State》 pq = new PriorityQueue《》（（a， b） -》 {

return a.distFromStart - b.distFromStart;

}）;

// 從起點 start 開始進行 BFS

pq.offer（new State（start， 0））;

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curNodeID = curState.id;

int curDistFromStart = curState.distFromStart;

if （curDistFromStart 》 distTo［curNodeID］） {

// 已經有一條更短的路徑到達 curNode 節點了

continue;

}

// 將 curNode 的相鄰節點裝入隊列

for （int nextNodeID ： adj（curNodeID）） {

// 看看從 curNode 達到 nextNode 的距離是否會更短

int distToNextNode = distTo［curNodeID］ + weight（curNodeID， nextNodeID）;

if （distTo［nextNodeID］ 》 distToNextNode） {

// 更新 dp table

distTo［nextNodeID］ = distToNextNode;

// 將這個節點以及距離放入隊列

pq.offer（new State（nextNodeID， distToNextNode））;

}

}

}

return distTo;

}

對比普通的 BFS 算法，你可能會有以下疑問：

1、沒有visited集合記錄已訪問的節點，所以一個節點會被訪問多次，會被多次加入隊列，那會不會導致隊列永遠不為空，造成死循環？

2、為什么用優先級隊列PriorityQueue而不是LinkedList實現的普通隊列？為什么要按照distFromStart的值來排序？

3、如果我只想計算起點start到某一個終點end的最短路徑，是否可以修改算法，提升一些效率？

我們先回答第一個問題，為什么這個算法不用visited集合也不會死循環。

對于這類問題，我教你一個思考方法：

循環結束的條件是隊列為空，那么你就要注意看什么時候往隊列里放元素（調用offer）方法，再注意看什么時候從隊列往外拿元素（調用poll方法）。

while循環每執行一次，都會往外拿一個元素，但想往隊列里放元素，可就有很多限制了，必須滿足下面這個條件：

// 看看從 curNode 達到 nextNode 的距離是否會更短if （distTo［nextNodeID］ 》 distToNextNode） {

// 更新 dp table

distTo［nextNodeID］ = distToNextNode;

pq.offer（new State（nextNodeID， distToNextNode））;

}

這也是為什么我說distTo數組可以理解成我們熟悉的 dp table，因為這個算法邏輯就是在不斷的最小化distTo數組中的元素：

如果你能讓到達nextNodeID的距離更短，那就更新distTo［nextNodeID］的值，讓你入隊，否則的話對不起，不讓入隊。

因為兩個節點之間的最短距離（路徑權重）肯定是一個確定的值，不可能無限減小下去，所以隊列一定會空，隊列空了之后，distTo數組中記錄的就是從start到其他節點的最短距離。

接下來解答第二個問題，為什么要用PriorityQueue而不是LinkedList實現的普通隊列？

如果你非要用普通隊列，其實也沒問題的，你可以直接把PriorityQueue改成LinkedList，也能得到正確答案，但是效率會低很多。

Dijkstra 算法使用優先級隊列，主要是為了效率上的優化，類似一種貪心算法的思路。

為什么說是一種貪心思路呢，比如說下面這種情況，你想計算從起點start到終點end的最短路徑權重：

你下一步想遍歷那個節點？就當前的情況來看，你覺得哪條路徑更有「潛力」成為最短路徑中的一部分？

從目前的情況來看，顯然橙色路徑的可能性更大嘛，所以我們希望節點2排在隊列靠前的位置，優先被拿出來向后遍歷。

所以我們使用PriorityQueue作為隊列，讓distFromStart的值較小的節點排在前面，這就類似我們之前講 貪心算法 說到的貪心思路，可以很大程度上優化算法的效率。

大家應該聽過 Bellman-Ford 算法，這個算法是一種更通用的最短路徑算法，因為它可以處理帶有負權重邊的圖，Bellman-Ford 算法邏輯和 Dijkstra 算法非常類似，用到的就是普通隊列，本文就提一句，后面有空再具體寫。

接下來說第三個問題，如果只關心起點start到某一個終點end的最短路徑，是否可以修改代碼提升算法效率。

肯定可以的，因為我們標準 Dijkstra 算法會算出start到所有其他節點的最短路徑，你只想計算到end的最短路徑，相當于減少計算量，當然可以提升效率。

需要在代碼中做的修改也非常少，只要改改函數簽名，再加個 if 判斷就行了：

// 輸入起點 start 和終點 end，計算起點到終點的最短距離int dijkstra（int start， int end， List《Integer》［］ graph） {

// 。..

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curNodeID = curState.id;

int curDistFromStart = curState.distFromStart;

// 在這里加一個判斷就行了，其他代碼不用改

if （curNodeID == end） {

return curDistFromStart;

}

if （curDistFromStart 》 distTo［curNodeID］） {

continue;

}

// 。..

}

// 如果運行到這里，說明從 start 無法走到 end

return Integer.MAX_VALUE;

}

因為優先級隊列自動排序的性質，每次從隊列里面拿出來的都是distFromStart值最小的，所以當你從隊頭拿出一個節點，如果發現這個節點就是終點end，那么distFromStart對應的值就是從start到end的最短距離。

這個算法較之前的實現提前 return 了，所以效率有一定的提高。

時間復雜度分析

Dijkstra 算法的時間復雜度是多少？你去網上查，可能會告訴你是O（ElogV），其中E代表圖中邊的條數，V代表圖中節點的個數。

因為理想情況下優先級隊列中最多裝V個節點，對優先級隊列的操作次數和E成正比，所以整體的時間復雜度就是O（ElogV）。

不過這是理想情況，Dijkstra 算法的代碼實現有很多版本，不同編程語言或者不同數據結構 API 都會導致算法的時間復雜度發生一些改變。

比如本文實現的 Dijkstra 算法，使用了 Java 的PriorityQueue這個數據結構，這個容器類底層使用二叉堆實現，但沒有提供通過索引操作隊列中元素的 API，所以隊列中會有重復的節點，最多可能有E個節點存在隊列中。

所以本文實現的 Dijkstra 算法復雜度并不是理想情況下的O（ElogV），而是O（ElogE），可能會略大一些，因為圖中邊的條數一般是大于節點的個數的。

不過就對數函數來說，就算真數大一些，對數函數的結果也大不了多少，所以這個算法實現的實際運行效率也是很高的，以上只是理論層面的時間復雜度分析，供大家參考。

秒殺三道題目

以上說了 Dijkstra 算法的框架，下面我們套用這個框架做幾道題，實踐出真知。

第一題是力扣第 743 題「網絡延遲時間」，題目如下：

函數簽名如下：

// times 記錄邊和權重，n 為節點個數（從 1 開始），k 為起點// 計算從 k 發出的信號至少需要多久傳遍整幅圖int networkDelayTime（int［］［］ times， int n， int k）

讓你求所有節點都收到信號的時間，你把所謂的傳遞時間看做距離，實際上就是問你「從節點k到其他所有節點的最短路徑中，最長的那條最短路徑距離是多少」，說白了就是讓你算從節點k出發到其他所有節點的最短路徑，就是標準的 Dijkstra 算法。

在用 Dijkstra 之前，別忘了要滿足一些條件，加權有向圖，沒有負權重邊，OK，可以用 Dijkstra 算法計算最短路徑。

根據我們之前 Dijkstra 算法的框架，我們可以寫出下面代碼：

public int networkDelayTime（int［］［］ times， int n， int k） {

// 節點編號是從 1 開始的，所以要一個大小為 n + 1 的鄰接表

List《int［］》［］ graph = new LinkedList［n + 1］;

for （int i = 1; i 《= n; i++） {

graph［i］ = new LinkedList《》（）;

}

// 構造圖

for （int［］ edge ： times） {

int from = edge［0］;

int to = edge［1］;

int weight = edge［2］;

// from -》 List《（to， weight）》

// 鄰接表存儲圖結構，同時存儲權重信息

graph［from］.add（new int［］{to， weight}）;

}

// 啟動 dijkstra 算法計算以節點 k 為起點到其他節點的最短路徑

int［］ distTo = dijkstra（k， graph）;

// 找到最長的那一條最短路徑

int res = 0;

for （int i = 1; i 《 distTo.length; i++） {

if （distTo［i］ == Integer.MAX_VALUE） {

// 有節點不可達，返回 -1

return -1;

}

res = Math.max（res， distTo［i］）;

}

return res;

}

// 輸入一個起點 start，計算從 start 到其他節點的最短距離int［］ dijkstra（int start， List《int［］》［］ graph） {}

上述代碼首先利用題目輸入的數據轉化成鄰接表表示一幅圖，接下來我們可以直接套用 Dijkstra 算法的框架：

class State {

// 圖節點的 id

int id;

// 從 start 節點到當前節點的距離

int distFromStart;

State（int id， int distFromStart） {

this.id = id;

this.distFromStart = distFromStart;

}

}

// 輸入一個起點 start，計算從 start 到其他節點的最短距離int［］ dijkstra（int start， List《int［］》［］ graph） {

// 定義：distTo［i］ 的值就是起點 start 到達節點 i 的最短路徑權重

int［］ distTo = new int［graph.length］;

Arrays.fill（distTo， Integer.MAX_VALUE）;

// base case，start 到 start 的最短距離就是 0

distTo［start］ = 0;

// 優先級隊列，distFromStart 較小的排在前面

Queue《State》 pq = new PriorityQueue《》（（a， b） -》 {

return a.distFromStart - b.distFromStart;

}）;

// 從起點 start 開始進行 BFS

pq.offer（new State（start， 0））;

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curNodeID = curState.id;

int curDistFromStart = curState.distFromStart;

if （curDistFromStart 》 distTo［curNodeID］） {

continue;

}

// 將 curNode 的相鄰節點裝入隊列

for （int［］ neighbor ： graph［curNodeID］） {

int nextNodeID = neighbor［0］;

int distToNextNode = distTo［curNodeID］ + neighbor［1］;

// 更新 dp table

if （distTo［nextNodeID］ 》 distToNextNode） {

distTo［nextNodeID］ = distToNextNode;

pq.offer（new State（nextNodeID， distToNextNode））;

}

}

}

return distTo;

}

你對比之前說的代碼框架，只要稍稍修改，就可以把這道題目解決了。

感覺這道題完全沒有難度，下面我們再看一道題目，力扣第 1631 題「最小體力消耗路徑」：

函數簽名如下：

// 輸入一個二維矩陣，計算從左上角到右下角的最小體力消耗int minimumEffortPath（int［］［］ heights）;

我們常見的二維矩陣題目，如果讓你從左上角走到右下角，比較簡單的題一般都會限制你只能向右或向下走，但這道題可沒有限制哦，你可以上下左右隨便走，只要路徑的「體力消耗」最小就行。

如果你把二維數組中每個（x， y）坐標看做一個節點，它的上下左右坐標就是相鄰節點，它對應的值和相鄰坐標對應的值之差的絕對值就是題目說的「體力消耗」，你就可以理解為邊的權重。

這樣一想，是不是就在讓你以左上角坐標為起點，以右下角坐標為終點，計算起點到終點的最短路徑？Dijkstra 算法是不是可以做到？

// 輸入起點 start 和終點 end，計算起點到終點的最短距離int dijkstra（int start， int end， List《Integer》［］ graph）

只不過，這道題中評判一條路徑是長還是短的標準不再是路徑經過的權重總和，而是路徑經過的權重最大值。

明白這一點，再想一下使用 Dijkstra 算法的前提，加權有向圖，沒有負權重邊，求最短路徑，OK，可以使用，咱們來套框架。

二維矩陣抽象成圖，我們先實現一下圖的adj方法，之后的主要邏輯會清晰一些：

// 方向數組，上下左右的坐標偏移量int［］［］ dirs = new int［］［］{{0，1}， {1，0}， {0，-1}， {-1，0}};

// 返回坐標 （x， y） 的上下左右相鄰坐標

List《int［］》 adj（int［］［］ matrix， int x， int y） {

int m = matrix.length， n = matrix［0］.length;

// 存儲相鄰節點

List《int［］》 neighbors = new ArrayList《》（）;

for （int［］ dir ： dirs） {

int nx = x + dir［0］;

int ny = y + dir［1］;

if （nx 》= m || nx 《 0 || ny 》= n || ny 《 0） {

// 索引越界

continue;

}

neighbors.add（new int［］{nx， ny}）;

}

return neighbors;

}

類似的，我們現在認為一個二維坐標（x， y）是圖中的一個節點，所以這個State類也需要修改一下：

class State {

// 矩陣中的一個位置

int x， y;

// 從起點 （0， 0） 到當前位置的最小體力消耗（距離）

int effortFromStart;

State（int x， int y， int effortFromStart） {

this.x = x;

this.y = y;

this.effortFromStart = effortFromStart;

}

}

接下來，就可以套用 Dijkstra 算法的代碼模板了：

// Dijkstra 算法，計算 （0， 0） 到 （m - 1， n - 1） 的最小體力消耗int minimumEffortPath（int［］［］ heights） {

int m = heights.length， n = heights［0］.length;

// 定義：從 （0， 0） 到 （i， j） 的最小體力消耗是 effortTo［i］［j］

int［］［］ effortTo = new int［m］［n］;

// dp table 初始化為正無窮

for （int i = 0; i 《 m; i++） {

Arrays.fill（effortTo［i］， Integer.MAX_VALUE）;

}

// base case，起點到起點的最小消耗就是 0

effortTo［0］［0］ = 0;

// 優先級隊列，effortFromStart 較小的排在前面

Queue《State》 pq = new PriorityQueue《》（（a， b） -》 {

return a.effortFromStart - b.effortFromStart;

}）;

// 從起點 （0， 0） 開始進行 BFS

pq.offer（new State（0， 0， 0））;

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curX = curState.x;

int curY = curState.y;

int curEffortFromStart = curState.effortFromStart;

// 到達終點提前結束

if （curX == m - 1 && curY == n - 1） {

return curEffortFromStart;

}

if （curEffortFromStart 》 effortTo［curX］［curY］） {

continue;

}

// 將 （curX， curY） 的相鄰坐標裝入隊列

for （int［］ neighbor ： adj（heights， curX， curY）） {

int nextX = neighbor［0］;

int nextY = neighbor［1］;

// 計算從 （curX， curY） 達到 （nextX， nextY） 的消耗

int effortToNextNode = Math.max（

effortTo［curX］［curY］，

Math.abs（heights［curX］［curY］ - heights［nextX］［nextY］）

）;

// 更新 dp table

if （effortTo［nextX］［nextY］ 》 effortToNextNode） {

effortTo［nextX］［nextY］ = effortToNextNode;

pq.offer（new State（nextX， nextY， effortToNextNode））;

}

}

}

// 正常情況不會達到這個 return

return -1;

}

你看，稍微改一改代碼模板，這道題就解決了。

最后看一道題吧，力扣第 1514 題「概率最大的路徑」，看下題目：

函數簽名如下：

// 輸入一幅無向圖，邊上的權重代表概率，返回從 start 到達 end 最大的概率double maxProbability（int n， int［］［］ edges， double［］ succProb， int start， int end）

我說這題一看就是 Dijkstra 算法，但聰明的你肯定會反駁我：

1、這題給的是無向圖，也可以用 Dijkstra 算法嗎？

2、更重要的是，Dijkstra 算法計算的是最短路徑，計算的是最小值，這題讓你計算最大概率是一個最大值，怎么可能用 Dijkstra 算法呢？

問得好！

首先關于有向圖和無向圖，前文 圖算法基礎 說過，無向圖本質上可以認為是「雙向圖」，從而轉化成有向圖。

重點說說最大值和最小值這個問題，其實 Dijkstra 和很多最優化算法一樣，計算的是「最優值」，這個最優值可能是最大值，也可能是最小值。

標準 Dijkstra 算法是計算最短路徑的，但你有想過為什么 Dijkstra 算法不允許存在負權重邊么？

因為 Dijkstra 計算最短路徑的正確性依賴一個前提：路徑中每增加一條邊，路徑的總權重就會增加。

這個前提的數學證明大家有興趣可以自己搜索一下，我這里只說結論，其實你把這個結論反過來也是 OK 的：

如果你想計算最長路徑，路徑中每增加一條邊，路徑的總權重就會減少，要是能夠滿足這個條件，也可以用 Dijkstra 算法。

你看這道題是不是符合這個條件？邊和邊之間是乘法關系，每條邊的概率都是小于 1 的，所以肯定會越乘越小。

只不過，這道題的解法要把優先級隊列的排序順序反過來，一些 if 大小判斷也要反過來，我們直接看解法代碼吧：

double maxProbability（int n， int［］［］ edges， double［］ succProb， int start， int end） {

List《double［］》［］ graph = new LinkedList［n］;

for （int i = 0; i 《 n; i++） {

graph［i］ = new LinkedList《》（）;

}

// 構造鄰接表結構表示圖

for （int i = 0; i 《 edges.length; i++） {

int from = edges［i］［0］;

int to = edges［i］［1］;

double weight = succProb［i］;

// 無向圖就是雙向圖；先把 int 統一轉成 double，待會再轉回來

graph［from］.add（new double［］{（double）to， weight}）;

graph［to］.add（new double［］{（double）from， weight}）;

}

return dijkstra（start， end， graph）;

}

class State {

// 圖節點的 id

int id;

// 從 start 節點到達當前節點的概率

double probFromStart;

State（int id， double probFromStart） {

this.id = id;

this.probFromStart = probFromStart;

}

}

double dijkstra（int start， int end， List《double［］》［］ graph） {

// 定義：probTo［i］ 的值就是節點 start 到達節點 i 的最大概率

double［］ probTo = new double［graph.length］;

// dp table 初始化為一個取不到的最小值

Arrays.fill（probTo， -1）;

// base case，start 到 start 的概率就是 1

probTo［start］ = 1;

// 優先級隊列，probFromStart 較大的排在前面

Queue《State》 pq = new PriorityQueue《》（（a， b） -》 {

return Double.compare（b.probFromStart， a.probFromStart）;

}）;

// 從起點 start 開始進行 BFS

pq.offer（new State（start， 1））;

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curNodeID = curState.id;

double curProbFromStart = curState.probFromStart;

// 遇到終點提前返回

if （curNodeID == end） {

return curProbFromStart;

}

if （curProbFromStart 《 probTo［curNodeID］） {

// 已經有一條概率更大的路徑到達 curNode 節點了

continue;

}

// 將 curNode 的相鄰節點裝入隊列

for （double［］ neighbor ： graph［curNodeID］） {

int nextNodeID = （int）neighbor［0］;

// 看看從 curNode 達到 nextNode 的概率是否會更大

double probToNextNode = probTo［curNodeID］ * neighbor［1］;

if （probTo［nextNodeID］ 《 probToNextNode） {

probTo［nextNodeID］ = probToNextNode;

pq.offer（new State（nextNodeID， probToNextNode））;

}

}

}

// 如果到達這里，說明從 start 開始無法到達 end，返回 0

return 0.0;

}

好了，到這里本文就結束了，總共 6000 多字，這三道例題都是比較困難的，如果你能夠看到這里，真得給你鼓掌。

還是那句話，做題在質不在量，希望大家能夠透徹理解最基本的數據結構，以不變應萬變。

責任編輯：haq