2021年6月17日9時22分，搭載神舟十二號載人飛船的運載火箭，在酒泉衛(wèi)星發(fā)射中心點火發(fā)射。此后，神舟十二號載人飛船與火箭成功分離，進入預定軌道，順利將聶海勝、劉伯明、湯洪波3名航天員送入太空，發(fā)射取得圓滿成功。

在載人飛船運行的過程中，需要嚴格觀測及控制其運行軌跡。談到載人航天，不得不提及人類歷史上第一次登月，阿波羅登月，阿波羅號成功的背后是運用了卡爾曼濾波。

那什么是濾波？濾波是指從含有干擾的接收信號中提取有用信號的一種技術，是一種增強有用信號的數字信號處理過程。在數據通信中，無用信號表現為特定波段頻率和雜波，通常是一個隨機過程。卡爾曼濾波是最優(yōu)濾波中的一種常用算法，是以實現信號或狀態(tài)的最優(yōu)估值與相應的真實值的誤差的方差最小。

最早實現卡爾曼濾波器的是斯坦利·施密特。魯道夫·卡爾曼在訪問NASA埃姆斯研究中心時，將斯密特的方法應用于阿波羅計劃的軌道預測，并于1960年，提出離散系統(tǒng)卡爾曼濾波，后又將該種方法推廣到連續(xù)時間系統(tǒng)中。

正是由于卡爾曼濾波從時域分析處理數據，不僅可以處理平穩(wěn)隨機過程，也可以處理非平穩(wěn)隨機過程，所以被廣泛應用于各種領域，例如慣性導航，定位系統(tǒng)，經濟投資等。

卡爾曼濾波分類

常見的卡爾曼濾波主要分為離散型卡爾曼濾波和連續(xù)型卡爾曼濾波。

A.離散型卡爾曼濾波

遞推算法的使用是卡爾曼濾波的一大優(yōu)點，因此離散型卡爾曼濾波在工程上得到了廣泛的運用。在一個濾波周期內，根據卡爾曼濾波對使用系統(tǒng)信息和量測信息的先后次序，可以將卡爾曼濾波劃分為時間更新過程和量測更新過程，主要分為以下幾個部分。

1.一步預測：根據k-1時刻的狀態(tài)估計預測k時刻的狀態(tài)，通過k-1個時刻的量測量對k時刻狀態(tài)量進行線性最小方差估計。

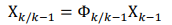
2.狀態(tài)估計方程：通過利用殘差（新息），對狀態(tài)量進行修正估計

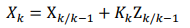
其中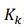，是對殘差的加權陣，被稱為濾波增益陣。

3.濾波增益陣和估計均方誤差陣的推導：最佳濾波增益陣使得估計的均方誤差達到最小。

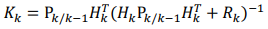
其中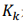，是最佳增益陣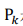，是最小均方誤差陣。

4.一步預測均方誤差陣推導

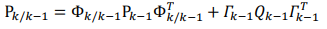
離散型卡爾曼濾波基本方程具有如下優(yōu)點：

（1）遞推算法的使用，使得數據的存儲量減少，通過濾波步數的增加，提取出的信息量在增大。

（2）只須知道驅動噪聲的統(tǒng)計特性，使得卡爾曼濾波能對非平穩(wěn)的被估計量做估計。

B．連續(xù)型卡爾曼濾波

連續(xù)型卡爾曼濾波可以在離散型卡爾曼濾波的基礎上進行推導，通過將連續(xù)系統(tǒng)離散化，應用離散型卡爾曼濾波基本方程和導數運算推導出連續(xù)型濾波方程。

設連續(xù)系統(tǒng)的系統(tǒng)方程和量測方程的一般形式為

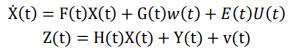
連續(xù)型卡爾曼濾波的預測和更新的一般方程為：

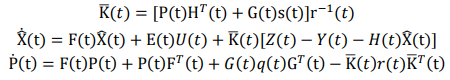
非線性系統(tǒng)卡爾曼濾波算法

A．擴展卡爾曼濾波

上述卡爾曼濾波問題都是假設物理系統(tǒng)的數學模型是線性的，但是線性模型只是理想化，實際工程中很多的模型都是非線性的。同時，在非線性系統(tǒng)中，如果系統(tǒng)噪聲和觀測噪聲都是任意分布，那么系統(tǒng)的處理難度會更大。因此，一般會對噪聲的統(tǒng)計特性給出符合實際而又便于數學處理的設定。非線性系統(tǒng)的數學模型如下

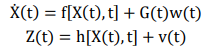
其中，w（t）和v（t）是彼此不相關的零均值白噪聲序列，它們與初始狀態(tài)X（0）也不相關。

針對擴展卡爾濾波，利用非線性函數的局部線性特性，將非線性模型局部線性化，通常是將非線性函數f圍繞濾波值做一階Taylor展開。

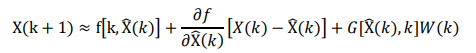
此外，將非線性函數h圍繞濾波值做一階Taylor展開。

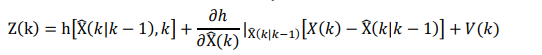
線性化后，對其運用線性卡爾曼濾波基本方程，便可獲得擴展卡爾曼濾波遞推方程。

B．無跡卡爾曼濾波

擴展卡爾曼濾波是對非線性的系統(tǒng)方程或者觀測方程進行泰勒展開并保留一階近似項，引入了線性化誤差。無跡卡爾曼濾波摒棄了對非線性函數進行線性化的傳統(tǒng)做法，采用卡爾曼線性濾波框架，對于一步預測方程，使用無跡變換來處理均值和協方差的非線性傳遞問題。

什么是無跡變換呢？在原狀態(tài)分布中按照某一規(guī)則選取一些采樣點，他們的均值和協方差等于原狀態(tài)分布的均值和協方差；并將他們帶入非線性函數，獲取相應函數值的點集。對這些點求取變換后的均值和協方差。

針對無跡卡爾曼濾波，其非線性系統(tǒng)的描述

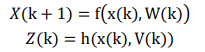
根據上述無跡變換，對非線性系統(tǒng)進行變換處理。不同于在估計點處做Taylor級數展開，再進行n階近似，而是在估計點附件進行無跡變換，使得Sigma點集的均值和協方差與原統(tǒng)計特性匹配，再對這些Sigma點集進行非線性映射，獲得狀態(tài)概率密度函數，實現一種統(tǒng)計近似。

C.交互式多模型卡爾曼濾波

針對前面幾種卡爾曼濾波，不必知道目標的運動模型就能夠實時修正目標的狀態(tài)參量，具有較好的適應性，但是如果目標實施突然的運動變化時，基本的卡爾曼濾波就無法獲取好的結果了。交互式多模型卡爾曼濾波是一種軟切換算法，使用兩個或者更多的模型描述工作過程中的狀態(tài)，利于減小單模型估計誤差較大的影響。

交互式多模型卡爾曼濾波的思想是在每一個時刻，假設某個模型在當下時刻有效，然后混合前一時刻所有濾波器的狀態(tài)估計值，獲取與這個特定模型匹配的濾波器的初始條件，然后對每個模型并行實施濾波，然后，以模型匹配似然函數為基礎更新模型概率，并組合所有濾波器修正后的狀態(tài)估計值以得到狀態(tài)估計。

在使用該算法時，對于濾波器的目標運動模型的選擇，需要從以下幾個方面進行考慮。

1.濾波器個數的選擇，包括較為精確的模型和較為粗糙的模型。

2.馬爾科夫鏈狀態(tài)轉移概率的選取對濾波器的性能有較大影響，會直接影響模型誤差和模型概率估計的準確性。

3.該算法具有模塊化的特性，當使用的時候，無法預料目標的運動規(guī)律時，應該選擇一般的魯棒性較強的模型。

作者：凌霄

浙江大學機械電子專業(yè)博士，從事智能傳感與人機交互，智能機器人控制等領域的研究

編輯：jq