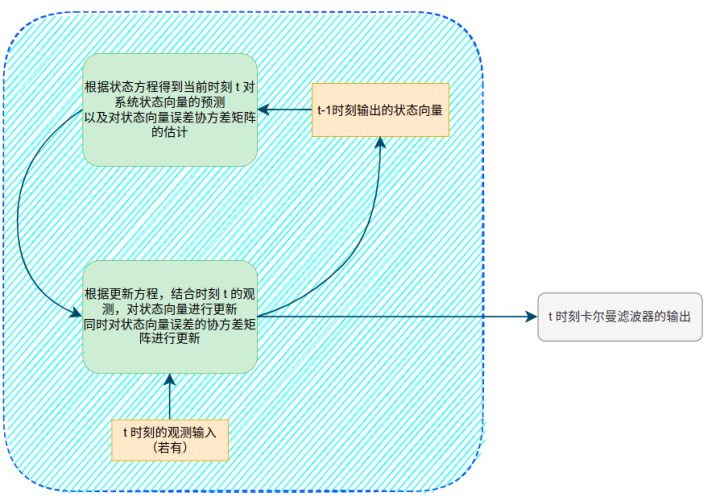
卡爾曼濾波(Kalman Filter)是一種線性動態(tài)系統(tǒng)的狀態(tài)估計算法,廣泛應(yīng)用于信號處理、導航、控制等領(lǐng)域。
- 卡爾曼濾波的優(yōu)點
1.1 高效性
卡爾曼濾波是一種遞歸算法,可以在實時系統(tǒng)中高效地進行狀態(tài)估計。它只需要存儲當前時刻的狀態(tài)估計和誤差協(xié)方差,而不需要存儲整個觀測序列,從而節(jié)省了計算資源和存儲空間。
1.2 魯棒性
卡爾曼濾波對系統(tǒng)模型和觀測模型的不確定性具有一定的魯棒性。即使模型存在一定的誤差,卡爾曼濾波仍然能夠提供較為準確的狀態(tài)估計。此外,卡爾曼濾波還可以通過調(diào)整過程噪聲和觀測噪聲的協(xié)方差來適應(yīng)不同的系統(tǒng)特性。
1.3 準確性
在線性高斯系統(tǒng)下,卡爾曼濾波能夠提供最優(yōu)的狀態(tài)估計。它利用最小二乘法最小化估計誤差的方差,從而實現(xiàn)對系統(tǒng)狀態(tài)的準確估計。在許多實際應(yīng)用中,卡爾曼濾波的估計精度已經(jīng)得到了廣泛認可。
1.4 可擴展性
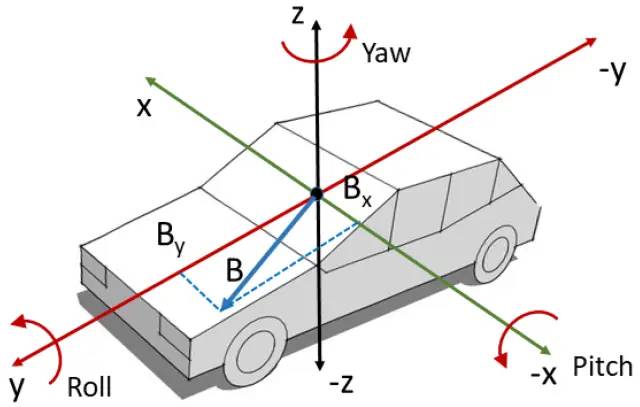
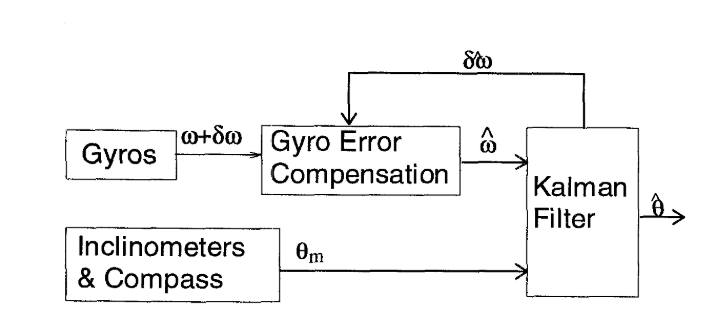
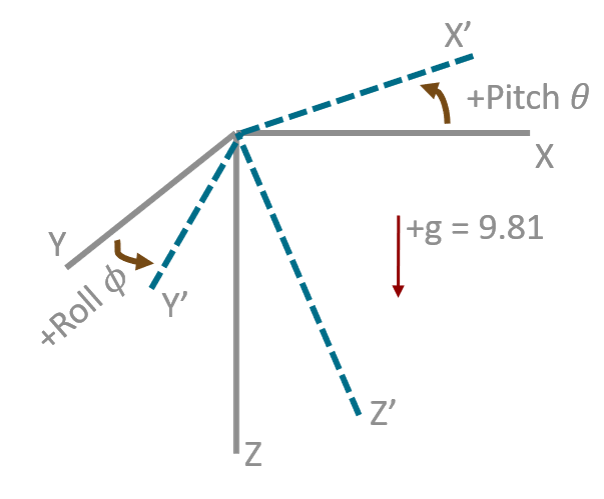
卡爾曼濾波可以擴展到更復雜的系統(tǒng),如非線性系統(tǒng)和多變量系統(tǒng)。通過引入擴展卡爾曼濾波(EKF)和無跡卡爾曼濾波(UKF)等變體,卡爾曼濾波可以應(yīng)用于更廣泛的領(lǐng)域。
1.5 易于實現(xiàn)
卡爾曼濾波的算法相對簡單,易于實現(xiàn)。許多編程語言和數(shù)學軟件包都提供了卡爾曼濾波的實現(xiàn),使得用戶可以快速地將其應(yīng)用于實際問題。
- 卡爾曼濾波的缺點
2.1 線性系統(tǒng)限制
卡爾曼濾波的基本假設(shè)是系統(tǒng)和觀測模型是線性的,且噪聲是高斯分布的。然而,在許多實際應(yīng)用中,系統(tǒng)可能存在非線性特性,這會導致卡爾曼濾波的估計精度下降。
2.2 模型誤差敏感性
卡爾曼濾波對系統(tǒng)模型和觀測模型的誤差非常敏感。如果模型存在較大的誤差,卡爾曼濾波的估計結(jié)果可能會受到很大的影響。因此,在實際應(yīng)用中,需要對模型進行精確的建模和校準。
2.3 計算復雜性
雖然卡爾曼濾波的算法相對簡單,但在處理高維系統(tǒng)時,其計算復雜性可能會變得很高。特別是在擴展卡爾曼濾波和無跡卡爾曼濾波中,由于需要對非線性函數(shù)進行線性化和積分,計算量可能會顯著增加。
2.4 初始狀態(tài)敏感性
卡爾曼濾波對初始狀態(tài)的估計非常敏感。如果初始狀態(tài)估計不準確,可能會導致濾波器的收斂速度變慢,甚至無法收斂。因此,在實際應(yīng)用中,需要對初始狀態(tài)進行合理的估計和調(diào)整。
2.5 對噪聲的假設(shè)限制
卡爾曼濾波假設(shè)過程噪聲和觀測噪聲是高斯分布的,且具有已知的協(xié)方差。然而,在實際應(yīng)用中,噪聲的分布可能并不符合高斯分布,或者協(xié)方差未知。這可能會導致卡爾曼濾波的估計精度下降。
- 結(jié)論
卡爾曼濾波作為一種經(jīng)典的狀態(tài)估計算法,在許多領(lǐng)域得到了廣泛的應(yīng)用。它具有高效性、魯棒性、準確性、可擴展性和易于實現(xiàn)等優(yōu)點。然而,它也存在一些缺點,如線性系統(tǒng)限制、模型誤差敏感性、計算復雜性、初始狀態(tài)敏感性和對噪聲的假設(shè)限制等。
-
存儲
+關(guān)注
關(guān)注
13文章
4467瀏覽量
86887 -
信號處理
+關(guān)注
關(guān)注
48文章
1054瀏覽量
103798 -
非線性系統(tǒng)
+關(guān)注
關(guān)注
0文章
20瀏覽量
7937 -
卡爾曼濾波
+關(guān)注
關(guān)注
3文章
166瀏覽量
24913
發(fā)布評論請先 登錄
相關(guān)推薦
卡爾曼濾波有哪些應(yīng)用
卡爾曼濾波簡介
卡爾曼濾波的變種有哪些?1
卡爾曼濾波的變種有哪些?2
卡爾曼濾波的變種有哪些?3
卡爾曼濾波的變種有哪些?4







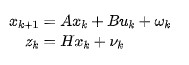
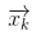
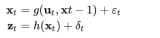











評論