在CNN中，轉(zhuǎn)置卷積是一種上采樣(up-sampling)的方法。如果你對(duì)轉(zhuǎn)置卷積感到困惑，那么就來(lái)讀讀這篇文章吧。

上采樣的需要

在我們使用神經(jīng)網(wǎng)絡(luò)的過(guò)程中，我們經(jīng)常需要上采樣(up-sampling)來(lái)提高低分辨率圖片的分辨率。

上采樣有諸多方法，舉例如下。
最近鄰插值(Nearest neighbor interpolation)
雙線性插值(Bi-linear interpolation)
雙立方插值(Bi-cubic interpolation)

但是，上述的方法都需要插值操作，而這些插值的操作都充滿了人為設(shè)計(jì)和特征工程的氣息，而且也沒有網(wǎng)絡(luò)進(jìn)行學(xué)習(xí)的余地。

為何需要轉(zhuǎn)置卷積

如果我們想要網(wǎng)絡(luò)去學(xué)出一種最優(yōu)的上采樣方法，我們可以使用轉(zhuǎn)置卷積。它與基于插值的方法不同，它有可以學(xué)習(xí)的參數(shù)。

若是想理解轉(zhuǎn)置卷積這個(gè)概念，可以看看它是如何運(yùn)用于在一些有名的論文和項(xiàng)目中的。

DCGAN的生成器(generator)接受一些隨機(jī)采樣的值作為輸入來(lái)生成出完整的圖片。它的語(yǔ)義分割(semantic segmentation)就使用了卷積層來(lái)提取編碼器(encoder)中的特征，接著，它把原圖存儲(chǔ)在解碼器(decoder)中以確定原圖中的每個(gè)像素的類別歸屬。

轉(zhuǎn)置卷積也被稱作: “分?jǐn)?shù)步長(zhǎng)卷積(Fractionally-strided convolution)”和”反卷積(Deconvolution)”.

我們?cè)谶@篇文章里面只使用轉(zhuǎn)置卷積這個(gè)名字,其他文章可能會(huì)用到其他名字. 這些名字指的都是同樣的東西.

卷積操作

我們先通過(guò)一個(gè)簡(jiǎn)單的例子來(lái)看看卷積是怎么工作的.

假設(shè)我們有一個(gè)4x4的input矩陣, 并對(duì)它使用核(kernel)為3x3,沒有填充(padding),步長(zhǎng)(stride)為1的卷積操作. 結(jié)果是一個(gè)2x2的矩陣,如下圖所示.

(譯者注: stride,kernel,padding等詞以下記為英文)

卷積操作的本質(zhì)其實(shí)就是在input矩陣和kernel矩陣之間做逐元素(element-wise)的乘法然后求和. 因?yàn)槲覀兊膕tride為1,不使用padding,所以我們只能在4個(gè)位置上進(jìn)行操作.

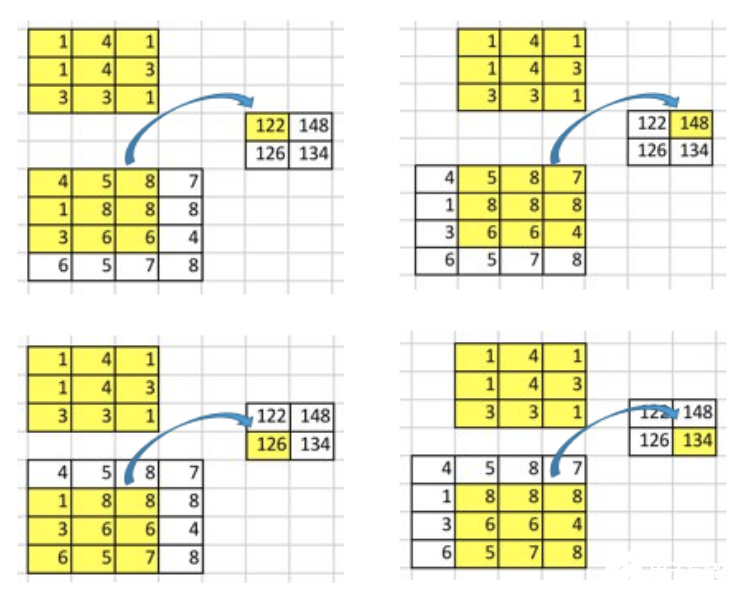
要點(diǎn)：卷積操作其實(shí)就是input值和output值的位置性關(guān)系(positional connectivity).

例如,在input矩陣的左上角的值會(huì)影響output矩陣的左上角的值.

更進(jìn)一步,3x3的核建立了input矩陣中的9個(gè)值和output矩陣中的1個(gè)值的關(guān)系.

“卷積操作建立了多對(duì)一的關(guān)系”. 在閱讀下文時(shí),請(qǐng)讀者務(wù)必時(shí)刻牢記這個(gè)概念.

卷積的逆向操作

現(xiàn)在,考慮一下我們?nèi)绾螕Q一個(gè)計(jì)算方向. 也就是說(shuō),我們想要建立在一個(gè)矩陣中的1個(gè)值和另外一個(gè)矩陣中的9個(gè)值的關(guān)系.這就是像在進(jìn)行卷積的逆向操作,這就是轉(zhuǎn)置卷積的核心思想.

(譯者注:從信息論的角度看,卷積是不可逆的.所以這里說(shuō)的并不是從output矩陣和kernel矩陣計(jì)算出原始的input矩陣.而是計(jì)算出一個(gè)保持了位置性關(guān)系的矩陣.)

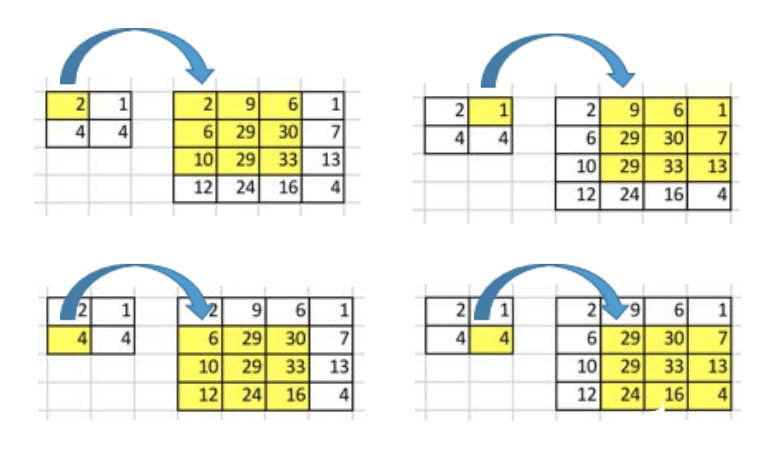
但是,我們?nèi)绾芜M(jìn)行這種逆向操作呢?

為了討論這種操作,我們先要定義一下卷積矩陣和卷積矩陣的轉(zhuǎn)置.

卷積矩陣

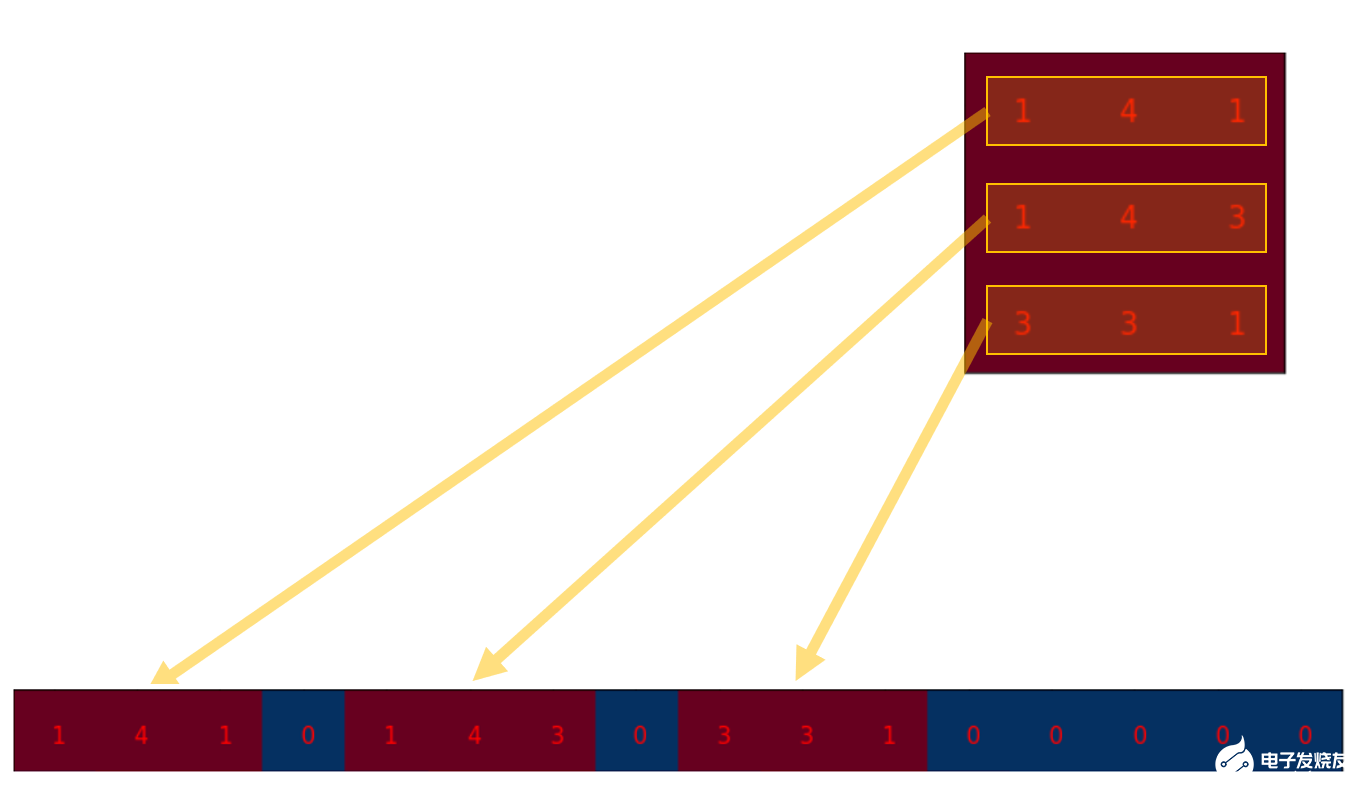
我們可以將卷積操作寫成一個(gè)矩陣. 其實(shí)這就是重新排列一下kernel矩陣, 使得我們通過(guò)一次矩陣乘法就能計(jì)算出卷積操作后的矩陣.

我們將3x3的kernel重排為4x16的矩陣,如下:

這就是卷積矩陣. 每一行都定義了一次卷積操作. 如果你還看不透這一點(diǎn), 可以看看下面的圖. 卷積矩陣的每一行都相當(dāng)于經(jīng)過(guò)了重排的kernel矩陣,只是在不同的位置上有zero padding罷了.

為了實(shí)現(xiàn)矩陣乘法,我們需要將尺寸為4x4的input矩陣壓扁(flatten)成一個(gè)尺寸為16x1的列向量(column vector).

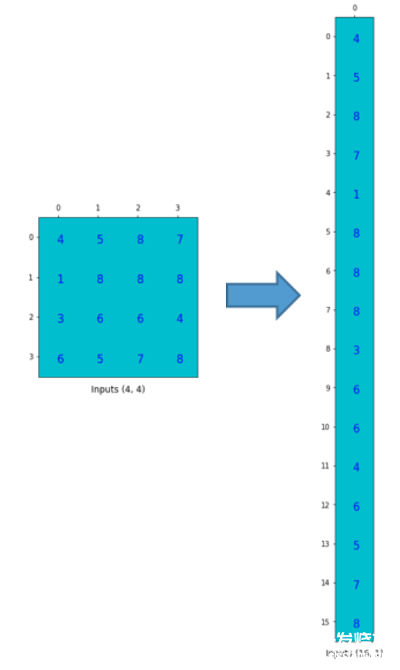
然后,我們對(duì)4x16的卷積矩陣和1x16的input矩陣(就是16維的列向量,只是看成一個(gè)矩陣)進(jìn)行矩陣乘法.

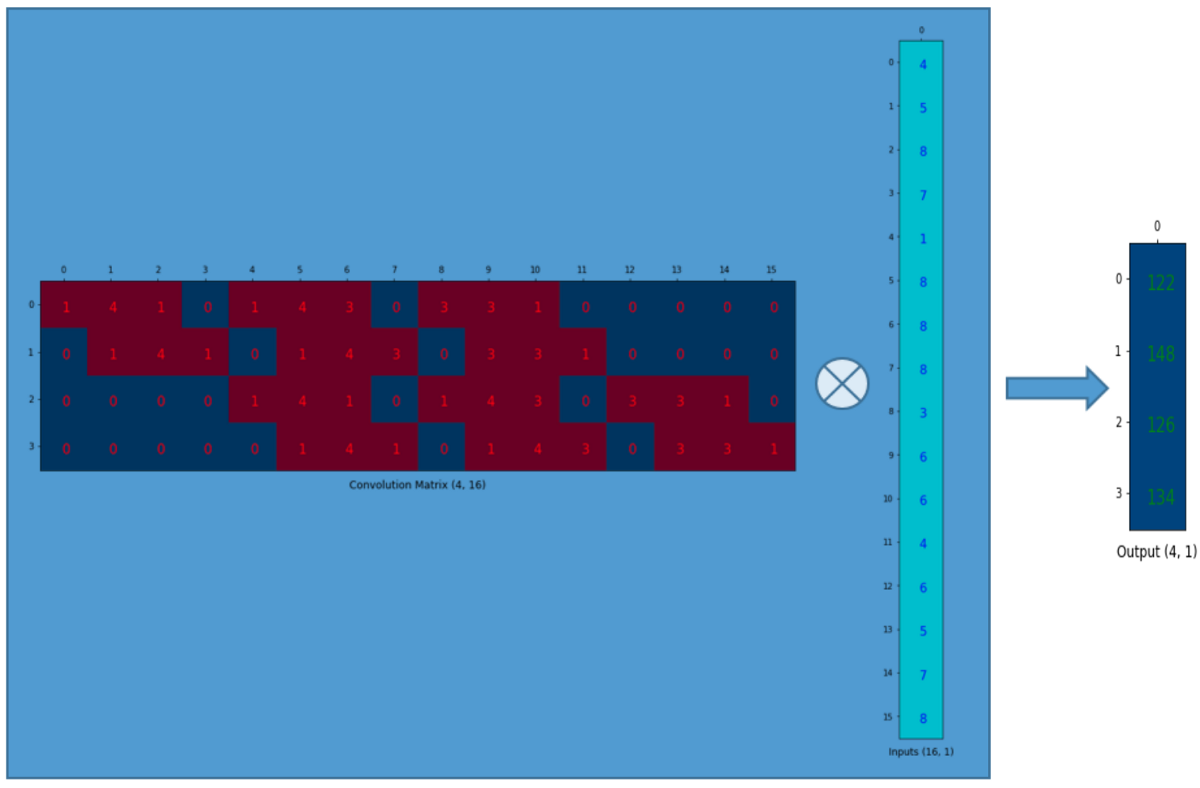
尺寸為4x1的output矩陣可以重排為2x2的矩陣.這正和我們之前得到的結(jié)果一致.

一句話,一個(gè)卷積矩陣其實(shí)就是kernel權(quán)重的重排,一個(gè)卷積操作可以被寫成一個(gè)卷積矩陣.

即便這樣又如何呢?

我想說(shuō)的是: 使用這個(gè)卷積矩陣,你可以把16(4x4的矩陣)個(gè)值映射為4(2x2的矩陣)個(gè)值. 反過(guò)來(lái)做這個(gè)操作,你就可以把4(2x2的矩陣)個(gè)值映射為16(4x4的矩陣)辣.

蒙了?

繼續(xù)讀.

轉(zhuǎn)置過(guò)后的卷積矩陣

我們想把4(2x2的矩陣)個(gè)值映射為16(4x4的矩陣)個(gè)值。但是，還有一件事！我們需要維護(hù)1對(duì)9的關(guān)系。

假設(shè)我們轉(zhuǎn)置一下卷積矩陣C(4x16)，得到C.T(16x4)。我們可以將C.T(16x4)和一個(gè)列向量(4x1)以矩陣乘法相乘，得到尺寸為16x1的output矩陣。轉(zhuǎn)置之后的矩陣建立了1個(gè)值對(duì)9個(gè)值的關(guān)系。

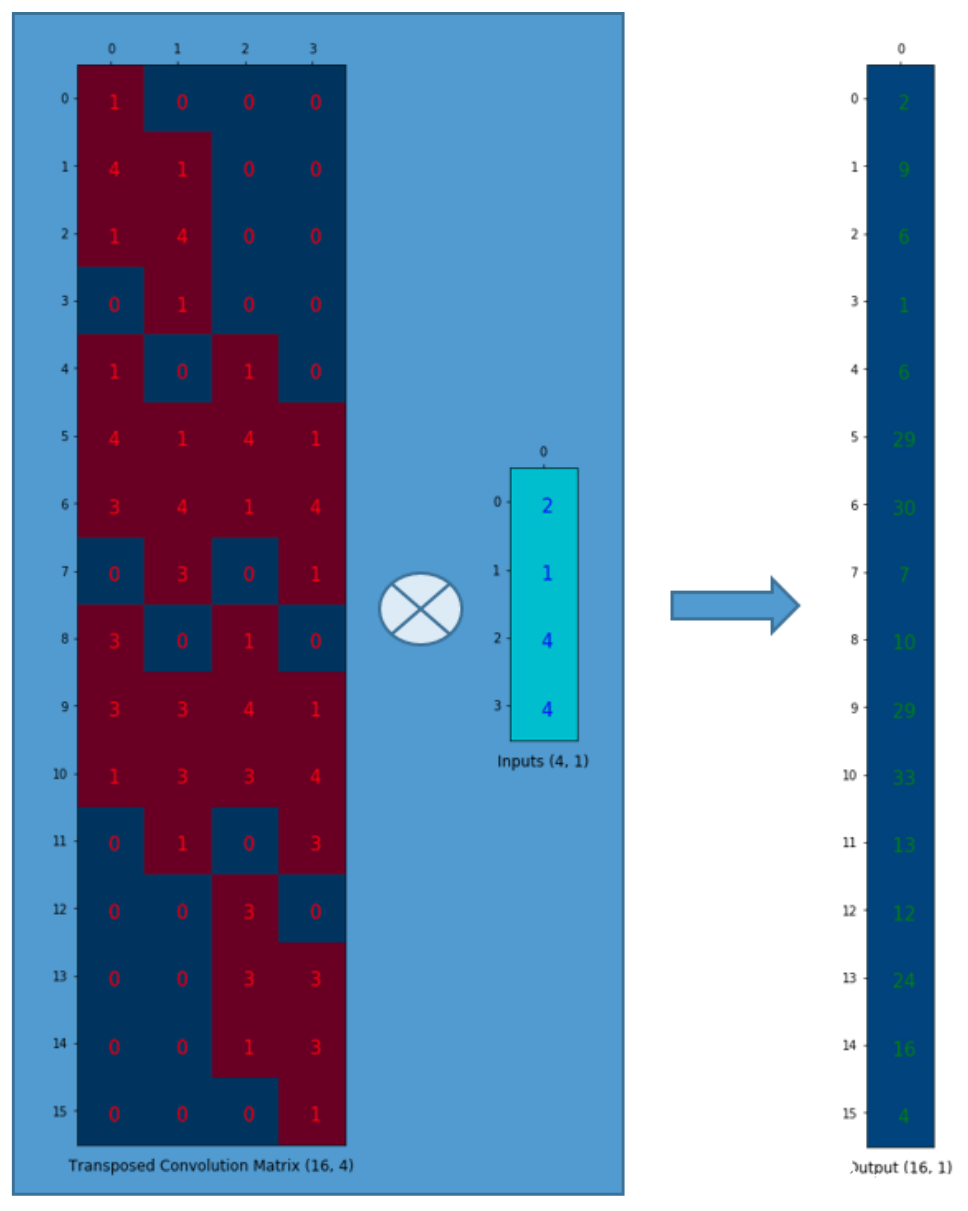
output矩陣可以被重排為4x4的.

我們已經(jīng)上采樣了一個(gè)小矩陣(2x2)，得到了一個(gè)大矩陣(4x4)。轉(zhuǎn)置卷積依然維護(hù)著1對(duì)9的關(guān)系：因?yàn)闄?quán)重就是這么排的。

注意：用來(lái)進(jìn)行轉(zhuǎn)置卷積的權(quán)重矩陣不一定來(lái)自于(come from)原卷積矩陣。重點(diǎn)是權(quán)重矩陣的形狀和轉(zhuǎn)置后的卷積矩陣相同。

總結(jié)

轉(zhuǎn)置卷積和普通卷積有相同的本質(zhì)：建立了一些值之間的關(guān)系。只不過(guò)，轉(zhuǎn)置卷積所建立的這個(gè)關(guān)系與普通卷積所建立的關(guān)系，方向相反。

我們可以使用轉(zhuǎn)置卷積來(lái)進(jìn)行上采樣。并且，轉(zhuǎn)置卷積中的權(quán)重是可以被學(xué)習(xí)的。因此，我們沒有必要搞什么插值方法來(lái)做上采樣。

盡管它被稱作轉(zhuǎn)置卷積，但是這并不意味著我們是拿一個(gè)已有的卷積矩陣的轉(zhuǎn)置來(lái)作為權(quán)重矩陣的來(lái)進(jìn)行轉(zhuǎn)置卷積操作的. 和普通卷積相比，intput和output的關(guān)系被反向處理(轉(zhuǎn)置卷積是1對(duì)多，而不是普通的多對(duì)1)，才是轉(zhuǎn)置卷積的本質(zhì)。

正因如此，嚴(yán)格來(lái)說(shuō)轉(zhuǎn)置卷積其實(shí)并不算卷積。但是我們可以把input矩陣中的某些位置填上0并進(jìn)行普通卷積來(lái)獲得和轉(zhuǎn)置卷積相同的output矩陣。你可以發(fā)現(xiàn)有一大把文章說(shuō)明如何使用這種方法實(shí)現(xiàn)轉(zhuǎn)置卷積。然而，因?yàn)樾枰诰矸e操作之前，往input中填上許多的0，這種方法其實(shí)有點(diǎn)效率問(wèn)題.

警告：轉(zhuǎn)置卷積會(huì)在生成的圖像中造成棋盤效應(yīng)(checkerboard artifacts)。本文推薦在使用轉(zhuǎn)置卷積進(jìn)行上采樣操作之后再過(guò)一個(gè)普通的卷積來(lái)減輕此類問(wèn)題。如果你主要關(guān)心如何生成沒有棋盤效應(yīng)的圖像，需要讀一讀paper。