在大多數情況下,開關電源(SMPS)反饋環路通過觀測特定點上的電壓來進行穩壓,而其余輸出電壓則依靠變壓器的性能來確保正常運行。在這種情況下,穩定性分析必須包含所有次級元件,以涵蓋所有可能的負載配置。毋庸置疑,涵蓋所有可能的輸入/輸出情況的傳統分析方法難度高且耗時長,簡化分析也容易出錯。本文將介紹采用SPICE仿真器進行多輸出電源穩定性分析的簡化方法。

簡單的反射
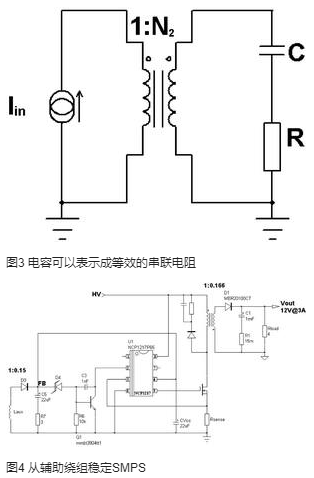
電阻連接到變壓器次級端時,初級端可以“看到”一個等效電阻,如圖1所示,其中匝數比在初級歸一化。歸一化表示將所有比例除以初級匝數比:Np:Ns=10:5,在歸一化之后表示為1:0.5。
若變壓器性能卓越(Imag=0),則可得出:
1 x I1=N2 x I(方程1),且V2=V1 x N2(方程2)或V1 / V2=1 / N2(方程3)。
因為I2=V2 / RL(方程4),可將方程4代入方程1,得出:
I1=V1 / Req=N2 x V2 / RL(方程5)。重新排列該方程得出:Req=V1 x RL / N2 x V2(方程6)。
根據方程3,最后得到:Req=RL / N22(方程7)。
在這種情況下,變壓器變成繞組,簡化了分析。
首先用方程7將RL2反射到初級端:Req1=RL2 / N32(方程8)。那么,逆方向應用方程7,將Req1“推至”RL1上:Req2=Req1 x N22=RL2 x N22 / N32。最后,可以得出Req的計算方程:Req=RL1 // [ RL2 x (N2/N3)2 ](方程9)。
除了電阻以外,還可以反射為—簡單的電容。在這種情況下,對于正弦波激勵,電容阻抗為Zc=1 / j x C x ?(方程10),此時仍可采用方程7:Ceq=1 / j x C x ??x N22或Ceq=C x N22(方程11)。
在圖2a中,將阻抗反射到另一個繞組。采用方程10和7,可以得出Ceq=(1 / j x C x ?) x [N2/N3]2或Ceq=C x [N3 / N2]2(方程12)。注意,該方程與方程9互逆。
如果根據上述結論討論阻抗,給定阻抗反射到初級端的結果可利用下列方程進行計算:
Zeq=Zload x (N1/N2)2(方程12b)假設N1=1,那么對于電阻,Zeq=Rload x (1/N2)2(方程12c)。對于電容,Zeq=1 / (2 x ? x f x Cload x N22)(方程12d)。對于電感,Zeq=2 x ??x f x Lload / N22(方程12e)。
電容始終與等效的串聯電阻(ESR)相連,如圖3所示。電容C和電阻R串聯起來可得到復導納Y,計算方程為:
Y=或(方程13)。若網絡時間常數?=R x C,則其阻抗(方程14)。如果采用方程7,則初級端的等效阻抗為:
(方程15)。
當兩個受到各自ESR影響的電容并聯時,就會產生復阻抗并聯現象。然而,通過這種元件組合得到的總阻抗沒有簡單的表達式。阻抗并聯時的導納表達式為:
1. 假設 R1 x C1=R2 x C2
設Y1是R1.C1的導納,而Y2是R2.C2的導納。因此,Ytot=Y1+Y2
Ytot==
=(方程16)。采用方程13中的符號,方程16可以改寫為:Ytot=。如果?1=?2=?,那么最后的導納可簡化為:Ytot= (方程17),它與方程13相似,方程13中電容C是兩個電容的和(和并聯一樣),且ESR的值若與(C1+C2)結合,則可得出?1或?2的值。電阻Req=?1 / (C1 + C2),可以從中推出Req=R1 // R2(因為若F→埃?蛄礁齙縟荻冀?搪 )。
因此,并聯兩個時間常數相同的串聯RC網絡R1-C1和 R2-C2時,產生的等效串聯RC網絡由C=C1+C2和R=R1 // R2組成。
2.假設R1 x C1≠R2 x C2
根據方程16,簡化表達式中的p并且忽略其中的1后得出:
Ytot=(方程18),與方程13明顯不同。
總之,時間常數不同的兩個并聯RC網絡不能簡化成一個RC網絡。
將反射應用于初級穩壓電源
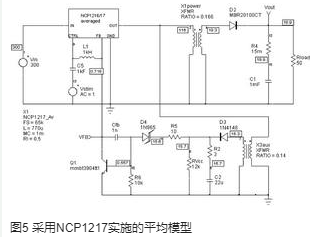
在初級穩壓電源應用中,輔助繞組不僅提供控制器的電源Vcc,還提供輸出電壓的鏡象。若兩個繞組之間的耦合質量良好,則電平相互之間的追蹤便能取得良好的效果。圖4為采用NCP1217設計的反擊電源。用齊納二極管和低成本的雙極型元件Q1確保反饋。由于反饋電平必須降低以減少功耗,因此該晶體管是必需的。穩壓點實際上是D4的陽極、電路Vcc引腳載入的FB點。首先應將所有次級元件反射到初級端,將轉換器簡化為單個輸出的版本。請注意:負載和控制器功耗一起反射,如同電阻在FB點上工作,而且在反射過程中,認為D1和D3的動態電阻接近零。
反射步驟為:
1. 將4?負載反射到輔助繞組:4×(0.15 / 0.166)2=3.26?
2. 將輸出電容反射到輔助繞組:1×(0.166 / 0.15)2=1.22mF
3. 用簡單的電阻增加芯片功耗:12V/1mA=12k?
4. 由于電容和ESR的時間常數接近,因此可以將兩者合并。
在最后的反射上可以定位典型極點和零點,這兩點位于在非連續導電模式(DCM)中工作的反擊轉換器中。
注意:Rload可以用更簡單的方法推出。匝數比已知時,12V輸出的反饋電壓為12×(0.15/0.166)= 10.84V。若在輸出上提供3A電流,則功率為36W。從輔助/FB電平來看,其等效負載為P=U2/R或 Req=10.842 / 36=3.26?。
SPICE適用于很多情況
一般的SPICE模型使SMPS的穩定性測試變得很簡單。測試時無需反射電容、負載、電阻等,也無需調整并聯組合:這一切都由SPICE自動完成。在本文的實例中,需要收集反擊段模型(電流或電壓模式),然后用原理圖完成變壓器配置。圖4的仿真電路如圖5所示。
通過在輸出上安裝開關并且逐步將它載入的方法,可以檢查電源的穩定性。此外還可以比較周期間仿真的結果以驗證該平均配置。
電路上的功率MOSFET被行為級開關代替,以加速仿真時間。通過觀測開關啟動時的輸出電壓,可以比較平均模型和周期間應用的瞬態響應。
結語
本文分析了對開關模式轉換器(包括寄生元件,如輸出二極管的動態電阻)進行綜合穩定性分析的重要性。若不進行分析,在預測極點和零點位置時將產生較大誤差。隨著轉換器日益復雜(如增加次級電感濾波器),傳統的手工分析變得極為復雜。而SPICE提供了分析所需的靈活性,同時考慮到反射和動態電阻,使工程師可像處理真實電路一樣設置仿真模板,并且順利地進行AC分析。
責任編輯:gt
 電子發燒友App
電子發燒友App























評論