穩定系統簡介
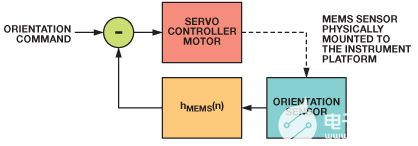
無人飛行器安裝的監控設備、海上微波接收機、車輛安裝的紅外成像系統傳感器以及其他儀器系統都需要具有穩定的平臺,以達到最佳性能,但它們通常在可能遇到振動和其他類型不良運動的應用中使用。振動和正常車輛運動會導致通信中斷、圖像模糊以及其他很多行為,從而降低儀器的性能和執行所需功能的能力。平臺穩定系統采用閉環控制系統,以主動消除此類運動,從而保證達到這些儀器的重要性能目標。圖1是平臺穩定系統的整體框圖,它使用伺服電機來校正角向運動。反饋傳感器為儀器平臺提供動態方位信息。反饋控制器處理這些信息,并將其轉換為伺服電機的校正控制信號。

?
圖1. 基本平臺穩定系統。
由于很多穩定系統需要多個軸向的主動校正,因此慣性測量單元(IMU)通常包括至少三個軸向的陀螺儀(測量角速度)和三個軸向的加速度計(測量加速度和角定向)來提供反饋檢測功能。反饋傳感器的最終目標是提供平臺定向的精確測量,即使當平臺正在運動時也要做到。由于沒有“萬能”傳感器技術能夠在任何條件下提供精確的角度測量,因此平臺穩定系統中的IMU通常在每個軸上使用兩種或三種傳感器類型。
加速度計響應每個軸向上的靜態和動態加速。“靜態加速度”似乎是一個陌生的詞匯,但它涉及重要的傳感器行為:對重力的響應。假定不存在動態加速,并通過校準消除了傳感器誤差,則每個加速度計輸出將代表它的相對于重力的軸定向。為了確定在存在振動和快速加速的情況下穩定系統中通常出現的實際平均定向,通常會將濾波器和融合程序(組合來自多個傳感器類型的讀數,得出最佳估計值)應用于原始測量
另一種類型的傳感器是陀螺儀,它提供角速率測量。陀螺儀測量通過有限周期內的角速率的積分,在角度測量中發揮作用。執行積分時,偏置誤差將導致成比例的角度漂移,隨時間累加。因此,陀螺儀性能通常與設備偏置對不同環境因素的靈敏度相關,這些因素包括溫度變化、電源變化、離軸旋轉和線性加速度(線性g和整流g × g)。校準的高質量陀螺儀,具有對線性加速度的高抑制,使這些設備能夠提供寬帶角信息,作為對加速度計提供的低頻信息的補充。
第三種類型的傳感器是3軸磁力計,它可以測量磁場強度。從三個正交軸的磁場測量實現了相對于地球磁場本地方向的定向角估算。當磁力計接近電機、顯示器和其他動態磁場干擾源時,管理其精度可能非常困難,但在適當情況下,它的角度數據可作為來自加速度計和陀螺儀的數據的補充。雖然很多系統僅使用加速度計和陀螺儀,但磁力計可以改進某些系統的測量精度。
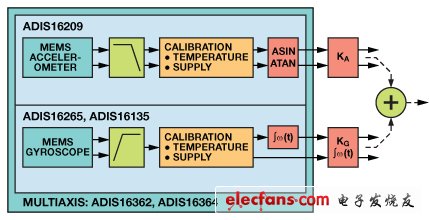
圖2的整體框圖顯示了如何使用陀螺儀和加速度計測量,既利用它們的基本優勢,同時又最大程度減少它們的弱點產生的影響。低通加速度計和高通陀螺儀濾波器的極點位置通常取決于應用,另外精度目標、相位延遲、振動和“正常”運動預測都會對位置決定產生影響。因系統而異的行為也會影響加權因子,而加權因子會對如何組合這兩種測量產生影響。擴展卡爾曼濾波器就是一個組合濾波和加權函數以計算動態角度估計的算法的例子。
?
圖2. 組合單軸傳感器輸出。
MEMS IMU頻率響應分析
圍繞新的MEMS IMU開發穩定系統時,在系統設計早期階段了解頻率響應是非常重要的,因為IMU的頻率響應將對控制器設計產生直接影響,可以幫助識別潛在穩定性問題—特別是在考慮到新一代設計的高帶寬解決方案時。這些信息對于預測陀螺儀的振動響應也非常有用。
評估IMU帶寬的一種策略是確定哪些信息在產品文檔中提供,分析此類信息對系統的慣性運動響應的影響,并穩定系統的響應。此類分析以及它涉及的所有校正操作將成為初始測試的基礎。
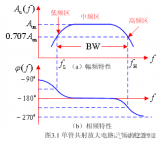
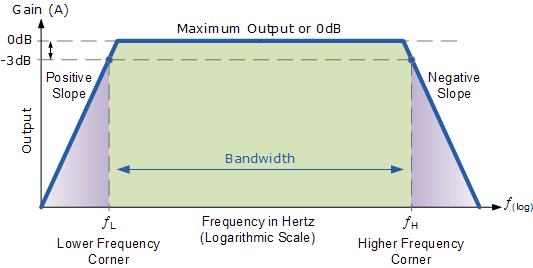
率響應在IMU和陀螺儀的規格表中表示為“帶寬”。作為一個性能參數,它表示某個頻率,輸出信號幅度在該頻率下降低到傳感器遇到的實際運動幅度的大約70% (–3 dB)。某些情況下,帶寬可也定義為輸出響應落后于實際運動90度時的頻率(對于雙極系統)。這兩個指標可以直接影響控制環路的一個重要穩定準則:單位增益、相位裕量—環路響應的實際相位角度和–180°之間的差值,環路增益為1。了解反饋傳感器的頻率響應,是優化穩定性保證和系統響應之間的平衡的關鍵因素。除了管理穩定性標準之外,頻率響應還會對振動抑制和制定采樣策略產生直接影響,通過這些策略可以測量慣性平臺上的所有關鍵瞬態信息。
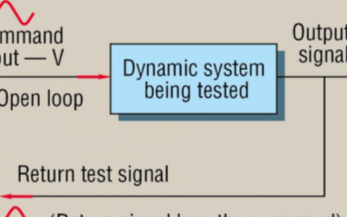
要分析系統中的頻率響應,首先要從一個高層次“黑盒子”視圖開始,它描述了系統在整個目標頻率范圍內對輸入的響應。在電子電路中,輸入和輸出是從一般意義上定義的,例如信號電平(伏特),分析通常包括開發傳遞函數,使用s域表示和電路-電平關系,例如基爾霍夫的電壓和電流定律。對于慣性MEMS系統,輸入是IMU遇到的慣性運動,輸出通常以數字碼表示。s域分析技術固然有很大作用,但要為這種類型的系統開發完整的傳遞函數,通常還需要采用其他技術,并且考慮到更多問題。
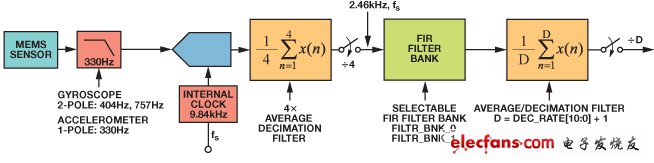
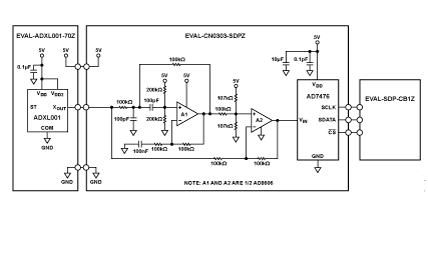
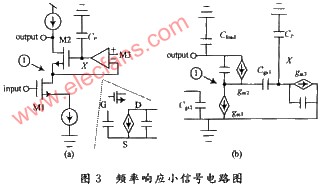
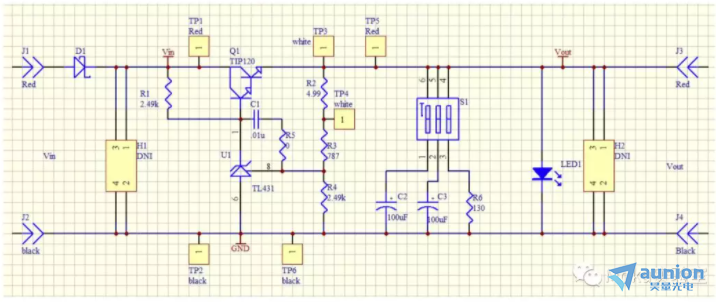
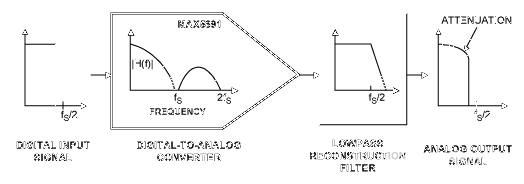
開始分析過程時,首先要了解與傳感器信號鏈相關的所有組件。圖3提供了典型函數的整體示意圖。信號鏈從核心傳感器元件開始,它將慣性運動轉化為代表性的電信號。如果帶寬在傳感器元件中未受限制,則通常受ADC模塊前的信號調理電路中的濾波器限制。信號數字化后,處理器通常應用糾錯(校準)公式和數字濾波。第二級的數字濾波器會減小反饋系統在控制程序中使用的帶寬和采樣速率。所有這些級都可能影響傳感器信號的增益和相位,與頻率相關。圖3提供了一個示例,IMU在混合信號處理系統中具有多個濾波器。該系統可作為一些實用分析技術的示例。
?
圖3. 信號鏈中用于頻率分析的ADIS16488傳感器。
核心MEMS傳感器元件
要進行此類分析,必須了解可以量化和應該量化的所有行為,然后可對那些無法輕易量化的行為做出合理假設。充分了解“已知”可變因素之后,通常可以更加簡單地重新評估這些假設以進行檢查和澄清。ADIS16488 的規格表(圖3)顯示了330 Hz的–3 dB帶寬。假定核心傳感器處于臨界阻尼狀況,而且在遠低于其諧振范圍(16 kHz至20 kHz)的帶寬下并非主要貢獻因素。這種情況并非總會出現,但它是一個很好的起點,可以使用噪聲密度或完全運動測試,稍后在流程中測試到。
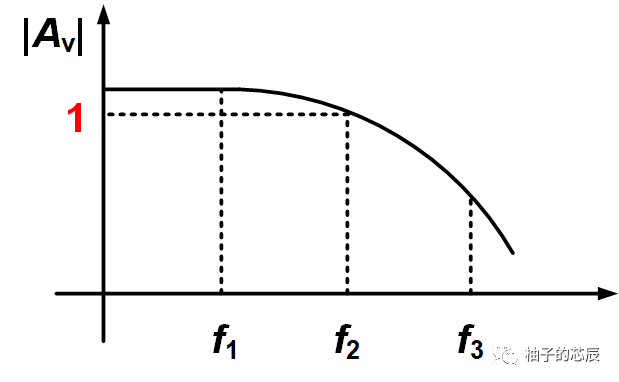
此外,每個陀螺儀傳感器在通過ADC模塊之前都會通過雙極低通濾波器。這樣可以提供足夠的信息,以便使用拉普拉斯變換來開發S域中的傳遞函數表示。第一極(f1)的頻率為404 Hz,第二極(f2) 的頻率為757 Hz。

?
加速度計的單極 (f1)傳遞函數為:

?
這些公式為程序中的數字分析提供了依據,這些程序可管理與“s = jω” 恒等式相關的復數。在MATLAB中,以下的m-腳本將生成幅度(比率,無單位)和相位(度)信息:
Fmax = 9840/2; % one-half of the sample rate
for f = 1:Fmax
w(f) = 2*pi*f;
end
p1 = 404; % pole location = 404Hz
p2 = 757; % pole location = 757Hz
NUM1 = 2*pi*p1;
DEN1 = [1 2*pi*p1];
NUM2 = 2*pi*p2;
DEN2 = [1 2*pi*p2];
H1 = tf(NUM1,DEN1); % transfer function for first pole
H2 = tf(NUM2,DEN2); % transfer function for second pole
H488a = H1 * H2; % transfer function for 2-pole filter
[maga,phasea] = bode(H488,w);
for f = 1:Fmax
Mag488a(f) = maga(1,1,f);
Phase488a(f) = phasea(1,1,f);
end
為快速評估與這些濾波器相關的時間延遲,請注意單極濾波器的相位延遲在?3 dB頻率下等于45°,也就是轉折頻率周期的1/8。在此情況下,加速度計的濾波器的時間延遲大約等于0.38 ms。對于陀螺儀,延遲等于兩級的時間延遲的總和,約為0.47 ms。

?
均值/抽取濾波器級
圖3說明了兩個均值/抽取濾波器級的使用,它們可以降低級的輸出采樣速率,并且提供額外的濾波。在具有有限脈沖響應(FIR)的數字濾波器中,相位延遲等于總抽頭數的一半,除以每個抽頭的采樣速率。在第一個濾波級,采樣速率為9.84 kHz。有四個抽頭,在此種類型的濾波器中,這個數字等于均值數量。相位延遲約為0.2 ms。均值濾波器的幅度響應遵循這種關系。

?
使用MATLAB進行分析時,請使用9.84 kSPS的采樣速率(fs)和4個抽頭(N),以及用于分析模擬濾波器的相同頻率數組(N)。使用相同頻率數組,可以更加簡單地組合每級的結果。請使用以下代碼來分析第一級:
Fmax = 9840/2; % one-half of the sample rate
f = 1:Fmax;
NUM(f) = sin(4*pi*f/9840);
DEN(f) = 4 * sin(pi*f/9840);
for fq = 1:Fmax
Hda(fq) = abs(NUM(fq)/DEN(fq));
end
要分析第二個均值/抽取濾波器,需要事先了解控制系統的采樣速率,但應使用相同的關系。例如,如果控制環路需要接近400 SPS的采樣速率,則第二個濾波器的均值和抽取率將等于6(采樣速率為410 SPS,有四個樣本,因此為9840/[410 × 4] = 6)。使用相同的m-script 腳本代碼可分析幅度響應,有三個例外:(1) 將采樣速率從9480更改為2460;(2) 將兩個位置的“4”更改為“6”;以及 (3) 將FMAX從9840/2更改為2460/2。相位等于總抽頭數的一半,除以采樣速率,約為1.22 ms (3/2460)。
復合響應
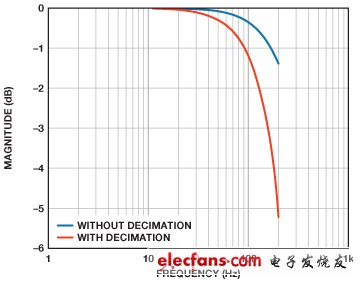
圖4和圖5提供了復合幅度和相位響應,包括陀螺儀的模擬濾波器和兩個抽取濾波器。圖4表示針對數組中的每個頻率,將各級的幅度相乘的結果。圖5表示將每個頻率下的各級的相位貢獻相加的結果。標記“沒有抽取”的坐標圖假定輸出數據速率為2460 SPS,第二個抽取濾波器級有效關閉。標記“有抽取”的坐標圖假定抽取率等于6,最終輸出數據速率為410 SPS。兩個坐標圖說明了響應差異,幫助實現控制環路采樣速率和相應頻率響應的系統級平衡。
?
圖4. 模擬濾波器和第一個抽取濾波器級。

?
圖5. 410-SPS數據速率的復合響應。
可編程FIR濾波器分析
知道模擬濾波器和抽取濾波器的貢獻之后,我們可以評估使用片內抽取濾波器和設計自定義FIR濾波器之間的比較權衡。在圖3所示的ADIS16488中,FIR濾波器包括在IMU中,但有些系統在數字信號處理程序中實施濾波器。FIR濾波器的時域f(n) 以差分方程表示,其中z變換提供了用于頻率分析的分析工具:

?
幸運的是,很多現代程序都包含根據基本關系進行此類分析的特定工具或命令。但在驗證自動評估工具的結果或對FIR設計工具輸出產生直覺的疑問時,了解它們仍然是有用的。MATLAB“fdatool”命令可啟動濾波器分析和設計軟件包,幫助設計和分析系統FIR濾波器實施。
慣性頻率響應測試方法
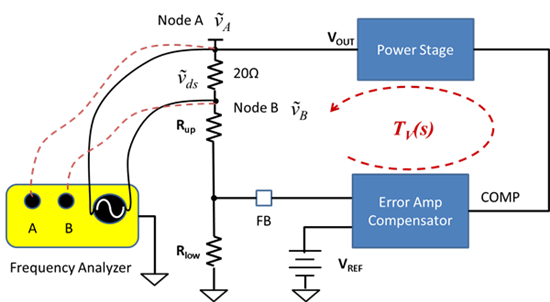
在陀螺儀中測試頻率響應的最直接方法是使用慣性速率表,它能夠引入適當的頻率成分。速率表通常包括可編程伺服電機和光學編碼器,可驗證電機軸上的編程旋轉。這種測試方法的優勢是它應用了實際慣性運動。它的弱點在于它通常不適用于剛開始使用MEMS的工程師。
對于未使用速率表的早期分析驗證,測試目標頻段內的頻譜噪聲可以提供有用的信息。這種簡化方法不需要復雜的測試設備,而只需要與穩定平臺的安全機械連接以及數據收集儀表。但是,它要求機械噪聲具有相對于頻率的“平坦”噪聲幅度。
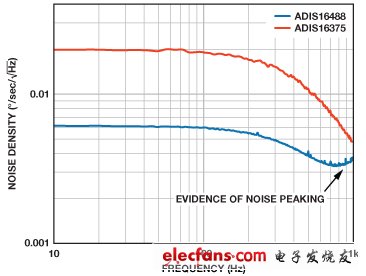
圖6詳細說明了使用相同雙極低通濾波器的兩個例子。第一個例子 (ADIS16375)使用了在有用頻率范圍內具有平坦響應的陀螺儀。第二個例子(ADIS16488)使用在1.2 kHz頻率下具有適中峰化量的陀螺儀,它實際上將–3 dB頻率擴展到大約380 Hz。對于在為控制環路進行建模和仿真的人員而言,了解這種共振行為可能是非常有價值的。在簡單測試中識別這種行為,還有助于解釋在執行更全面系統特征化時噪聲電平高于預期的原因。如果在項目早期了解和識別這些行為,則通常可通過對濾波器極點的調整,對它們進行管理。
測量噪聲密度時,請確保采樣速率至少達到最高目標頻率的兩倍,以滿足奈奎斯特準則。此外,還應提取足夠的數據樣本,以降低測量的不確定性。圖6中的坐標圖源于FFT時間記錄分析,長度為256000個采樣,最大速率為2.46 kSPS。
?
圖6. 噪聲密度比較。
另一種方法使用了陀螺儀的自測功能。自測功能提供了使用電氣信號來模擬傳感器的機械結構的機會,而無需對設備施加外部慣性運動。自測功能迫使模擬對實際運動的響應的傳感器內核中發生變化,從而在電氣輸出上產生相應變化。并非所有產品都提供對此信息的實時訪問,但它可能是一種有用工具,另外制造商或許能夠提供此種類型的頻率-響應測試的數據。在最簡單的方法中,可將自測(模擬對步驟的響應)與分析預期結果進行比較。重復在特定頻率下的自測置位,也是一種研究每個頻率下的傳感器響應幅度的直接方法。以圖7中的兩種不同響應為例。在較低頻率下,陀螺儀輸出類似于方波,每個轉換的瞬態響應除外。瞬態響應符合傳感器信號鏈中的濾波器網絡的“步驟響應”預期。在第二個示例中,自測的頻率足夠高,能夠防止完全建立,因而發生了幅度減小。請注意在本圖底部信號上,藍色和黑點響應之間的幅度差異。有多種方法可以估測這些時間記錄的幅度。離散傅里葉變換(DFT)可將主要頻率成份(自測頻率)與諧波內容隔離開,這可能導致幅度/頻率響應的誤差。

?
圖7. 自測。
結論
向高帶寬IMU發展的趨勢為反饋穩定系統的設計提供了顯著優勢。高帶寬使得多傳感器系統能夠實現更好的時序對齊和相位裕量管理。濾波電容的值和溫度響應的變化范圍可能非常廣,可能導致極點頻率的成比例變化。由于相位延遲取決于極點位置,因此了解和管理極點位置非常重要。例如,當反饋傳感器的截止頻率比控制器的單位增益反饋高兩倍時,則會為環路響應增加大約22.3°的相位延遲。如果截止頻率降低20%,則相位延遲增加大約5.6°。提高單位增益帶寬中的截止頻率的比率,可將這些影響減小4倍。
要了解IMU的帶寬及其在系統穩定性中的角色,應該使用分析、建模、測試數據以及這些因素的迭代。首先要量化可用信息,做出假設以彌補所有漏洞,然后制定計劃來優化這些假設。
 電子發燒友App
電子發燒友App










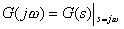
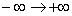
















評論