原信號的不同類型,傅里葉變換可以分為四種類別: (1)非周期性連續(xù)信號傅里葉變換 (2)周期性連續(xù)信號傅里葉級數(shù) (3)非周期性離散信號離散時域傅里葉變換 (4)周期性離散信號離散傅里葉變換 快速傅里葉變換(FFT),是利用計算機計算離散傅里葉
2020-11-09 16:52:40 12478
12478 
快速傅里葉變換 (Fast Fourier Transform,F(xiàn)FT), 即利用計算機計算離散傅里葉變換(DFT)的高效、快速計算方法的統(tǒng)稱,簡稱FFT。
2023-07-20 16:46:23 2011
2011 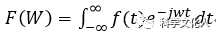
傳統(tǒng)傅里葉變換的分析方法大家已經(jīng)非常熟悉了,特別是快速傅里葉變換(FFT)的高效實現(xiàn)給數(shù)字信號處理技術(shù)的實時應(yīng)用創(chuàng)造了條件,從而加速了數(shù)字信號處理技術(shù)的發(fā)展。
2024-01-07 09:46:20 643
643 
傅里葉變換在物理學、數(shù)論、組合數(shù)學、信號處理、概率論、統(tǒng)計學、密碼學、聲學、光學、海洋學、結(jié)構(gòu)動力學等領(lǐng)域都有著廣泛的應(yīng)用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量
2019-06-28 06:52:47
以前知道:傅里葉級數(shù)可以看做是時域中信號周期且連續(xù),或者頻域中信號非周期且離散那么傅里葉變換是把時域中的非周期連續(xù)信號,轉(zhuǎn)換成了頻域中的非周期什么性質(zhì)的信號?這個性質(zhì)是指是連續(xù)的還是離散的?謝謝回答!
2017-02-13 11:26:03
快速傅里葉變換,越來越看著重要了,一定要好好學習
2012-06-04 15:47:52
快速傅里葉變換C語言實現(xiàn) 模擬采樣進行頻譜分析FFT是DFT的快速算法用于分析確定信號(時間連續(xù)可積信號、不一定是周期信號)的頻率(或相位、此處不研究相位)成分,且傅里葉變換對應(yīng)的ω\omega
2021-07-20 06:01:26
快速傅里葉變換FFT算法及其應(yīng)用
2020-05-28 09:13:10
C語言實現(xiàn)FFT(快速傅里葉變換)
2013-10-25 21:33:41
第24章 DSP變換運算-傅里葉變換本章節(jié)開始進入此教程最重要的知識點之一傅里葉變換。關(guān)于傅里葉變換,本章主要是把傅里葉相關(guān)的基礎(chǔ)知識進行必要的介紹,沒有這些基礎(chǔ)知識的話,后面學習FFT(快速
2021-08-03 06:14:23
快速傅里葉變換FFT
2015-07-15 17:52:28
內(nèi)容簡介 本書就數(shù)字信號處理的基本理論、算法及MATLAB實現(xiàn)進行系統(tǒng)的論述。全書共7章,前兩章簡要介紹了離散時間信號與系統(tǒng)及Z變換,第3、4章討論離散傅里葉變換及快速算法,第5~7章介紹數(shù)字濾波器
2011-07-09 09:31:26
本帖分為兩個部分,一個是用CCS的圖形工具,畫出仿真信號的時域圖,另一部分是相對這個信號進行傅里葉變換的時候遇到的問題。(當然這里面的算法中的命名規(guī)則、C的書寫方式都不符合C標準,而且現(xiàn)在剛開始還只
2015-10-28 21:34:46
的基礎(chǔ)知識進行必要的介紹,沒有這些基礎(chǔ)知識的話,后面學習FFT(快速傅里葉變換)時會比較困難。本章節(jié)的內(nèi)容主要來自百度百科,wiki百科以及網(wǎng)絡(luò)和書籍中整理的一些資料。 23.1 傅里葉人物簡介 23.2 傅里葉變換概念 23.3 傅里葉的特殊形式 23.4 傅里葉變換相關(guān)知識 23.5 總結(jié)
2015-06-25 09:58:09
對信號進行處理。因此至DFT被發(fā)現(xiàn)以來,在很長的一段時間內(nèi)都不能被應(yīng)用到實際的工程項目中,直到一種快速的離散傅立葉計算方法——FFT,被發(fā)現(xiàn),離散是傅立葉變換才在實際的工程中得到廣泛應(yīng)用。需要
2015-06-26 10:40:16
做是沒有意義的,在傅里葉變換和傅里葉逆變換之間有一個濾波的過程。將不要的頻率分量給濾除掉,然后再做逆變換,就得到了想要的信號。比如信號中摻雜著噪聲信號,可以通過濾波器將噪聲信號的頻率給去除,再做傅里葉
2024-03-12 16:06:54
二傅里葉變換是什么?三傅里葉變換的意義是什么?如何求傅里葉變換?
2021-05-08 09:23:56
('|P1(f)|')對原信號進行傅里葉變換Y = fft(S);P2 = abs(Y/L);P1 = P2(1:L/2+1);P1(2:end-1) = 2*P1(2:end-1);plot(f,P1
2019-03-22 09:45:34
有關(guān)這些處理器的更多信息和支持資源。CMSIS-DSP在行業(yè)中得到了廣泛使用,并能夠通過各種第三方工具優(yōu)化C代碼生成。例程所使用的是DSP開發(fā)包中的TransformFunctions實數(shù)快速傅里葉變換
2022-06-12 19:17:26
分享C語言的快速傅里葉變換源代碼,本人是新手,希望大家多多指點,調(diào)錯誤
2015-05-07 19:17:13
周期信號的傅里葉變換.ppt
2017-10-03 23:06:29
進行傅里葉變換。 短時傅里葉變換具有明顯的物理意義,它可以看作是信號x(n)在“分析時間”n附近的“局部頻譜”,當n變化時,得到信號頻率隨時間n變化的規(guī)律。可以看出,DSTFT將時域和頻域組合
2009-10-23 10:41:14
學習傅里葉變換需要面對大量的數(shù)學公式,數(shù)學功底較差的同學聽到傅里葉變換就頭疼。事實上,許多數(shù)學功底好的數(shù)字信號處理專業(yè)的同學也不一定理解傅里葉變換的真實含義,不能做到學以致用!事實上,傅里葉變換
2019-06-28 07:31:30
抽樣信號的傅里葉變換.ppt
2017-10-03 23:15:08
抽樣信號的傅里葉變換.zip
2017-10-04 11:49:07
實際電路中,放大電路放大一個電源噪聲信號自激,在用Multisim仿真時該怎么設(shè)置?
2016-06-20 11:00:49
一、問題來源??在討論如下無窮電阻網(wǎng)絡(luò)兩個相鄰節(jié)點之間的電阻。特別有意思的是,文中還是用了離散傅里葉變換(DFT)給出了另外一種求解方式。這不禁讓人們好奇:在這樣的電阻網(wǎng)絡(luò)分析中,離散傅里葉變換
2022-08-19 15:59:46
DFT被發(fā)現(xiàn)以來,在很長的一段時間內(nèi)都不能被應(yīng)用到實際的工程項目中,直到一種快速的離散傅立葉計算方法——FFT,被發(fā)現(xiàn),離散是傅立葉變換才在實際的工程中得到廣泛應(yīng)用。需要強調(diào)的是,F(xiàn)FT并不是一種
2016-09-27 08:09:05
本帖最后由 richthoffen 于 2019-7-19 16:41 編輯
詳解快速傅里葉變換FFT算法
2019-07-18 08:07:33
詳解快速傅里葉變換FFT算法
2020-03-28 11:48:16
詳解快速傅里葉變換FFT算法
2020-05-25 09:31:30
詳解快速傅里葉變換FFT算法
2021-03-05 11:07:32
各位大佬,小弟新手,求教調(diào)用正弦信號發(fā)射器產(chǎn)生了一個正弦波,現(xiàn)在要疊加一個噪聲信號在里面,嚴重后面的濾波功能。1,噪聲信號的產(chǎn)生不會弄2,將噪聲信號疊加進去不會弄
2019-08-28 20:05:19
`采集的環(huán)境中會有尖峰噪聲出現(xiàn),不知道用什么濾波器可以去掉尖峰?第一個問題:之前用的是巴特沃斯低通濾波器,先用快速傅里葉變換FFT,測得信號頻率之后,將噪聲頻率值輸入到低通截止頻率進行濾波,但是
2019-03-04 16:47:31
怎么用labview對一個連續(xù)信號(連續(xù)變化的加速度值)進行傅里葉變換?是不是需要先濾波,然后加窗,然后FFT?不知道是不是這樣,具體該怎么實現(xiàn)呢?
2019-05-03 20:20:00
從本章開始由時域轉(zhuǎn)入變換域分析,首先討論傅里葉變換。傅里葉變換是在傅里葉級數(shù)正交函數(shù)展開的基礎(chǔ)上發(fā)展而產(chǎn)生的,這方面的問題也稱為傅里葉分析(頻域分析)。將信號
2008-08-05 11:49:37 50
50 離散傅里葉變換及其快速算法離散傅里葉變換 (Discrete Fourier Transform,DFT)是時間函數(shù)是離散的,而且頻譜函數(shù)也是離散的變換。3. 1 討論周期序列的 傅里葉級數(shù)及其性質(zhì)。
2008-10-30 12:54:54 33
33 從傅里葉變換、短時傅里葉變換到小波變換的思想發(fā)展過程中分析了小波變換發(fā)展的必然性和重要性,并通過MATLAB仿真工具比較了三種變換在信號處理中的應(yīng)用。實驗結(jié)果表明,
2009-02-27 15:33:50 22
22 什么是傅里葉變換
傅里葉變換(Transformée de Fourier)是一種積分變換。
因其基本思想首先
2007-11-29 12:46:55 8536
8536 
非周期信號的傅里葉變換
前面已討論了周期非正弦信號的傅里葉級數(shù)展開,下面來分析非周期信號的傅里葉變換。當周期
2009-07-27 10:23:30 8695
8695 對于高頻信號和高頻噪聲干擾相混疊的信號,采用小波變換去除噪聲可以避免用傅里葉變換去噪帶來的信號折損。對于噪聲頻率固定的平穩(wěn)信號,在對信號進行傅里葉變換后使用濾波器
2011-03-18 16:47:24 426
426 為了減小匹配傅里葉變換分析的計算量,提出了一種基于快速傅里葉變換的快速算法。根據(jù)匹配傅里葉變換的分解將積分形式轉(zhuǎn)化為離散形式,推導出快速算法表達式。該算法與直接的
2013-07-26 11:48:36 77
77 matlab關(guān)于傅里葉變換的一些實現(xiàn)方法。
2016-02-23 18:21:54 0
0 有關(guān)傅里葉變換的matlab教程,簡單明了。
2016-02-23 18:22:10 0
0 【檢測技術(shù)】 快速傅里葉變換,測控技術(shù)儀器必備課程,喜歡學習的朋友可以下載學習學習。
2016-11-18 16:53:48 0
0 數(shù)字信號處理第4章-快速傅里葉變換(FFT)
2016-12-28 14:23:30 0
0 基于MATLAB濾波算法對圖像噪聲信號處理的實現(xiàn)_肖玉芝
2017-03-18 08:58:38 7
7 快速傅里葉變換 (fast Fourier transform),即利用計算機計算離散傅里葉變換(DFT)的高效、快速計算方法的統(tǒng)稱,簡稱FFT。快速傅里葉變換是1965年由J.W.
2017-11-27 16:23:01 1494
1494 抽樣信號的傅里葉變換
2017-12-06 14:36:01 0
0 非周期信號的頻譜分析─傅里葉變換
2017-12-06 14:30:13 0
0 小波變換與傅里葉變換有什么區(qū)別嗎?小波變換與傅里葉變換哪個好?我們通過小波變換與傅里葉變換的詳細解讀、小波變換與傅里葉變換的區(qū)別、傅里葉變換缺點方面來解析。
2018-01-13 11:02:22 14344
14344 
傅里葉變換在物理學、電子類學科、數(shù)論、組合數(shù)學、信號處理、概率論、統(tǒng)計學、密碼學、聲學、光學、海洋學、結(jié)構(gòu)動力學等領(lǐng)域都有著廣泛的應(yīng)用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值譜——顯示與頻率對應(yīng)的幅值大小)。
2018-01-28 11:35:47 93804
93804 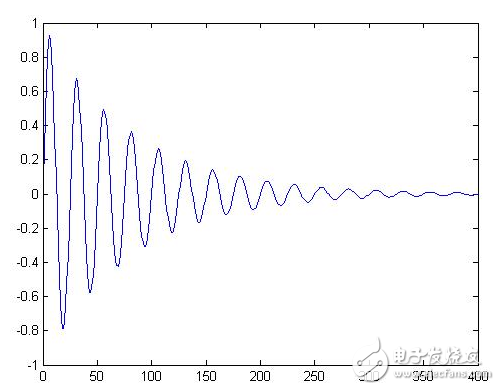
主要內(nèi)容:
1.正弦信號的傅里葉變換
2.一般周期信號的傅里葉變換
3.如何由F0(ω)求F(nω1)
4.單位沖激序列的傅氏變換
5.周期矩形脈沖序列的傅氏變換
2018-03-05 10:59:05 2
2 快速傅里葉變換是一種有效的算法類的數(shù)字計算N點傅里葉變換(DFT)。
2018-04-12 09:52:24 2
2 傅里葉變換是數(shù)字信號處理領(lǐng)城種很重要的算法。傅里葉表明:任何連續(xù)測量的時序或信號,都可以表示為不同頻率的正弦波信號的無限疊加。而根據(jù)該原理的傅里葉變換算法利用直接測量到的原始信號,以累加方式來計算
2019-04-30 08:00:00 2
2 FFT為Fast Fourier Transformation,即快速傅里葉變換,本項目中,F(xiàn)FT的目標是識別頻率為形如式的一個正弦信號:
2019-08-06 08:00:00 56
56 周期矩陣脈沖信號傅里葉變換問題求解
2021-06-26 14:49:06 0
0 快速傅里葉變換 (Fast Fourier Transform,F(xiàn)FT), 即利用計算機計算離散傅里葉變換(DFT)的高效、快速計算方法的統(tǒng)稱,簡稱FFT。DFT是實現(xiàn)了從頻域(頻域分析往往比時域
2022-07-22 10:17:25 1225
1225 信噪比(SNR)是信號與噪聲的比率,它是衡量通信或模擬系統(tǒng)性能的重要指標之一,與傅里葉變換更是有千絲萬縷的聯(lián)系。
2022-11-03 10:36:19 4542
4542 
傅氏變換分析是信號分析中很重要的方法,借助matlab可以很方便的對各類信號進行傅氏頻域分析。本文介紹了集中離散的傅氏變換以及matlab實現(xiàn)方法。
2023-07-19 10:10:49 1265
1265 
本文主要給定一小段音頻,通過短時傅里葉變換和小波變換制作時頻圖。音頻的采樣率為44100
2023-07-19 17:44:25 1069
1069 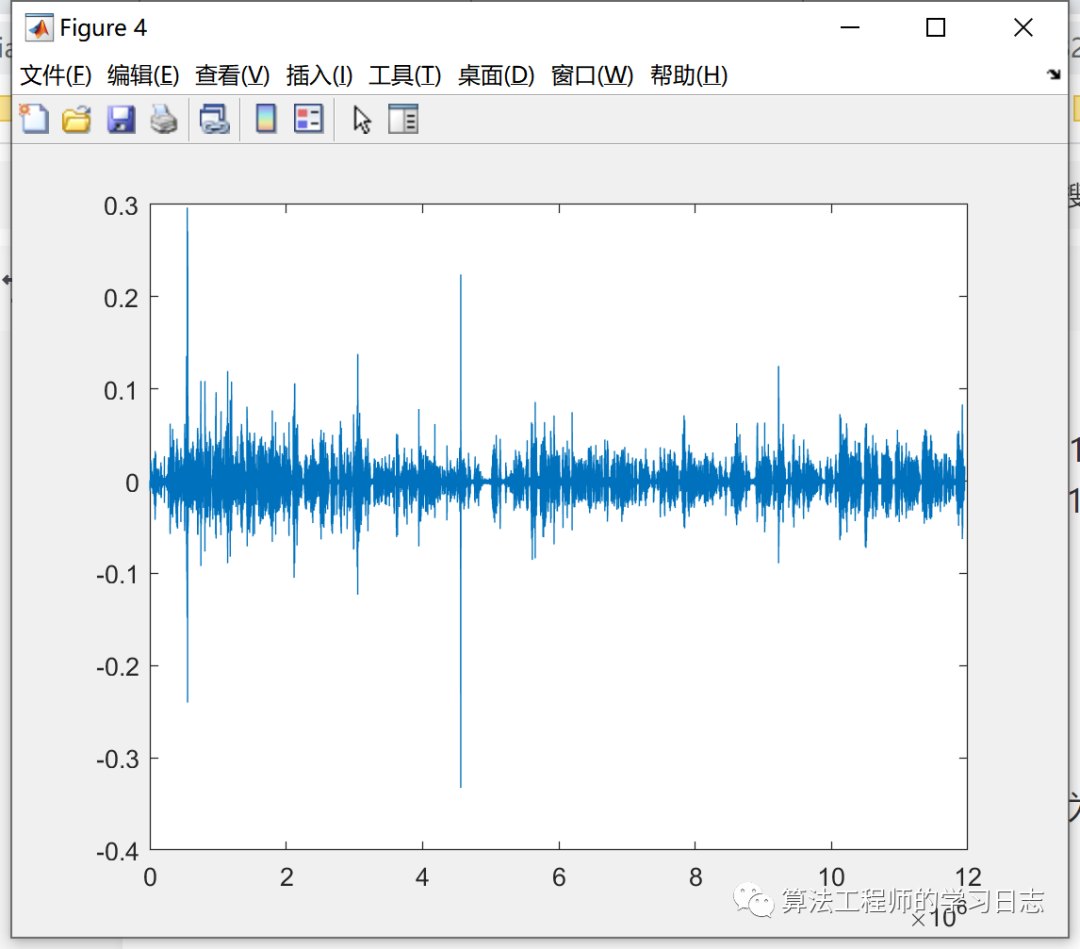
傅里葉變換是將按時間或空間采樣的信號與按頻率采樣的相同信號進行關(guān)聯(lián)的數(shù)學公式。
2023-07-19 17:47:30 3511
3511 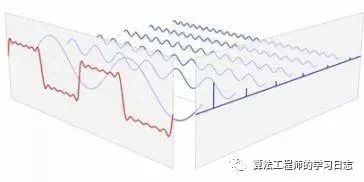
信號在頻域能夠呈現(xiàn)出時域不易發(fā)現(xiàn)的性質(zhì)和規(guī)律,傅里葉變換是將信號從時域變換到頻域,便于在頻域?qū)?b class="flag-6" style="color: red">信號的特性進行分析。
2023-07-20 17:33:17 2214
2214 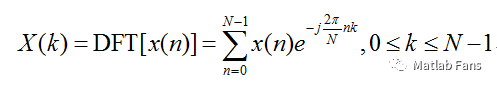
雖然周期信號不滿足絕對可積條件,但認為沖激函數(shù)有意義下絕對可積稱為不必要的限制
頻移特性——余弦信號(周期)的傅里葉變換——導出其余信號的頻譜函數(shù)
2023-08-09 15:06:46 573
573 
在計算傅里葉變換之前對信號去趨勢是一種常見的做法,特別是在處理時間序列時。在這篇文章中,我將從數(shù)學和視覺上展示信號去趨勢是如何影響傅里葉變換的。
2023-08-16 15:26:23 492
492 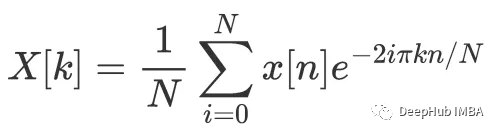
傅里葉變換的意義和理解 傅里葉變換是一種將一個信號在頻域中進行分解的數(shù)學工具,它將一個信號分解為不同頻率的正弦和余弦波的疊加。傅里葉變換的基本概念源于法國數(shù)學家約瑟夫·傅里葉,而其在現(xiàn)代通信、圖像
2023-09-07 16:08:42 5376
5376 傅里葉變換對信號處理的意義? 傅里葉變換是一種基本的數(shù)學工具,它經(jīng)常用于信號處理中。在這篇文章中,我們將探討傅里葉變換的意義和應(yīng)用。 傅里葉變換的定義是將一個函數(shù)表示為它的頻域表示。傅里葉變換
2023-09-07 16:14:33 918
918 傅里葉變換十大公式 傅里葉變換的十大性質(zhì)? 傅里葉變換是一種重要的數(shù)學工具,在許多領(lǐng)域中都有廣泛的應(yīng)用。傅里葉變換可以將一個時域信號轉(zhuǎn)化為頻域信號,分析不同頻率成分在信號中的占比情況。由于傅里葉變換
2023-09-07 16:14:36 8654
8654 傅里葉變換的目的和意義 傅里葉變換幾何意義? 傅里葉變換是一種重要的數(shù)學工具和分析方法,它在信號處理、圖像處理、音頻處理等領(lǐng)域有著廣泛的應(yīng)用。它的目的是將一個時域信號轉(zhuǎn)換為頻域信號,從而更好地理
2023-09-07 16:14:39 1475
1475 傅里葉變換基本性質(zhì) 傅里葉變換本質(zhì) 傅里葉變換的應(yīng)用 傅里葉變換是現(xiàn)代數(shù)學、物理學、工程學等領(lǐng)域中非常重要的一種數(shù)學工具和基本理論。在信號處理、圖像處理、通信技術(shù)、音樂分析、光學、醫(yī)學、天氣預(yù)報
2023-09-07 16:18:49 5501
5501 對圖像進行傅里葉變換的意義 傅里葉變換是一種將一個信號分解成其頻率分量的方法,它在信號處理、圖像處理、電信領(lǐng)域、計算機視覺領(lǐng)域等方面都有著廣泛的應(yīng)用。在圖像處理領(lǐng)域中,傅里葉變換可以將圖像從空間
2023-09-07 16:18:56 1507
1507 傅里葉變換的時移特性 傅里葉變換是一種非常重要的數(shù)學工具,可以將任何周期性信號或非周期性信號進行頻域分析,從而在通信、電子工程等領(lǐng)域中得到廣泛應(yīng)用。傅里葉變換能夠?qū)?b class="flag-6" style="color: red">信號從時域(時間域)轉(zhuǎn)換到頻域
2023-09-07 16:23:19 2306
2306 短時傅里葉變換特點 短時傅里葉變換的意義? 短時傅里葉變換(Short-time Fourier Transform, STFT)是一種時頻分析方法,它把信號在時間和頻率上進行分解,可以對信號的短時
2023-09-07 16:23:22 1423
1423 、通信工程、電子工程等領(lǐng)域中廣泛使用的重要工具。 在傅里葉變換的應(yīng)用中,經(jīng)常需要進行頻移操作。頻移是指將信號在頻域上平移一定的頻率。頻移可以改變信號在頻域上的特性,例如移動頻率可以改變信號的中心頻率和帶寬。傅
2023-09-07 16:29:36 1650
1650 傅里葉變換的時移特性和頻移特性 傅里葉變換是一種將時域函數(shù)轉(zhuǎn)換為頻域函數(shù)的數(shù)學工具,是信號處理領(lǐng)域中的重要工具之一。在信號處理中,時移和頻移是常見的操作,傅里葉變換的時移和頻移特性對于處理信號非常
2023-09-07 16:29:38 4553
4553 傅氏變換和傅里葉變換的區(qū)別聯(lián)系 傅氏變換和傅里葉變換是信號處理中常用的兩種變換方法,它們有著不同的作用和特點。傅氏變換主要應(yīng)用于連續(xù)時間信號的頻域分析,而傅里葉變換則主要用于離散時間信號的頻域分析
2023-09-07 16:35:05 865
865 傅里葉變換拉普拉斯變換和z變換的區(qū)別聯(lián)系 傅里葉變換、拉普拉斯變換和z變換是信號處理中重要的數(shù)學工具。傅里葉變換用于將一個連續(xù)時間信號轉(zhuǎn)換為頻域表示;拉普拉斯變換則用于將一個連續(xù)時間信號轉(zhuǎn)換為復(fù)平面
2023-09-07 16:38:58 1418
1418 傅里葉變換和傅里葉逆變換的關(guān)系? 傅里葉變換和傅里葉逆變換是信號處理領(lǐng)域中極具重要性的數(shù)學工具,它們被廣泛應(yīng)用于很多領(lǐng)域,例如音頻、圖像處理、通信等。 傅里葉變換是將一個信號在時域(即時間或空間
2023-09-07 16:43:47 3087
3087 和洞察力。這種變換在信號處理、圖像處理、量子力學等領(lǐng)域有廣泛的應(yīng)用。現(xiàn)在我們來詳細了解傅里葉變換的公式。 一、連續(xù)信號的傅里葉變換公式 傅里葉變換最初是用于連續(xù)時間信號的, 我們可以看到 X(ω) 是通過對時域上信號進行積
2023-09-07 16:47:46 4301
4301 傅里葉變換的實現(xiàn)方法? 傅里葉變換是一種將信號在時間域和頻率域之間相互轉(zhuǎn)換的數(shù)學工具。它的實現(xiàn)方法有很多種,其中最常見的是離散傅里葉變換(DFT)和快速傅里葉變換(FFT)。 離散傅里葉變換是一種
2023-09-07 16:47:52 575
575 傅里葉變換和反變換公式? 傅里葉變換和反變換在信號處理領(lǐng)域中被廣泛應(yīng)用。傅里葉變換是將一個時域信號轉(zhuǎn)換為頻域信號的過程,而傅里葉反變換則是將一個頻域信號轉(zhuǎn)換為時域信號的過程。這篇文章將詳細講解
2023-09-07 16:53:04 9130
9130 使得分析和處理變得更加簡單。在本文中,我們將詳細解釋傅里葉變換的公式,以幫助讀者更好地理解和應(yīng)用傅里葉變換。 傅里葉變換的基本理論 傅里葉變換是一種將時域上的信號轉(zhuǎn)換到頻域的技術(shù)。在時域中,信號是按照時間變化的,
2023-09-07 16:53:06 2631
2631 為什么有四種形式的傅里葉變換? 傅里葉變換是一種十分重要的數(shù)學工具,它可以將函數(shù)從時域(即時間域)轉(zhuǎn)換到頻域,從而能夠幫助人們更好地理解信號的特性。在傅里葉變換的研究過程中,出現(xiàn)了幾種不同的變形方式
2023-09-07 17:04:04 841
841 小波變換與傅里葉變換的區(qū)別和聯(lián)系? 1. 傅里葉變換和小波變換的定義 傅里葉變換(Fourier Transform,簡稱FT)是一種將信號在時域上的函數(shù)轉(zhuǎn)變?yōu)轭l域上的函數(shù)的方法,對于連續(xù)時間信號
2023-09-07 17:04:07 1640
1640 如何由傅里葉變換推出傅里葉反變換? 傅里葉變換和傅里葉反變換是信號處理和通信領(lǐng)域中的兩個重要概念,是數(shù)字信號和連續(xù)信號的重要數(shù)學分析方法之一。傅里葉變換可以將時間域信號轉(zhuǎn)化為頻率域信號
2023-09-07 17:04:09 1267
1267 短時傅里葉變換和小波變換差別 短時傅里葉變換(short-time Fourier transform,STFT)和小波變換(wavelet transform)是兩種常見的信號處理技術(shù),它們在頻域
2023-09-07 17:04:12 1551
1551 傅里葉變換和離散傅里葉變換的關(guān)系 傅里葉變換(Fourier Transform)是一種將時間域(或空間域)的信號轉(zhuǎn)換為頻率域(或波數(shù)域)的信號的數(shù)學工具。而離散傅里葉變換(Discrete
2023-09-07 17:04:15 1423
1423 電子發(fā)燒友網(wǎng)站提供《基于快速傅里葉變換的并行碼相位快速捕獲技術(shù)研究.pdf》資料免費下載
2023-10-24 11:28:22 0
0 電子發(fā)燒友網(wǎng)站提供《基于快速傅里葉變換的快速算法.pdf》資料免費下載
2023-11-06 10:25:41 0
0 形式,如連續(xù)傅里葉變換和離散傅里葉變換。最初傅里葉分析是作為熱過程的解析分析的工具被提出的。 傅里葉變換的意義主要體現(xiàn)在以下幾個方面: 1. 頻譜分析:傅里葉變換可以將一個信號分解成不同頻率的分量。通過分析每個頻率分量的振幅
2023-11-30 15:32:49 732
732 Fourier)于19世紀提出的。傅里葉變換在信號處理和物理學等領(lǐng)域有廣泛的應(yīng)用,可以用來分析和處理各種波動現(xiàn)象。 傅里葉變換的應(yīng)用非常廣泛,在信號處理領(lǐng)域幾乎涵蓋了所有的應(yīng)用場景。其中一個重要的應(yīng)用是信號濾波。通過傅里葉變換,我們可以將一個信號轉(zhuǎn)換到頻域中,并利用頻域
2024-02-02 10:36:58 273
273
 電子發(fā)燒友App
電子發(fā)燒友App





















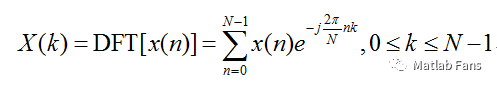

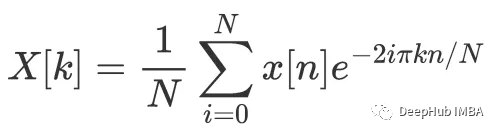










評論