毫無疑問,過去兩年中,機器學習和人工智能的普及度得到了大幅提升。
如果你想學習機器算法,要從何下手呢?以我為例,我是在哥本哈根留學期間,學習AI課程入門的。我們用的教科書是一本AI經典:《Peter Norvig’s Artificial Intelligence?—?A Modern Approach》。最近我在繼續學習這些,包括在舊金山聽了幾個關于深度學習的技術演講,參加機器學習大會上。六月份,我注冊了Udacity的Intro to Machine Learning的在線課程,近期已經完成了。這篇文章,我想分享一些我所學到的、最常見的機器學習算法。
我從這個課程中學到了很多,并決定繼續學習這一專業內容。不久前,我在舊金山聽了幾個關于深度學習、神經網絡、數據架構方面的技術演講,包括在一個機器學習大會上和很多領域知名專家一起。最重要的是,我六月份注冊了Udacity 的機器學習入門的在線課程,近期已經完成了。這篇文章,我想分享一些我所學到的、最常見的機器學習算法。
機器學習算法可以分為三個大類——有監督學習、無監督學習和強化學習。
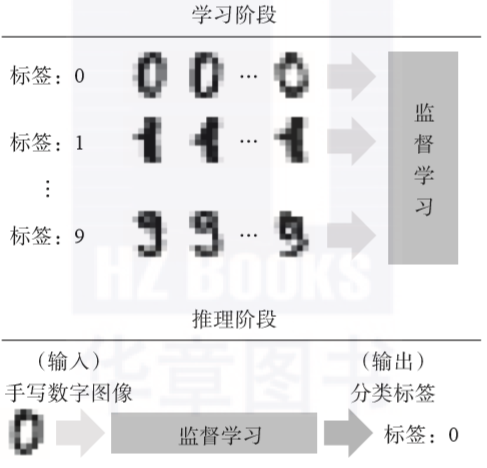
有監督學習,對訓練有標簽的數據有用,但是對于其他沒有標簽的數據,則需要預估。
無監督學習,用于對無標簽的數據集(數據沒有預處理)的處理,需要發掘其內在關系的時候。
強化學習,介于兩者之間,雖然沒有精準的標簽或者錯誤信息,但是對于每個可預測的步驟或者行為,會有某種形式的反饋。
由于我上的是入門課程,我并沒有學習強化學習,但是下面10個有監督和無監督學習算法已經足以讓你對機器學習產生興趣。
監督學習
1.決策樹 (Decision Trees)
決策樹是一個決策支持工具,它用樹形的圖或者模型表示決策及其可能的后果,包括隨機事件的影響、資源消耗、以及用途。請看下圖,隨意感受一下決策樹長這樣的:
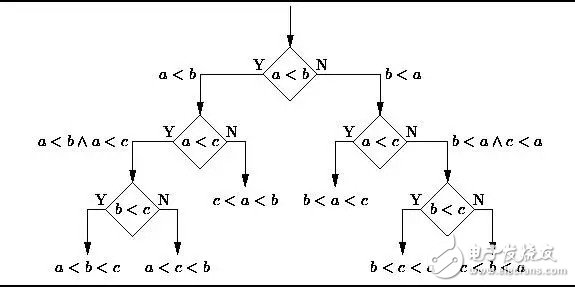
從商業角度看,決策樹就是用最少的Yes/No問題,盡可能地做出一個正確的決策。它讓我們通過一種結構化、系統化的方式解決問題,得到一個有邏輯的結論。
2.樸素貝葉斯分類(Naive Bayes Classification)
樸素貝葉斯分類器是一類簡單概率分類器,它基于把貝葉斯定理運用在特征之間關系的強獨立性假設上。下圖是貝葉斯公式——P(A|B)表示后驗概率,P(B|A)表示似然度,P(A)表示類別的先驗概率(class prior probability),P(B)表示做出預測的先驗概率(predictor prior probability)。

現實生活中的應用例子:
一封電子郵件是否是垃圾郵件
一篇文章應該分到科技、政治,還是體育類
一段文字表達的是積極的情緒還是消極的情緒?
人臉識別
3.普通最小二乘回歸(Ordinary Least Squares Regression)
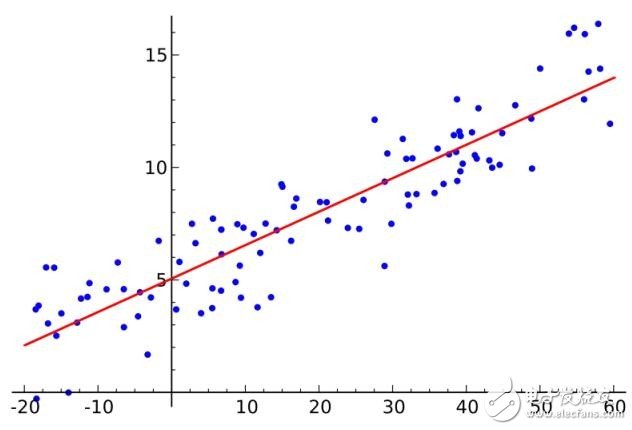
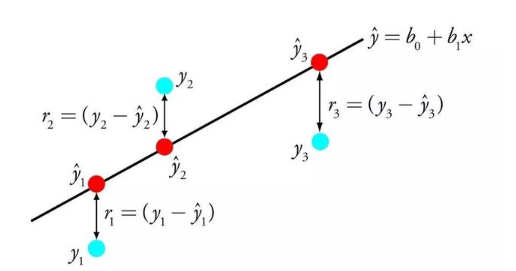
如果你學過統計學,你可能聽過線性回歸。至少最小二乘是一種進行線性回歸的方法。你可以認為線性回歸就是讓一條直線用最適合的姿勢穿過一組點。有很多方法可以這樣做,普通最小二乘法就像這樣——你可以畫一條線,測量每個點到這條線的距離,然后加起來。最好的線應該是所有距離加起來最小的那根。
線性法表示你去建模線性模型,而最小二乘法可以最小化該線性模型的誤差。
4.邏輯回歸(Logistic Regression)
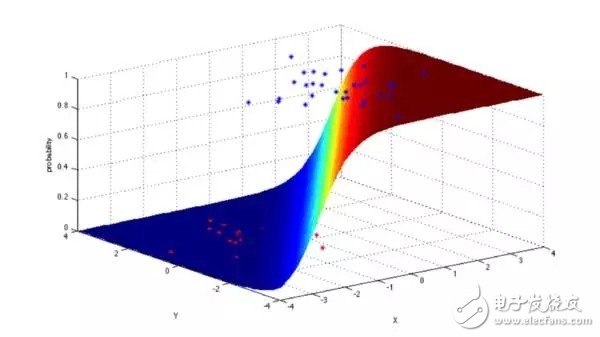
邏輯回歸是一種非常強大的統計方法,可以把有一個或者多個解釋變量的數據,建立為二項式類型的模型,通過用累積邏輯分布的邏輯函數估計概率,測量分類因變量和一個或多個獨立變量之間的關系。
通常,回歸在現實生活中的用途如下:
信用評估
測量市場營銷的成功度
預測某個產品的收益
特定的某天是否會發生地震
5.支持向量機(Support Vector Machines)

SVM是一種二分算法。假設在N維空間,有一組點,包含兩種類型,SVM生成a(N-1) 維的超平面,把這些點分成兩組。比如你有一些點在紙上面,這些點是線性分離的。SVM會找到一個直線,把這些點分成兩類,并且會盡可能遠離這些點。
從規模看來,SVM(包括適當調整過的)解決的一些特大的問題有:廣告、人類基因剪接位點識別、基于圖片的性別檢測、大規模圖片分類…
6.集成方法(Ensemble Methods)
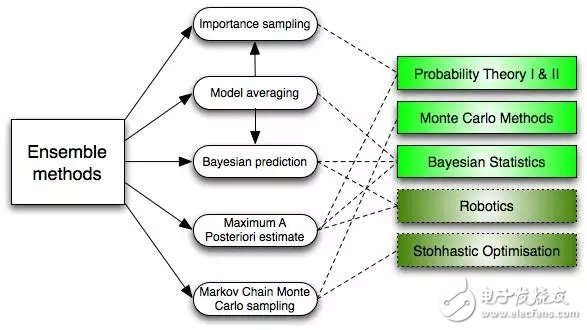
集成方法吸納了很多算法,構建一個分類器集合,然后給它們的預測帶權重的進行投票,從而進行分類。最初的集成方法是貝葉斯平均法(Bayesian averaging),但是最近的算法集還包括了糾錯輸出編碼(error-correcting output coding) ,bagging和boosting
那么集成方法如何工作的?為什么它們比單獨的模型更好?
它們均衡了偏差:就像如果你均衡了大量的傾向民主黨的投票和大量傾向共和黨的投票,你總會得到一個不那么偏頗的結果。
它們降低了方差:集合大量模型的參考結果,噪音會小于單個模型的單個結果。在金融上,這叫投資分散原則(diversification)——一個混搭很多種股票的投資組合,比單獨的股票更少變故。
它們不太可能過度擬合:如果你有單獨的模型不是完全擬合,你結合每個簡單方法建模,就不會發生過度擬合(over-fitting)
無監督學習
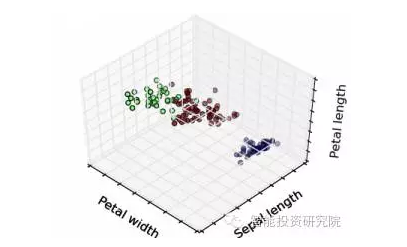
7. 聚類算法(Clustering Algorithms)
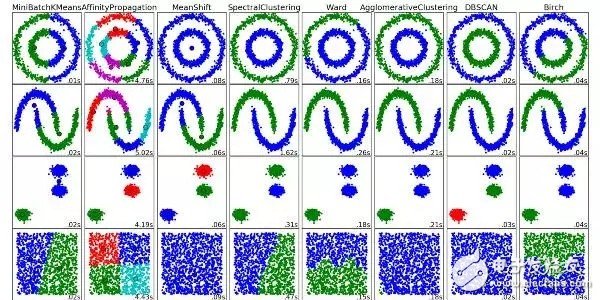
聚類就是把一組對象分組化的任務,使得在同一組的對象比起其它組的對象,它們彼此更加相似。
每種聚類算法都不同,下面是其中一些:
基于圖心(Centroid)的算法
基于連接的算法
基于密集度的算法
概率論
降維
神經網絡 / 深度學習
8.主成分分析(Principal Component Analysis)
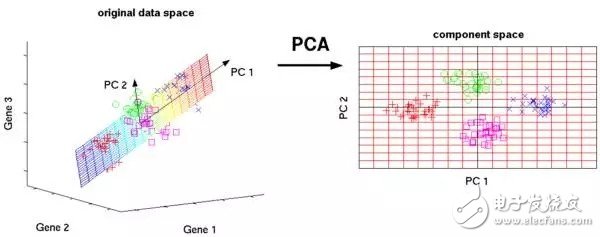
PCA是一種統計過程,它通過正交變換把一組可能相關聯的變量觀察,轉換成一組線性非相關的變量的值,這些非相關的變量就是主成分。
PCA的應用包括壓縮、簡化數據使之易于學習,可視化。需要注意的是,當決定是否用PCA的時候,領域知識特別重要。它不適用于噪音多的數據(所有成分的方差要很高才行)
9.奇異值分解(Singular Value Decomposition)
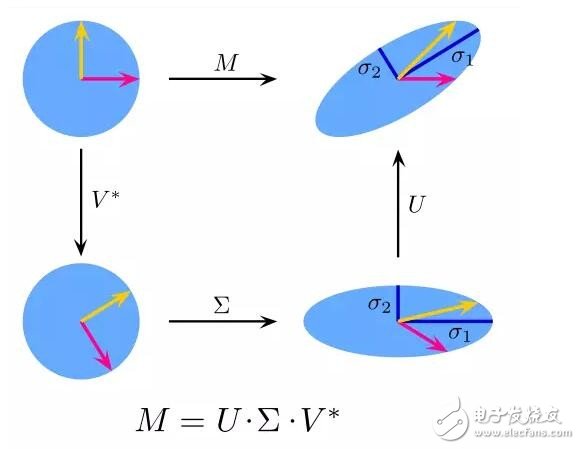
線性代數中,SVD是對一個特別復雜的矩陣做因式分解。比如一個m*n的矩陣M,存在一個分解如M = UΣV,其中U和V是酉矩陣,Σ是一個對角矩陣。
PCA其實是種簡單的SVD。在計算機圖形領域,第一個臉部識別算法就用了PCA和SVD,用特征臉(eigenfaces)的線性結合表達臉部圖像,然后降維,用簡單的方法把臉部和人匹配起來。盡管如今的方法更加復雜,依然有很多是依靠類似這樣的技術。
10.獨立成分分析(Independent Component Analysis)
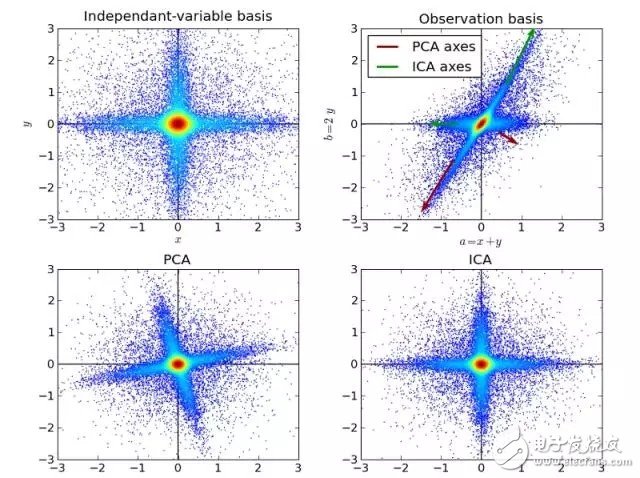
ICA 是一種統計技術。它發掘隨機變量、測量數據或者信號的集合中隱含的因素。ICA定義了一種通用模型,用于觀測到的多變量數據,通常是一個巨大的樣本數據庫。在這一模型中,假設數據變量是一些未知的、潛在的變量的線性組合,而組合方式也是未知的。同時假設,潛在的變量是非高斯分布且相互獨立的,我們稱之為觀測數據的獨立成分(Independent components)。
ICA與PCA有一定關聯,但是一種更加有用的技術,在經典方法完全失效的時候,可以發現數據源中的潛在因素。它的應用包括數字圖片,文件數據庫,經濟指數和心理測量。
現在可以開始用你對這些算法的理解,去創建機器學習應用,給大家帶來更好的體驗。
 電子發燒友App
電子發燒友App














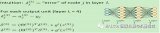











評論