本文主要介紹一個被廣泛使用的機器學習分類算法，K-nearest neighbors（KNN），中文叫K近鄰算法。

KNN

k近鄰算法是一種基本分類和回歸方法。

KNN實際上也可以用于回歸問題，不過在工業界使用得比較廣泛的還是分類問題

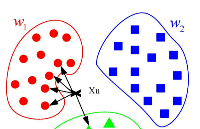
KNN的核心思想也非常簡單，如果一個樣本在特征空間中的k個最相鄰的樣本中的大多數屬于某一個類別，則該樣本也屬于這個類別，比如下圖，當K=3時，節點會被預測屬于紅色橢圓類。有點“近朱者赤，近墨者黑”的感覺。

算法的原理非常簡單，但這其中隱藏了一些值得被探討的點：

? k該如何取值？

? 距離最近中的“距離”是什么，怎么計算會更好？

? 如果對于一個數據要計算它與模型中所有點的距離，那當數據量很大的時候性能會很差，怎么改善？

? 在一些情況下明明數據離某一個點特別近，但有另外兩個同類的點離得很遠但被K包含在內了，這種情況把數據劃為這兩個點的同類是不是不太合理？

? 如果訓練數據不均衡（Imbalance data）怎么辦？

? 特征的緯度量綱跨越很大（比如10和10000）怎么辦？

? 特征中含有類型（顏色：紅黃藍綠）怎么處理？

下面我們一一來解決與KNN相關的一些問題

超參數（Hyperparameter）K的選取

超參數是在開始學習過程之前設置值的參數，而不是通過訓練得到的參數數據。比如：

? 訓練神經網絡的學習速率。

? 學習速率

? 用于支持向量機的C和sigma超參數。

? K最近鄰的K。

KNN中，K越大則類與類的分界會越平緩，K越小則會越陡峭。當K越小時整個模型的錯誤率（Error Rate）會越低（當然過擬合的可能就越大）。

由于KNN一般用于分類，所以K一般是奇數才方便投票

一般情況下，K與模型的validation error（模型應用于驗證數據的錯誤）的關系如下圖所示。

K越小則模型越過擬合，在驗證數據上表現肯定一般，而如果K很大則對某個數據的預測會把很多距離較遠的數據也放入預測，導致預測發生錯誤。所以我們需要針對某一個問題選擇一個最合適的K值，來保證模型的效果最好。本文僅介紹一種“交叉驗證法”，

交叉驗證法（Cross Validation）

在機器學習里，通常來說我們不能將全部用于數據訓練模型，否則我們將沒有數據集對該模型進行驗證，從而評估我們的模型的預測效果。為了解決這一問題，有如下常用的方法：

? The Validation Set Approach

? Cross-Validation

The Validation Set Approach指的是最簡單的，也是很容易就想到的。我們可以把整個數據集分成兩部分，一部分用于訓練，一部分用于驗證，這也就是我們經常提到的訓練集（training set）和驗證集（Validation set）

然而我們都知道，當用于模型訓練的數據量越大時，訓練出來的模型通常效果會越好。所以訓練集和測試集的劃分意味著我們無法充分利用我們手頭已有的數據，所以得到的模型效果也會受到一定的影響。

基于這樣的背景有人就提出了交叉驗證法（Cross-Validation）。

這里簡單介紹下k-fold cross-validation，指的是將所有訓練數據折成k份，如下圖是當折數k=5時的情況。

我們分別使用這5組訓練-驗證數據得到KNN超參數K為某個值的時候，比如K=1的5個準確率，然后將其準確率取平均數得到超參數K為1時的準確率。然后我們繼續去計算K=3 K=5 K=7時的準確率，然后我們就能選擇到一個準確率最高的超參K了。

KNN中的距離

K近鄰算法的核心在于找到實例點的鄰居，那么鄰居的判定標準是什么，用什么來度量？這在機器學習領域其實就是去找兩個特征向量的相似性。機器學習中描述兩個特征向量間相似性的距離公式有很多：

歐氏距離

常見的兩點之間或多點之間的距離表示法

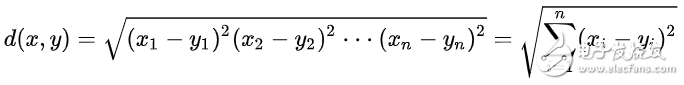
曼哈頓距離

曼哈頓距離指的是在向量在各坐標軸上投影的距離總和，想象你在曼哈頓要從一個十字路口開車到另外一個十字路口，駕駛距離是兩點間的直線距離嗎？顯然不是，除非你能穿越大樓。而實際駕駛距離就是這個“曼哈頓距離”，此即曼哈頓距離名稱的來源， 同時，曼哈頓距離也稱為城市街區距離（City Block distance）。

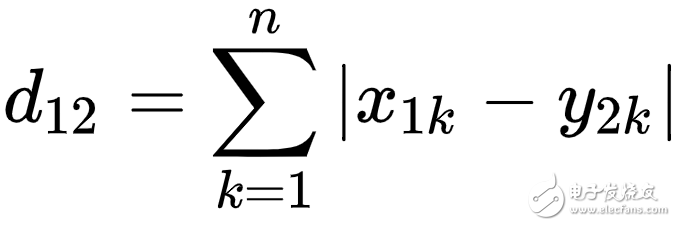
馬氏距離（Mahalanobis Distance）

由印度統計學家馬哈拉諾比斯（P. C. Mahalanobis）提出，表示數據的協方差距離。是一種有效的計算兩個未知樣本集的相似度的方法。與歐氏距離不同的是它考慮到各種特性之間的聯系（例如：一條關于身高的信息會帶來一條關于體重的信息，因為兩者是有關聯的），并且是尺度無關的（scale-invariant），即獨立于測量尺度。如果協方差矩陣為單位矩陣，那么馬氏距離就簡化為歐氏距離。

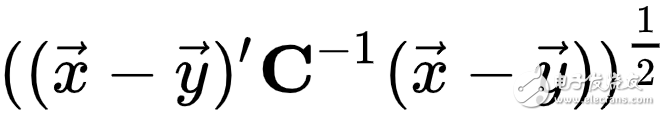
其他

? 切比雪夫距離（Chebyshev distance）

? 閔可夫斯基距離（Minkowski Distance）

? 標準化歐氏距離 （Standardized Euclidean distance ）

? 巴氏距離（Bhattacharyya Distance）

? 漢明距離（Hamming distance）

? 夾角余弦（Cosine）

? 杰卡德相似系數（Jaccard similarity coefficient）

? 皮爾遜系數（Pearson Correlation Coefficient）

大數據性能優化

從原理中很容易知道，最基本的KNN算法的時間復雜度是O（N），因為對于某一個數據，必須計算它必須與模型中的所有點的距離。有沒有辦法優化這部分性能呢？這里主要說下兩個方法。

K-d tree

K-d trees are a wonderful invention that enable O（ klogn） （expected） lookup times for the k nearest points to some point x. This is extremely useful， especially in cases where an O（n） lookup time is intractable already.

其算法的核心思想是分而治之，即將整個空間劃分為幾個小部分。

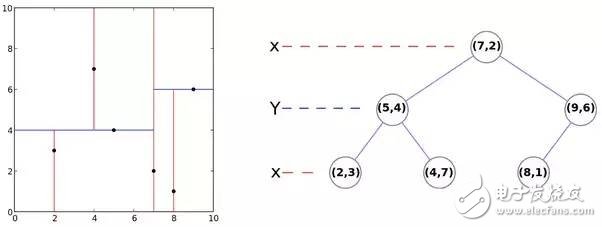
注意K-D樹對于數據緯度d來說是指數級的復雜度，所以只適合用在數據緯度較小的情況。

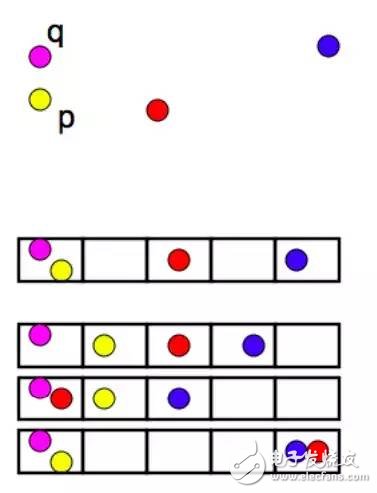
Locality Sensitivity Hasing（LSH）

LSH的基本思想是將數據節點插入Buckets，讓距離近的節點大概率插入同一個bucket中，數據間距離遠的兩個點則大概率在不同的bucket，這使得確定某點最臨近的節點變得更為容易。

所以LSH不能保證一定準確

樣本的重要性

在一些情況下明明數據離某一個點特別近，但有另外兩個同類的點離得很遠但被K包含在內了，這種情況把數據劃為這兩個點的同類是不是不太合理。

例如下圖，當K=3時，紅點會被投票選舉成Offer類，但實際上這個點可能更加適合分類為No Offer。

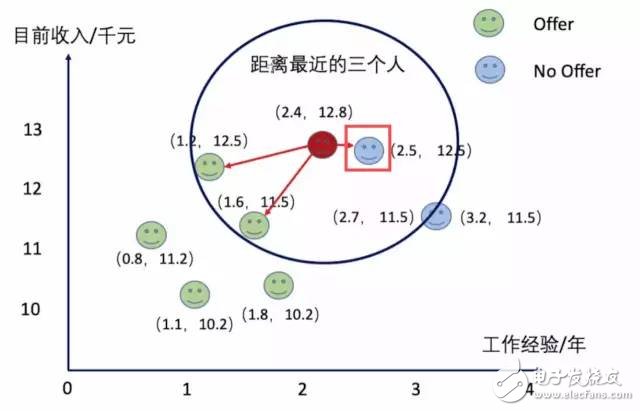
為了解決這一問題有一種方法Distance-weighted nearest neighbor，其核心思想是讓距離近的點可以得到更大的權重。

責任編輯:zl