在平時的科研中,我們經(jīng)常使用統(tǒng)計概率的相關(guān)知識來幫助我們進行城市研究。因此,掌握一定的統(tǒng)計概率相關(guān)知識非常有必要。 本文將討論我們經(jīng)常遇到的概率分布,希望能從概念層面幫助大家建立總體認(rèn)知。
1. 隨機變量
離散隨機變量
隨機實驗的所有可能結(jié)果都是隨機變量。一個隨機變量集合用??表示。 如果實驗可能的結(jié)果是可數(shù)的,那么它被稱為離散隨機變量。例如,如果你拋硬幣 10 次,你能得到的正面數(shù)可以用一個數(shù)字表示。或者籃子里有多少蘋果仍然是可數(shù)的。 連續(xù)隨機變量 這些是不能以離散方式表示的值。例如,一個人可能有 1.7 米高,1米 80 厘米,1.6666666...米高等等。
2. 密度函數(shù)
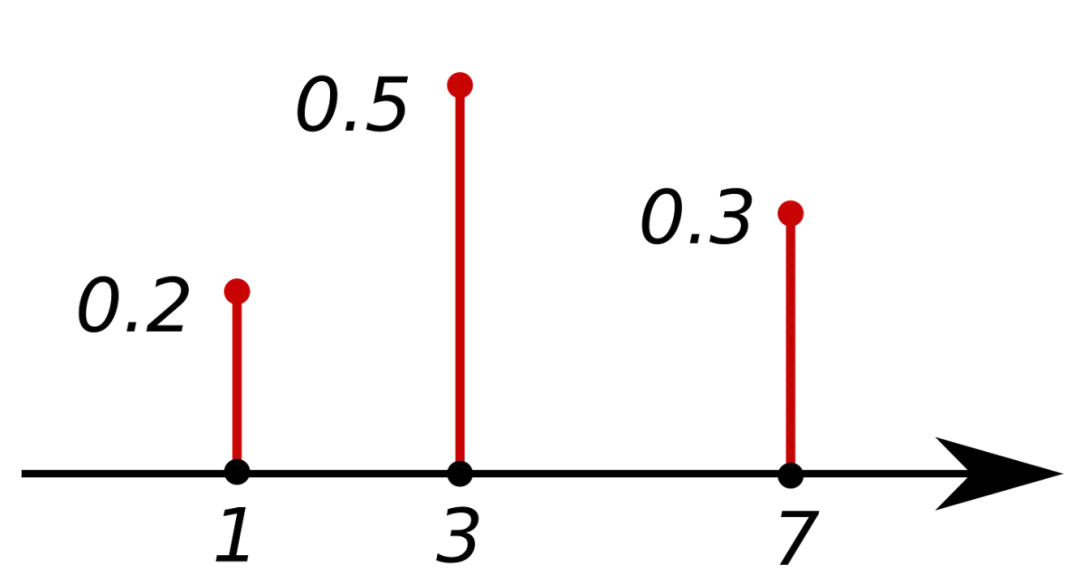
我們使用密度函數(shù)來描述隨機變量??的概率分布。 PMF:概率質(zhì)量函數(shù) 返回離散隨機變量??等于??的值的概率。所有值的總和等于 1。PMF 只能用于離散變量。
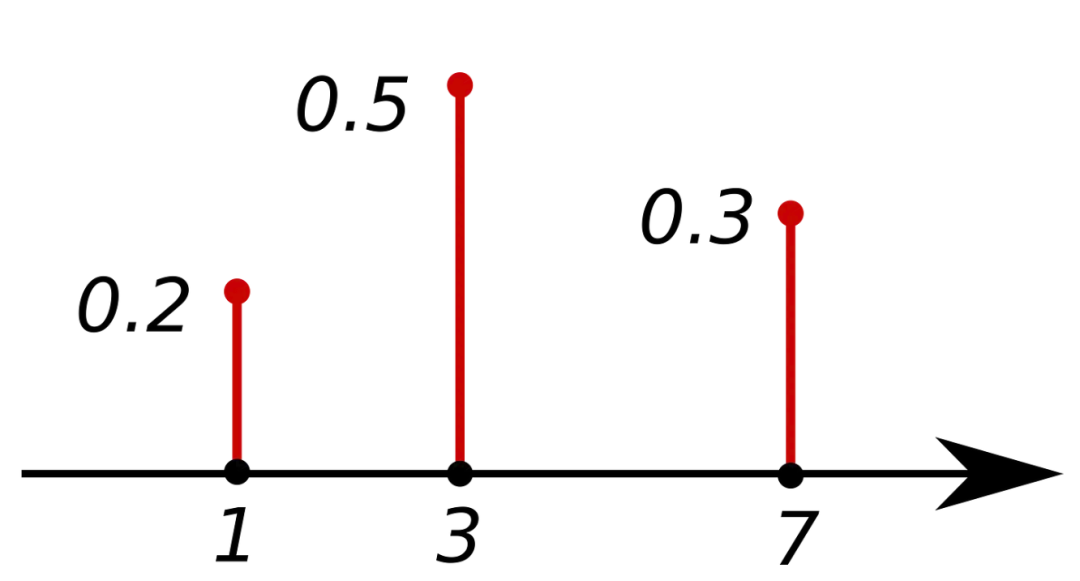
PMF。來源:https://en.wikipedia.org/wiki/Probability_mass_function PDF:概率密度函數(shù) 它類似于連續(xù)變量的 PMF 版本。返回連續(xù)隨機變量 X 在某個范圍內(nèi)的概率。
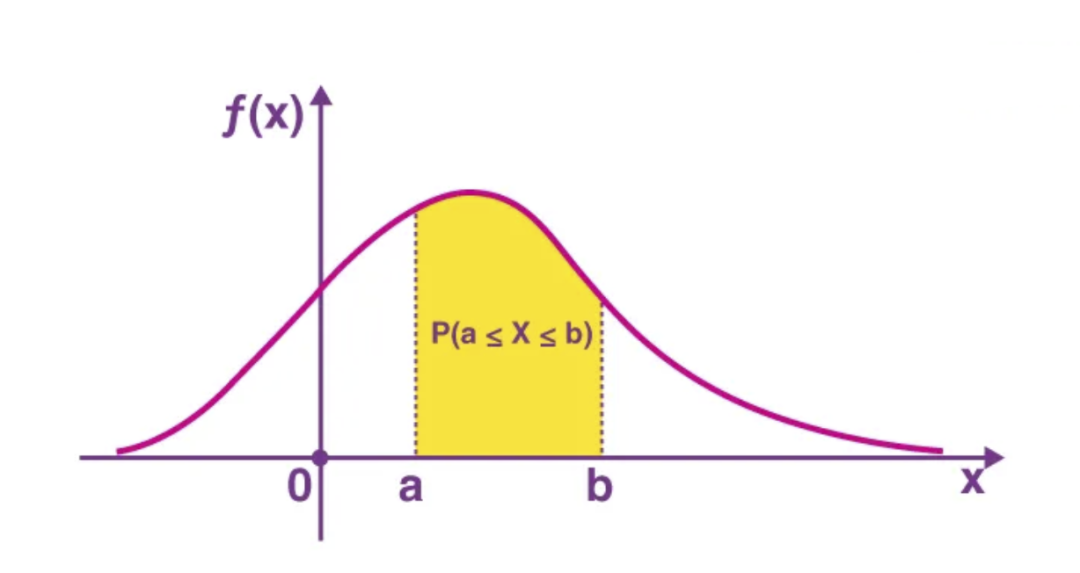
PDF。來源:https://byjus.com/maths/probability-density-function/ CDF:累積分布函數(shù) 返回隨機變量 X 取小于或等于 x 的值的概率。
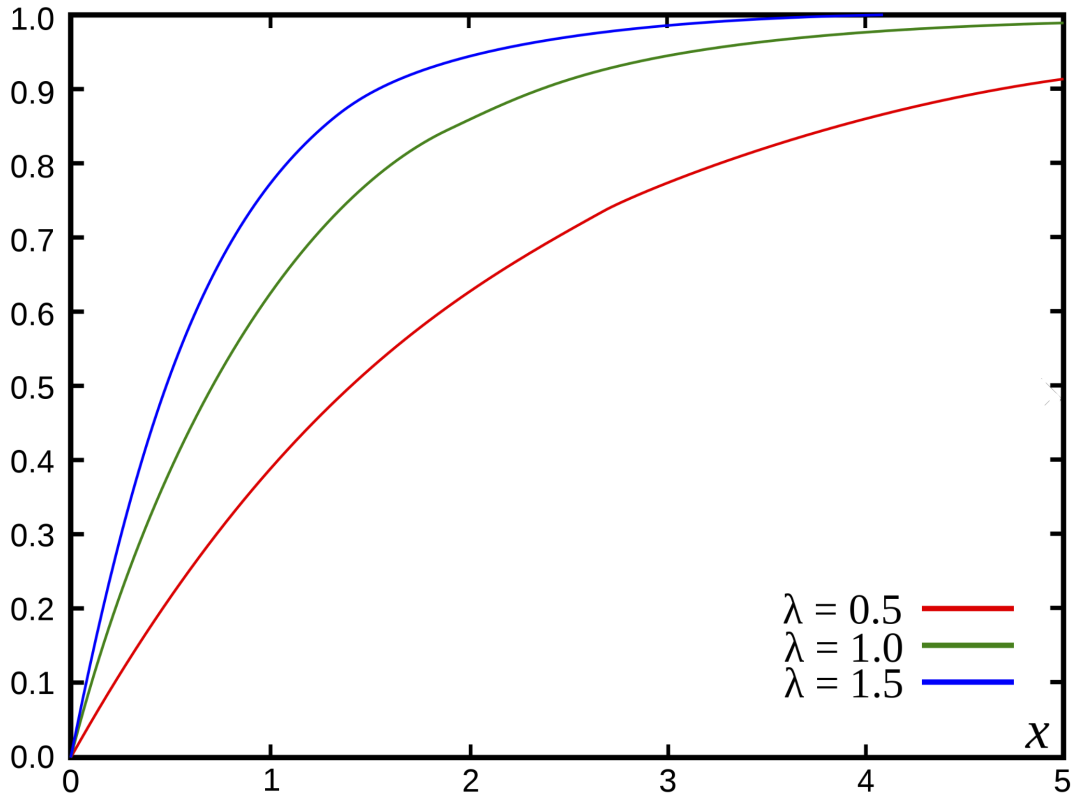
CDF(指數(shù)分布的累積分布函數(shù))。來源:https://en.wikipedia.org/wiki/Cumulative_distribution_function
3. 離散分布
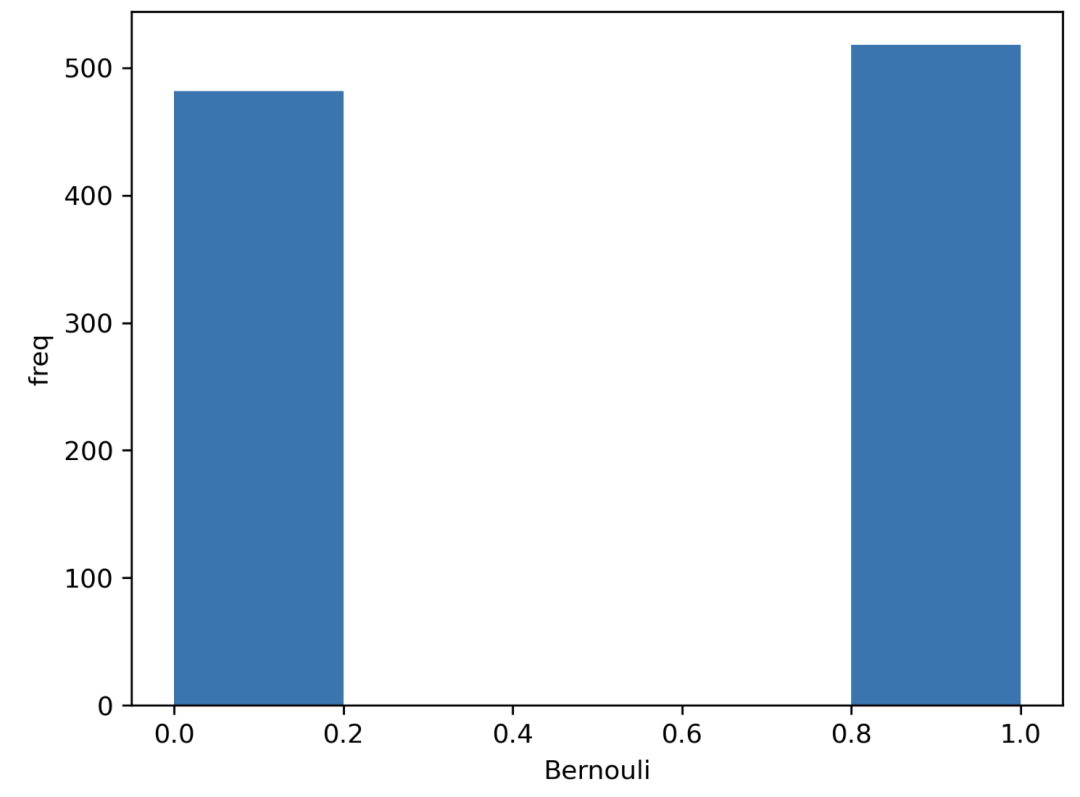
伯努利分布 我們只有一個試驗(只有一個觀察結(jié)果)和兩個可能的結(jié)果。例如,拋硬幣。 我們有一個真的(1)的結(jié)果和一個假的(0)的結(jié)果。假設(shè)我們接受正面為真(我們可以選擇正面為真或成功)。那么,如果正面朝上的概率是 ??,相反情況的概率就是 ??。
import?seaborn?as?sns from?scipy.stats?import?bernoulli #?單一觀察值? #?生成數(shù)據(jù)?(1000?points,?possible?outs:?1?or?0,?probability:?50%?for?each) data?=?bernoulli.rvs(size=1000,p=0.5) #?繪制圖形 ax?=?sns.distplot(data_bern,kde=False,hist_kws={"linewidth":?10,'alpha':1}) ax.set(xlabel='Bernouli',?ylabel='freq')
二項式分布
伯努利分布是針對單個觀測結(jié)果的。多個伯努利觀測結(jié)果會產(chǎn)生二項式分布。例如,連續(xù)拋擲硬幣。 試驗是相互獨立的。一個嘗試的結(jié)果不會影響下一個。 二項式分布可以表示為 ??。??是試驗次數(shù),???是成功的概率。 讓我們進行一個實驗,我們連續(xù)拋擲一枚公平的硬幣 20 次。
import?matplotlib.pyplot?as?plt from?scipy.stats?import?binom n?=?20?? #?實驗次數(shù) p?=?0.5? #?成功的概率 r?=?list(range(n?+?1))? #?the?number?of?success #?pmf值 pmf_list?=?[binom.pmf(r_i,?n,?p)?for?r_i?in?r?] #?繪圖 plt.bar(r,?pmf_list)plt.show()
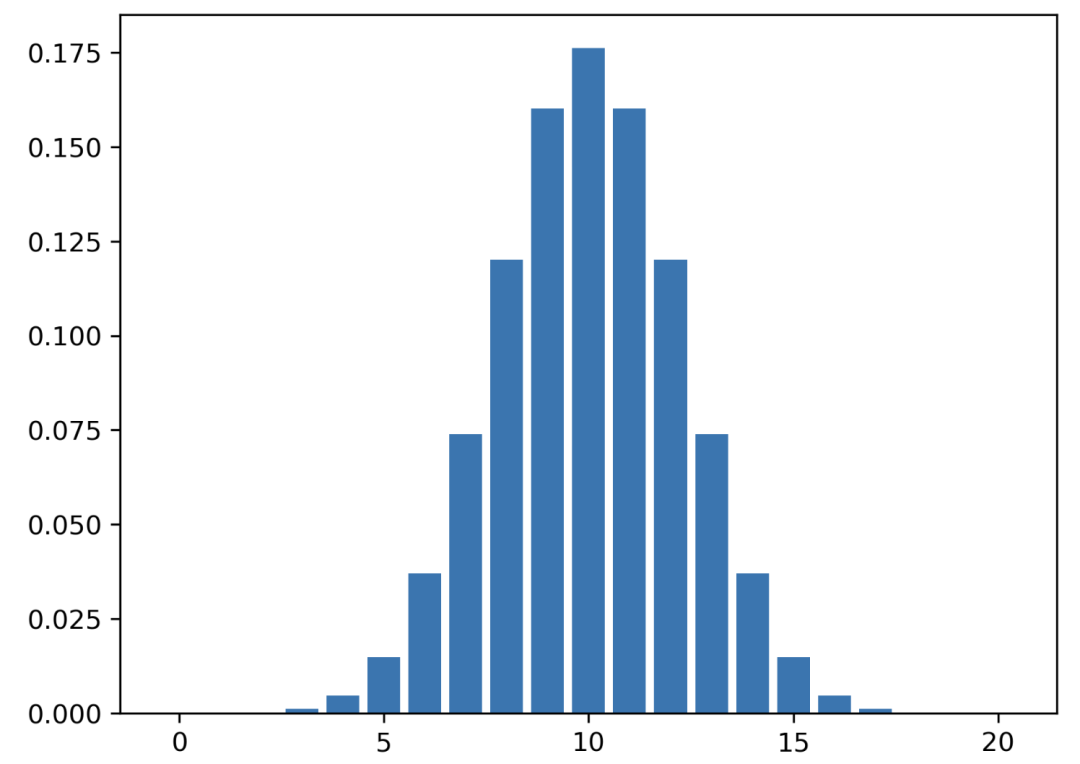
它看起來像正態(tài)分布,但請記住這些值是離散的。
現(xiàn)在這次,你有一枚欺詐硬幣。你知道這個硬幣正面向上的概率是 0.7。因此,p = 0.7。
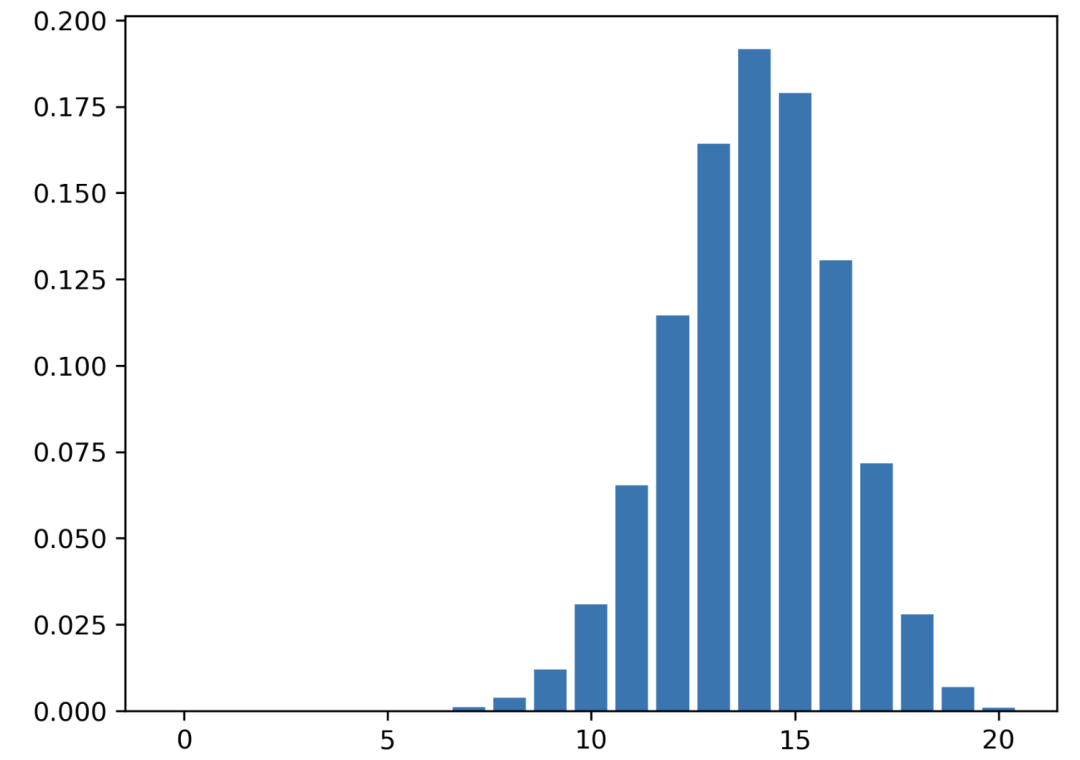
帶有偏差硬幣的二項式分布 該分布顯示出成功結(jié)果數(shù)量增加的概率增加。 ??: 成功的概率??: 實驗次數(shù)??: 失敗的概率?
均勻分布
所有結(jié)果成功的概率相同。擲骰子,1 到 6。
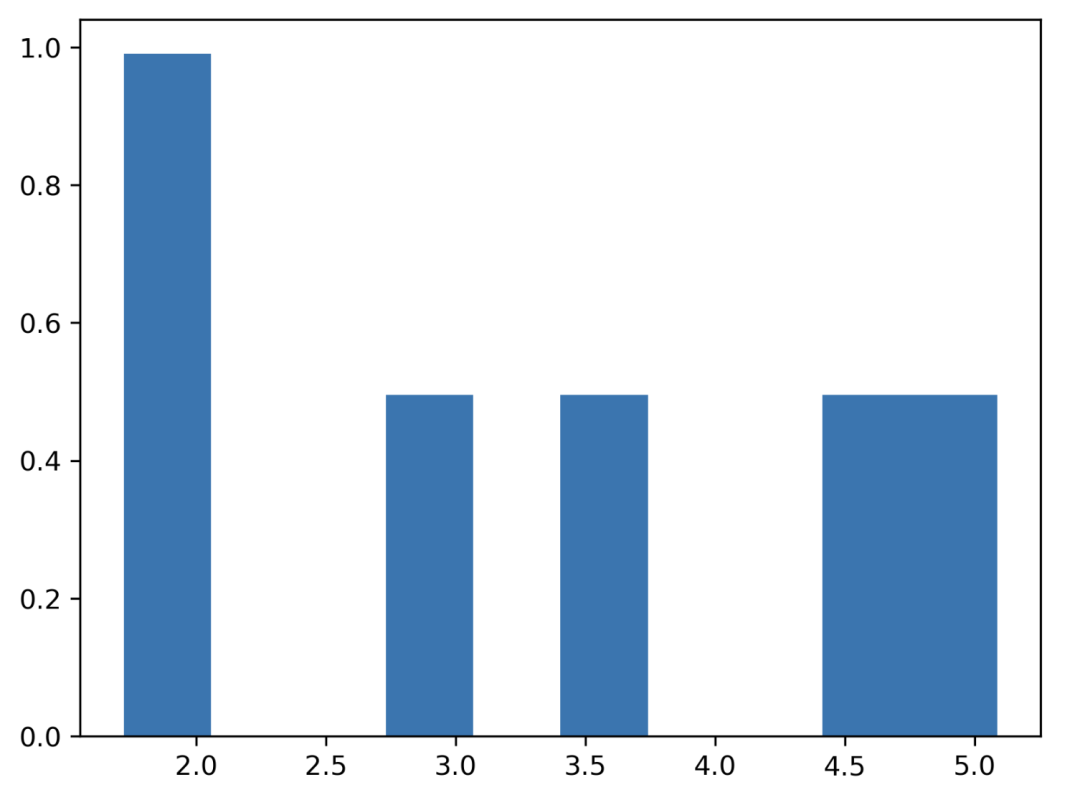
擲 6 次。
data?=?np.random.uniform(1,?6,?6000)
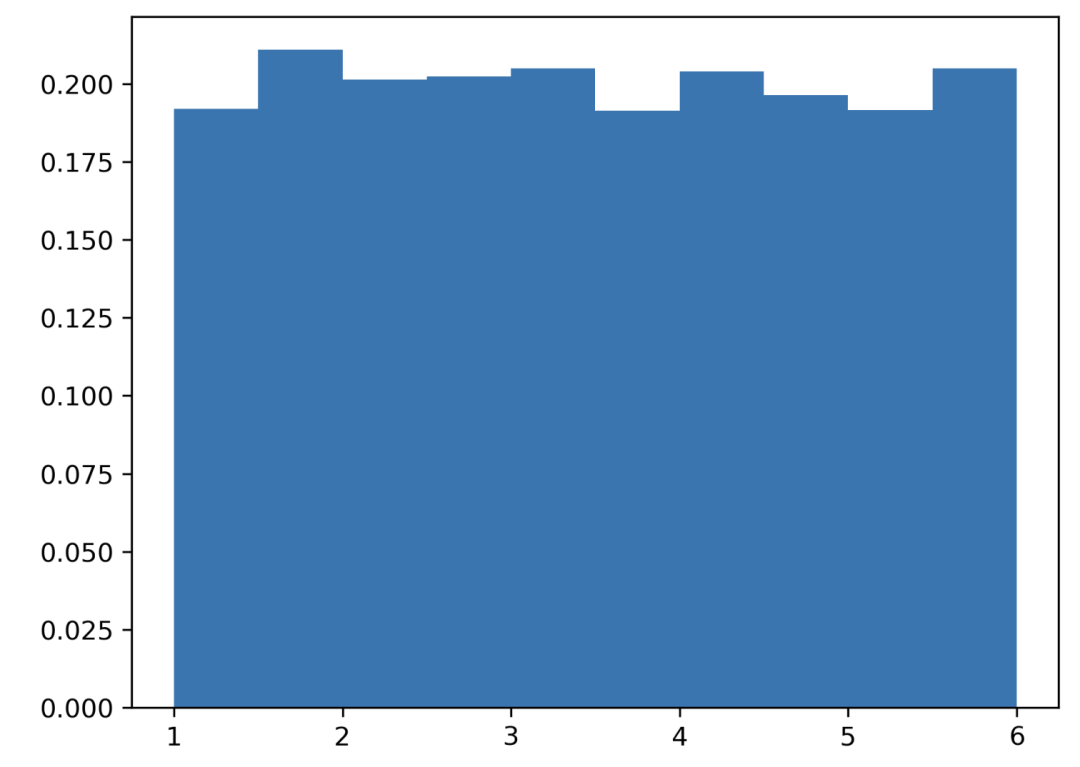
擲 6000 次。
Poisson 分布
它是與事件在給定時間間隔內(nèi)發(fā)生頻率相關(guān)的分布。 ??,??是在指定時間間隔內(nèi)預(yù)期發(fā)生的事件次數(shù)。它是在該時間間隔內(nèi)發(fā)生的事件的已知平均值。??是事件在指定時間間隔內(nèi)發(fā)生的次數(shù)。如果事件遵循泊松分布,則: ?? 在泊松分布中,事件彼此獨立。事件可以發(fā)生任意次數(shù)。兩個事件不能同時發(fā)生。 如每 60 分鐘接到 4 個電話。這意味著 60 分鐘內(nèi)通話的平均次數(shù)為 4。讓我們繪制在 60 分鐘內(nèi)接到 0 到 10 個電話的概率。
import?matplotlib.pyplot?as?plt from?scipy.stats? import?poisson r?=?range(0,11)? #?呼叫次數(shù) lambda_val?=?4? #?均值 #?概率值 data?=?poisson.pmf(r,?lambda_val) #?繪圖 fig,?ax?=?plt.subplots(1,?1,?figsize=(8,?6)) ax.plot(r,?data,?'bo',?ms=8,?label='poisson') plt.ylabel("Probability",?fontsize="12") plt.xlabel("#?Calls",?fontsize="12") plt.title("Poisson?Distribution",?fontsize="16") ax.vlines(r,?0,?data,?colors='r',?lw=5,?alpha=0.5)
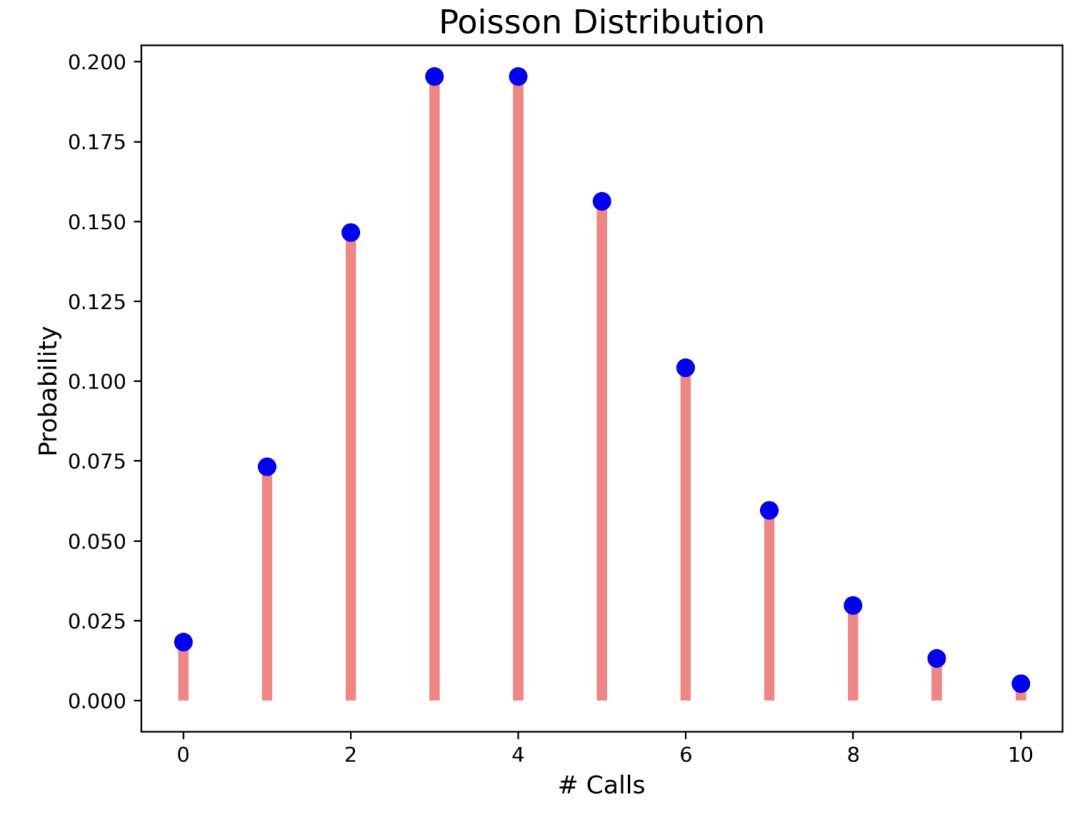
4. 連續(xù)分布
正態(tài)分布
最著名和最常見的分布(也稱為高斯分布),是一種鐘形曲線。它可以通過均值和標(biāo)準(zhǔn)差定義。正態(tài)分布的期望值是均值。 曲線對稱。均值、中位數(shù)和眾數(shù)相等。曲線下總面積為 1。 大約 68%的值落在一個標(biāo)準(zhǔn)差范圍內(nèi)。~95% 落在兩個標(biāo)準(zhǔn)差范圍內(nèi),~98.7% 落在三個標(biāo)準(zhǔn)差范圍內(nèi)。
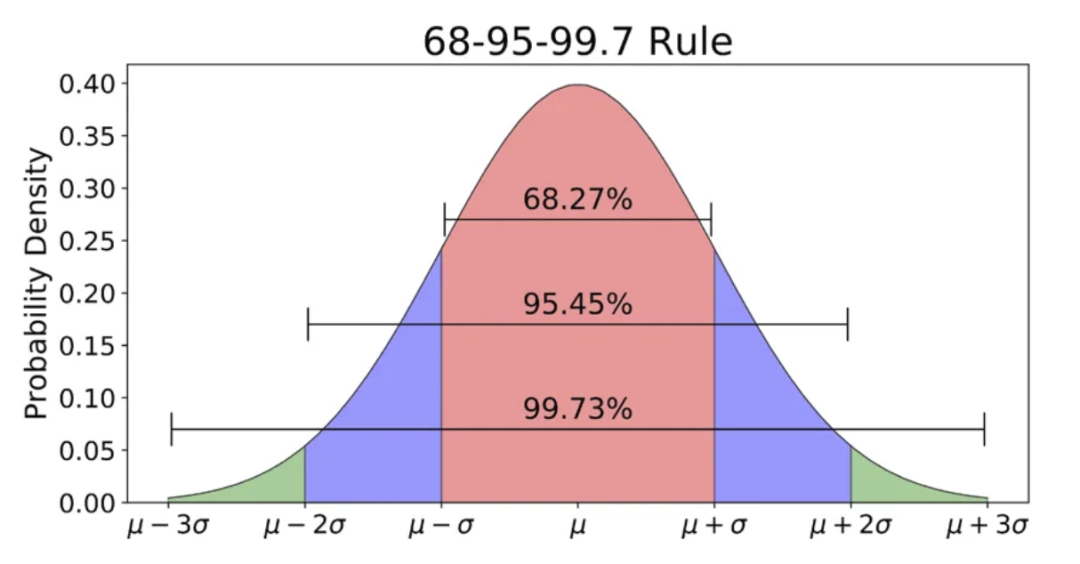
?
import?scipy mean?=?0 standard_deviation?=?5 x_values?=?np.?arange(-30,?30,?0.1) y_values?=?scipy.stats.norm(mean,?standard_deviation) plt.plot(x_values,?y_values.?pdf(x_values))
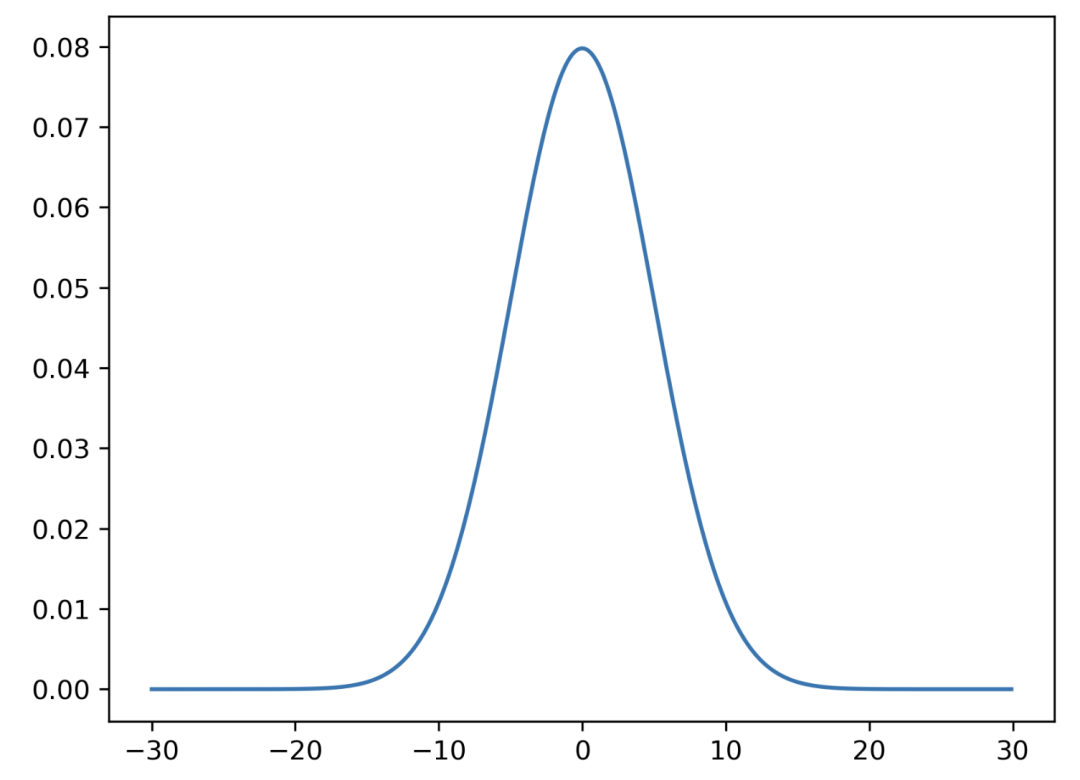
正態(tài)分布的概率密度函數(shù)為: ?? ??是均值,??是常數(shù),??是標(biāo)準(zhǔn)差。
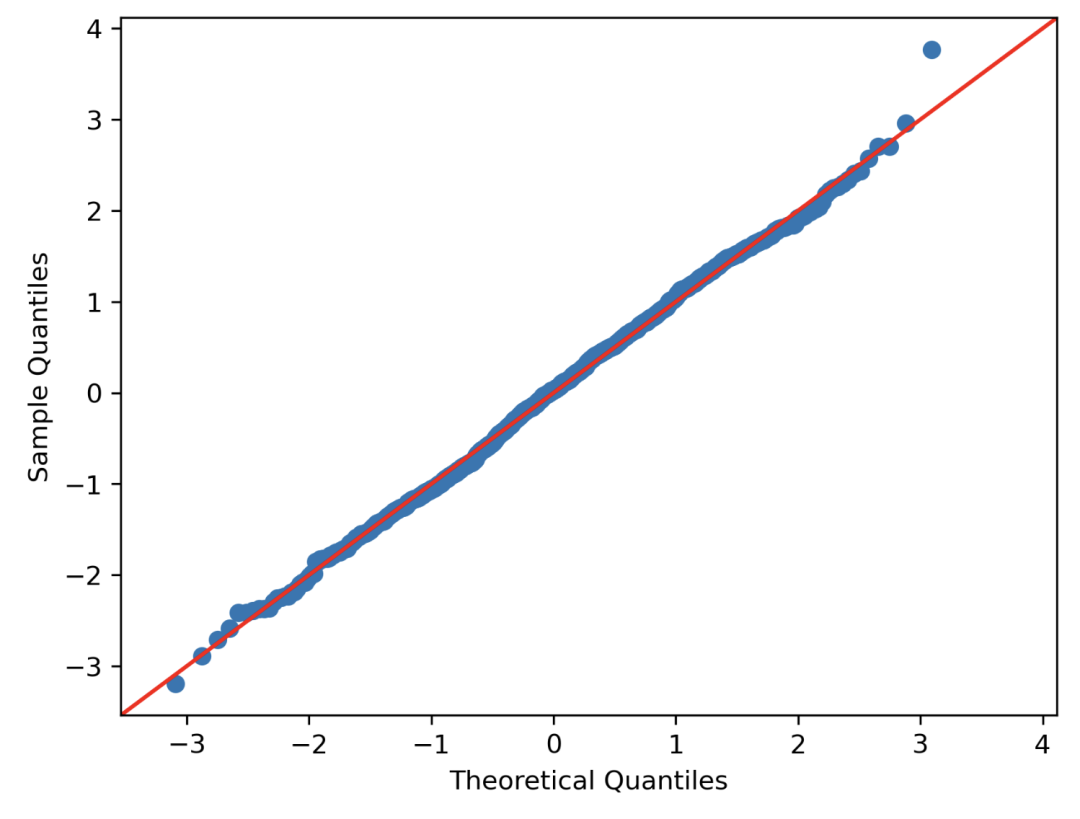
QQ 圖
我們可以使用 QQ 圖來直觀地檢查樣本與正態(tài)分布的接近程度。 計算每個數(shù)據(jù)點的 z 分?jǐn)?shù)并對其進行排序,然后在 y 軸上表示它們。X 軸表示值的排名的分位數(shù)。 這個圖上的點越接近對角線,分布就越接近正態(tài)分布。
import?numpy?as?np import?statsmodels.api?as?sm points?=?np.random.normal(0,?1,?1000) fig?=?sm.qqplot(points,?line?='45') plt.show()
長尾分布
尾巴是分布的長而窄的部分,離群值就位于其中。當(dāng)一側(cè)尾巴不同于另一側(cè)時,就稱為偏斜。下圖是長尾分布的 QQ 圖。
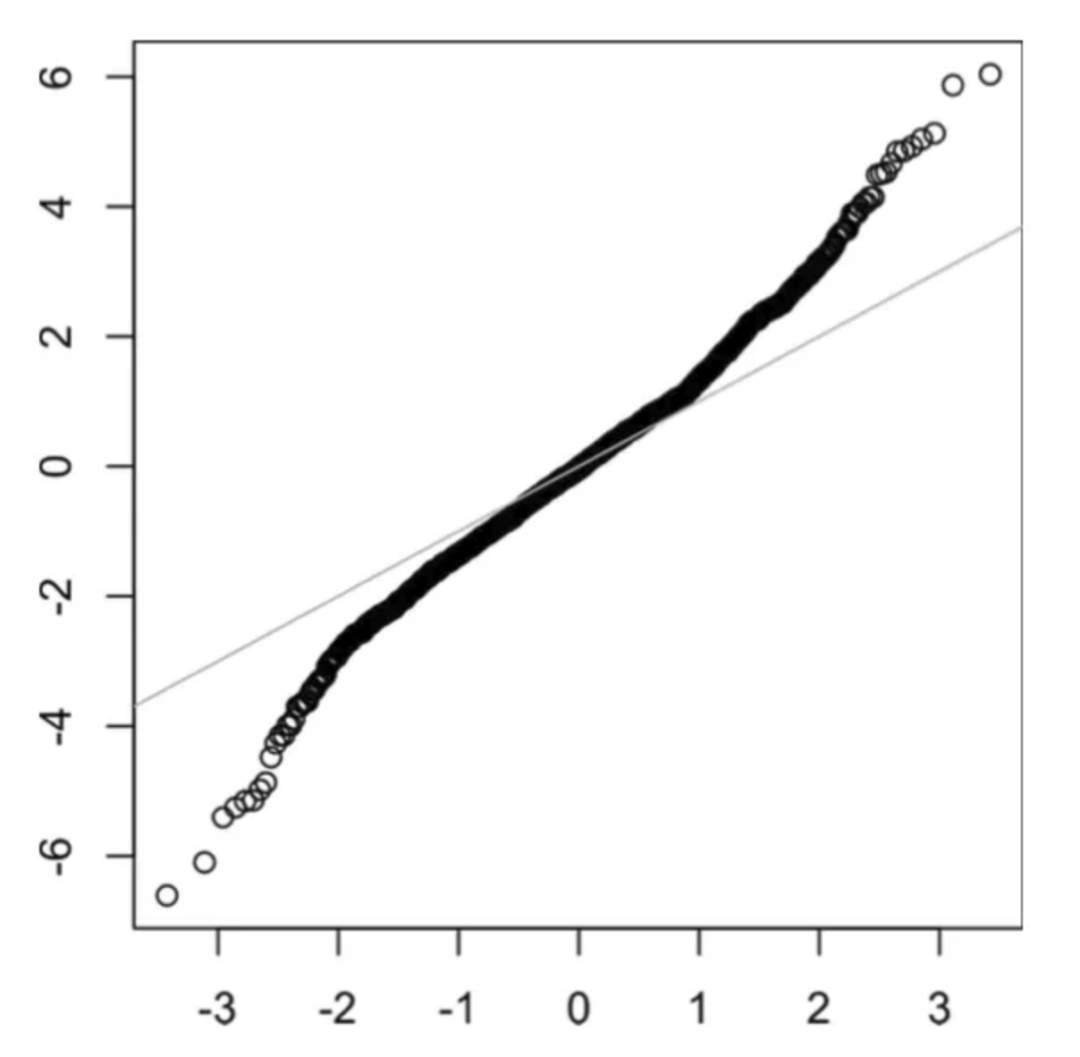
?
import?matplotlib.pyplot?as?plt from?scipy.stats?import?skewnorm def?generate_skew_data(n:?int,?max_val:?int,?skewness:?int):???? ??#?Skewnorm?function???? ??random?=?skewnorm.rvs(a?=?skewness,loc=max_val,?size=n)???? ??plt.hist(random,30,density=True,?color?=?'red',?alpha=0.1)???? ??plt.show() generate_skew_data(1000,?100,?-5)?#?negative?(-5)->?左偏分布
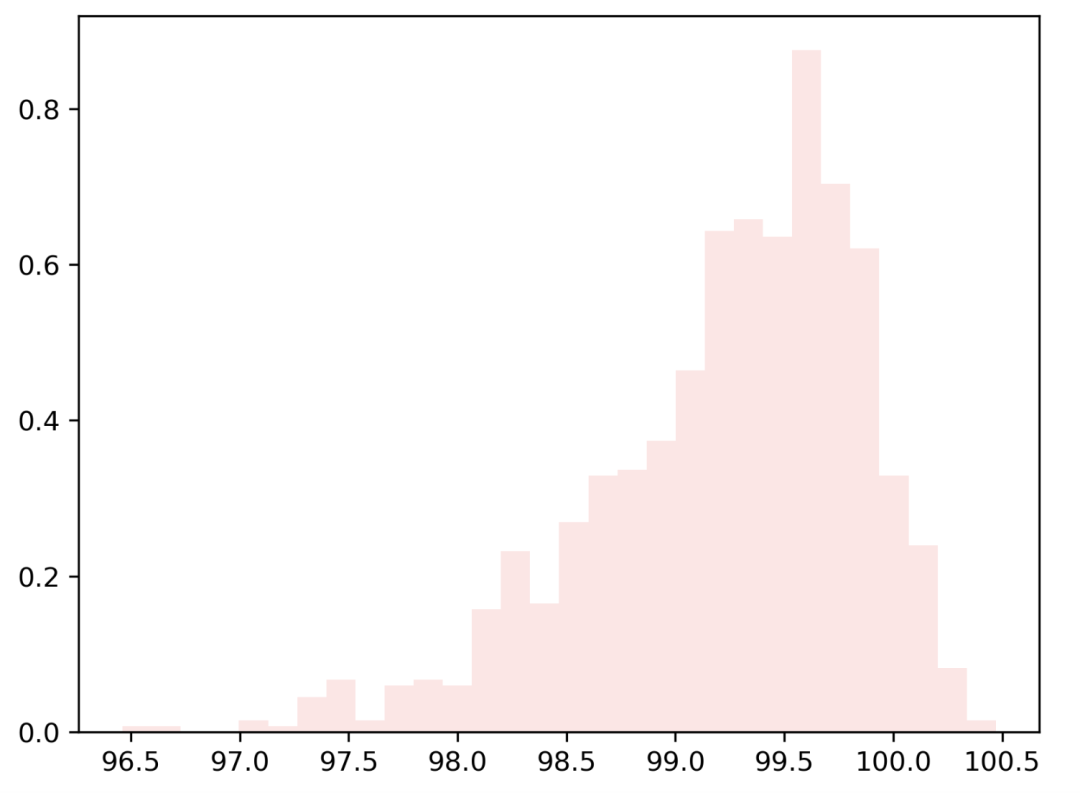
?
?
?
generate_skew_data(1000,?100,?5)?#?positive?(5)->?右偏分布
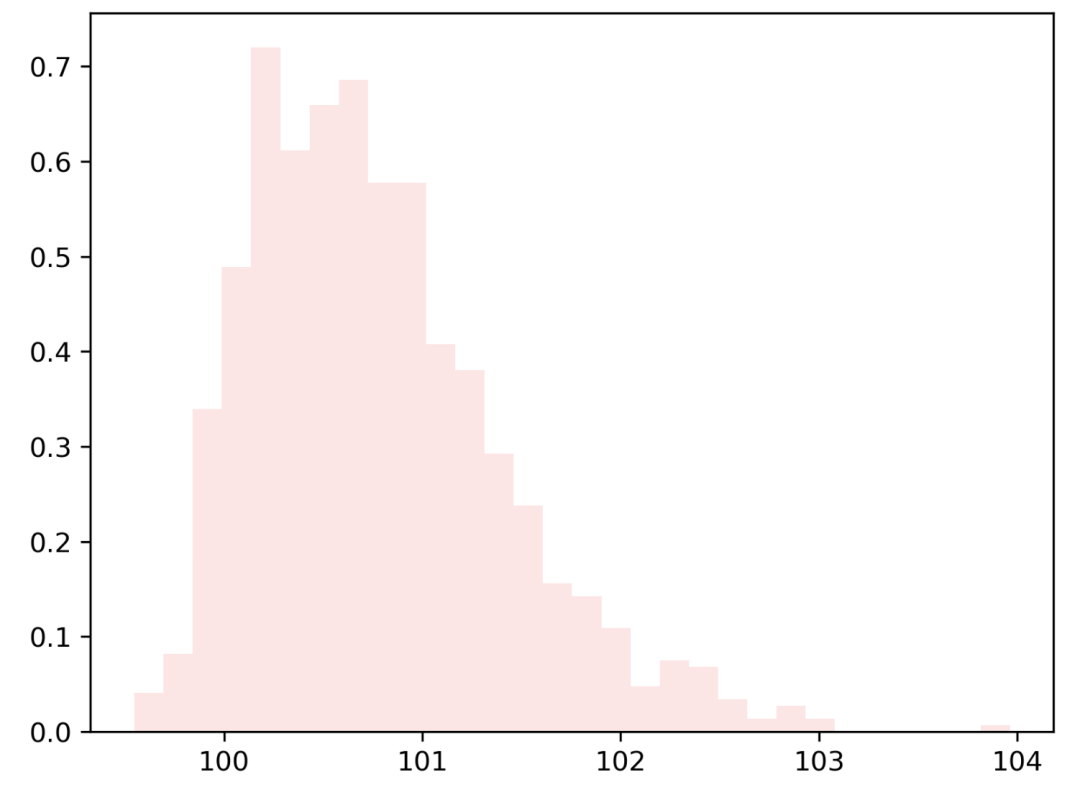
學(xué)生 t 檢驗分布 正態(tài)但有尾(更厚、更長)。
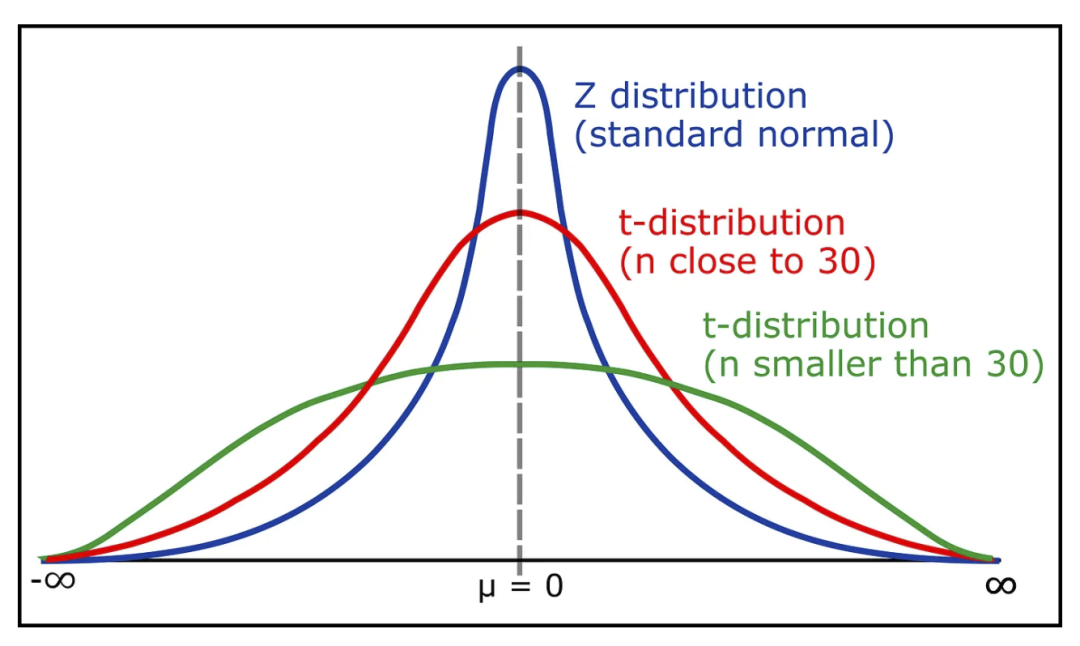
t 分布和 z 分布。來源:https://www.geeksforgeeks.org/students-t-distribution-in-statistics/ t 分布是具有較厚尾部的正態(tài)分布。如果可用數(shù)據(jù)較少(約 30 個),則使用 t 分布代替正態(tài)分布。 在 t 分布中,自由度變量也被考慮在內(nèi)。根據(jù)自由度和置信水平在 t 分布表中找到關(guān)鍵的 t 值。這些值用于假設(shè)檢驗。 t 分布表情移步:https://www.sjsu.edu/faculty/gerstman/StatPrimer/t-table.pdf。
對數(shù)正態(tài)分布
隨機變量 X 的對數(shù)服從正態(tài)分布的分布。
import?numpy?as?np import?matplotlib.pyplot?as?plt from?scipy?import?stats X?=?np.linspace(0,?6,?1500) std?=?1 mean?=?0 lognorm_distribution?=?stats.lognorm([std],?loc=mean) lognorm_distribution_pdf?=?lognorm_distribution.pdf(X) fig,?ax?=?plt.subplots(figsize=(8,?5)) plt.plot(X,?lognorm_distribution_pdf,?label="μ=0,?σ=1") ax.set_xticks(np.arange(min(X),?max(X))) plt.title("Lognormal?Distribution") plt.legend()plt.show()
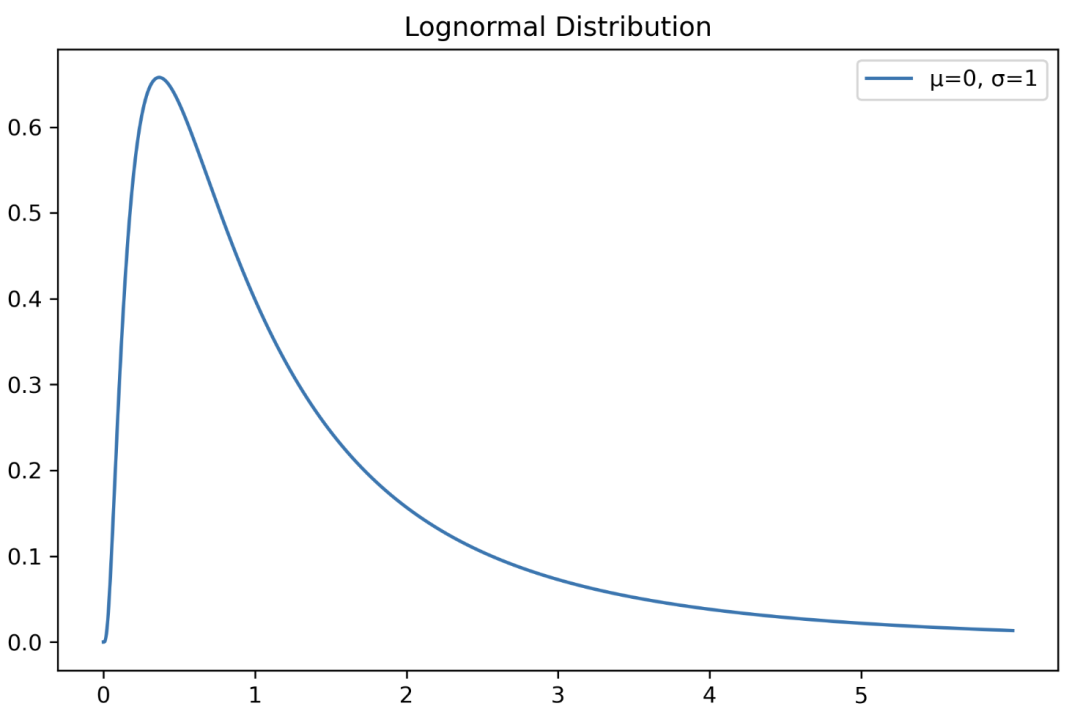
指數(shù)分布
我們在 Poisson 分布中研究了在一定時間間隔內(nèi)發(fā)生的事件。在指數(shù)分布中,我們關(guān)注的是兩個事件之間經(jīng)過的時間。如果我們把上面的例子倒過來,那么兩個電話之間需要多長時間? 因此,如果 X 是一個隨機變量,遵循指數(shù)分布,則累積分布函數(shù)為: ?? ?? ??是均值,??是常數(shù)。
from?scipy.stats?import?expon import?matplotlib.pyplot?as?plt x?=?expon.rvs(scale=2,?size=10000)?#?2?calls #?繪圖 plt.hist(x,?density=True,?edgecolor='black')
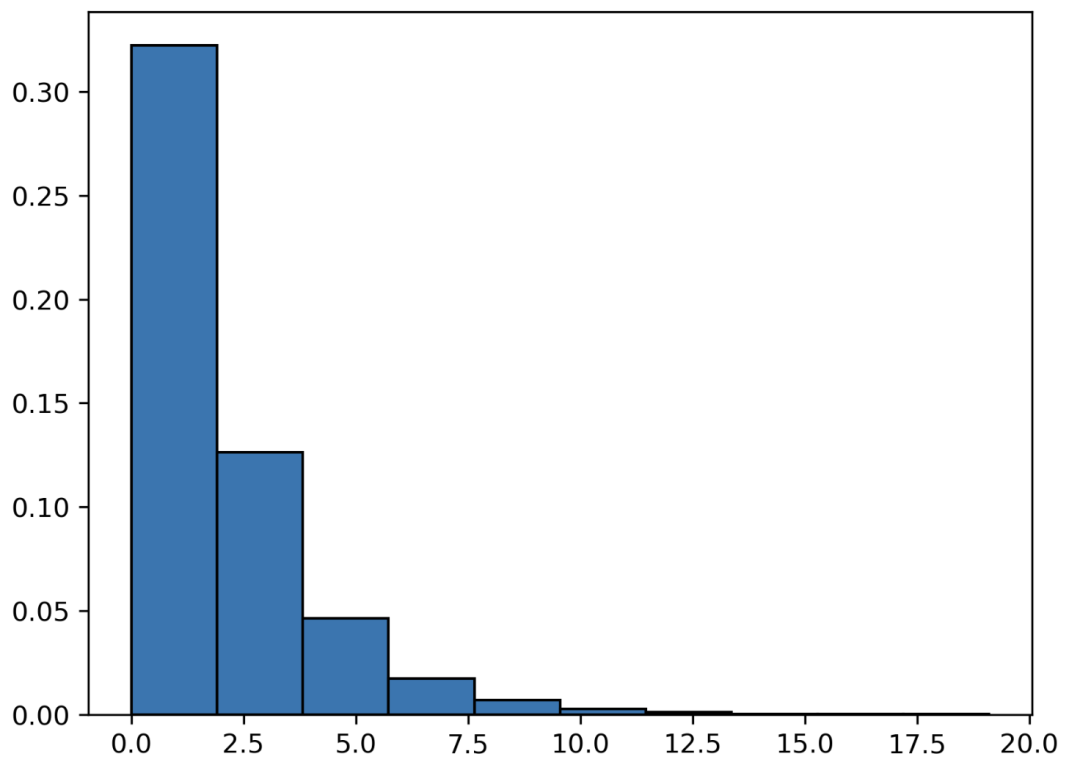
x 軸表示時間間隔的百分比。
韋伯分布
它是指時間間隔是可變的而不是固定的情況下使用的指數(shù)分布的擴展。在 Weibull 分布中,時間間隔被允許動態(tài)變化。 ??是形狀參數(shù),如果是正值,則事件發(fā)生的概率隨時間而增加,反之亦然。??是尺度參數(shù)。
import?matplotlib.pyplot?as?plt x?=?np.arange(1,100.)/50. def?weib(x,n,a):???? ??return?(a?/?n)?*?(x?/?n)**(a?-?1)?*?np.exp(-(x?/?n)**a) count,?bins,?ignored?=?plt.hist(np.random.weibull(5.,1000)) x?=?np.arange(1,100.)/50. scale?=?count.max()/weib(x,?1.,?5.).max() plt.plot(x,?weib(x,?1.,?5.)*scale) plt.show()
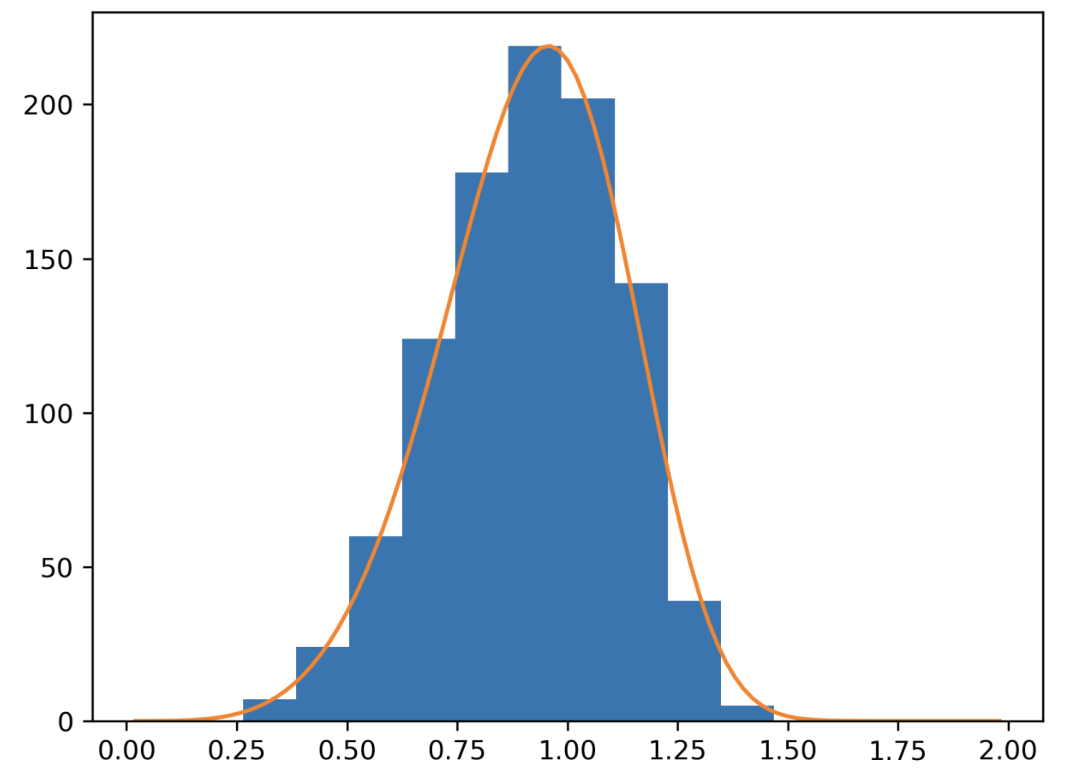
Gamma 分布
指與第 n 個事件發(fā)生所需的時間有關(guān)的分布,而指數(shù)分布則與首次事件發(fā)生的時間有關(guān)。
import?numpy?as?np import?scipy.stats?as?stats import?matplotlib.pyplot?as?plt #Gamma?distributions x?=?np.linspace(0,?60,?1000) y1?=?stats.gamma.pdf(x,?a=5,?scale=3) y2?=?stats.gamma.pdf(x,?a=2,?scale=5) y3?=?stats.gamma.pdf(x,?a=4,?scale=2) #?plots plt.plot(x,?y1,?label='shape=5,?scale=3') plt.plot(x,?y2,?label='shape=2,?scale=5') plt.plot(x,?y3,?label='shape=4,?scale=2') #add?legend plt.legend() #display? plotplt.show()
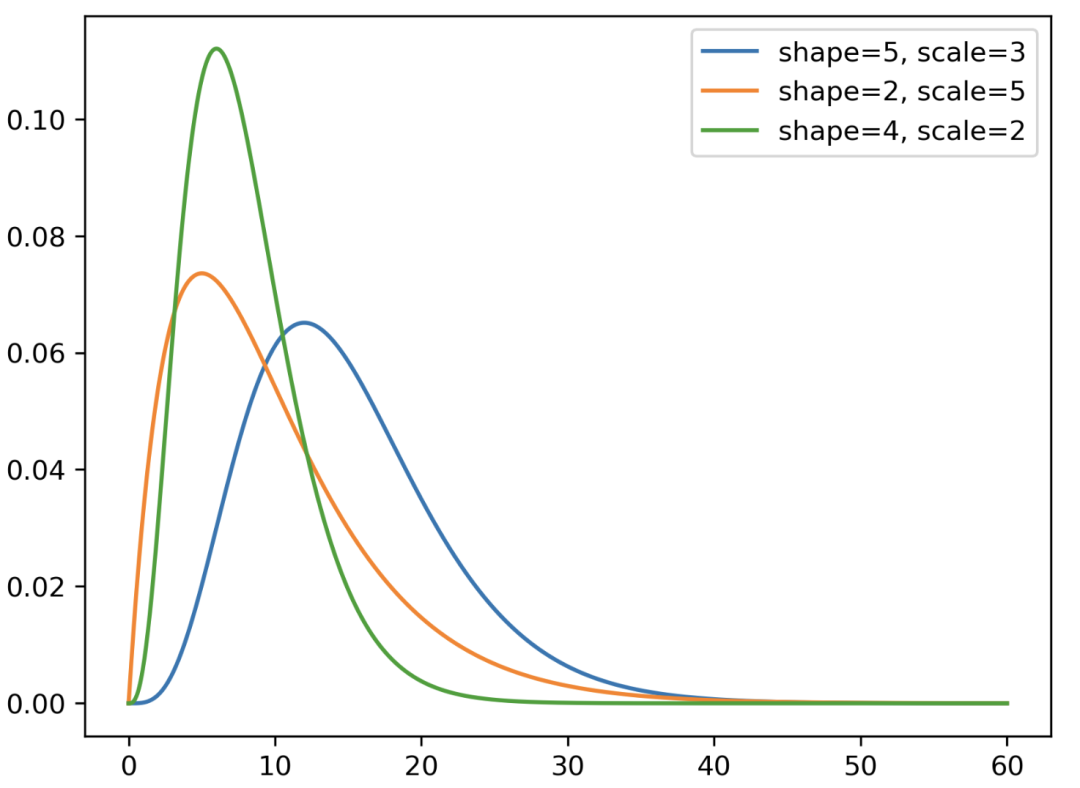
Gamma 分布。X 軸表示隨機變量 X 可能取到的潛在值,Y 軸表示分布的概率密度函數(shù)(PDF)值。
Gamma 分布
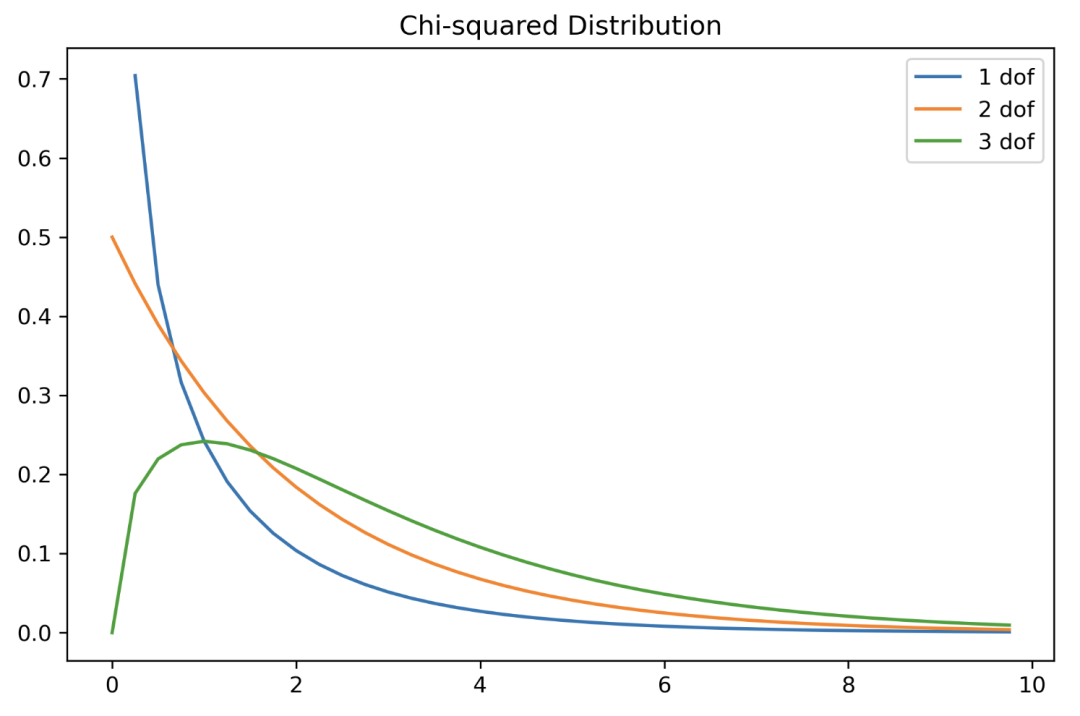
它用于統(tǒng)計檢驗。這通常在實際分布中不會出現(xiàn)。
#?x軸范圍0-10,步長0.25 X?=?np.arange(0,?10,?0.25) plt.subplots(figsize=(8,?5)) plt.plot(X,?stats.chi2.pdf(X,?df=1),?label="1?dof") plt.plot(X,?stats.chi2.pdf(X,?df=2),?label="2?dof") plt.plot(X,?stats.chi2.pdf(X,?df=3),?label="3?dof") plt.title("Chi-squared?Distribution") plt.legend() plt.show()
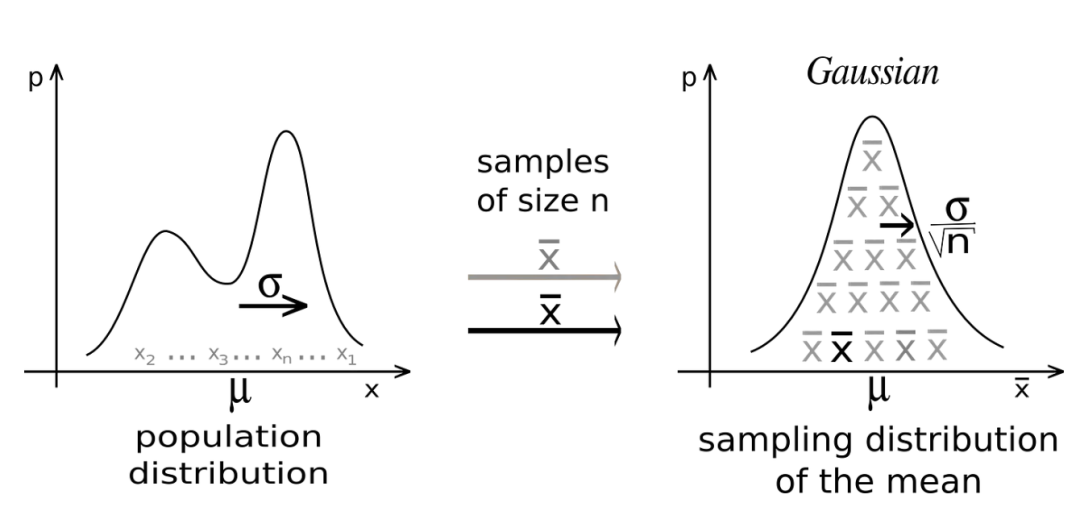
中心極限定理
當(dāng)我們從人群中收集足夠大的樣本時,樣本的平均值將具有正態(tài)分布,即使人群不是正態(tài)分布。
我們可以從任何分布(離散或連續(xù))開始,從人群中收集樣本并記錄這些樣本的平均值。隨著我們繼續(xù)采樣,我們會注意到平均值的分布正在慢慢形成正態(tài)分布。
審核編輯:黃飛
?
 電子發(fā)燒友App
電子發(fā)燒友App










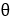
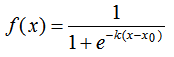











評論