在實際應用中，很多模型都要被部屬在移動端。移動端的存儲空間以及算力都有限，無法運行太大的模型。因此模型壓縮是一項十分關鍵的技術。本文介紹了卷積網絡壓縮的常見方法：低秩近似、剪枝與稀疏約束、參數量化、二值化網絡、知識蒸餾和淺層/輕量網絡。

我們知道，在一定程度上，網絡越深，參數越多，模型越復雜，其最終效果越好。神經網絡的壓縮算法是，旨在將一個龐大而復雜的預訓練模型（pre-trained model）轉化為一個精簡的小模型。按照壓縮過程對網絡結構的破壞程度，我們將模型壓縮技術分為“前端壓縮”和“后端壓縮”兩部分。 前端壓縮，是指在不改變原網絡結構的壓縮技術，主要包括知識蒸餾、緊湊的模型結構涉及以及濾波器（filter）層面的剪枝等。 后端壓縮，是指包括低秩近似、未加限制的剪枝、參數量化以及二值網絡等，目標在于盡可能減少模型大小，會對原始網絡結構造成極大程度的改造。 總結：前端壓縮幾乎不改變原有網絡結構（僅僅只是在原模型基礎上減少了網絡的層數或者濾波器個數），后端壓縮對網絡結構有不可逆的大幅度改變，造成原有深度學習庫、甚至硬件設備不兼容改變之后的網絡。其維護成本很高。

1. 低秩近似

簡單理解就是，卷積神經網絡的權重矩陣往往稠密且巨大，從而計算開銷大，有一種辦法是采用低秩近似的技術將該稠密矩陣由若干個小規模矩陣近似重構出來，這種方法歸類為低秩近似算法。

一般地，行階梯型矩陣的秩等于其“臺階數”----非零行的行數。

低秩近似算法能減小計算開銷的原理如下： 給定權重矩陣?, 若能將其表示為若干個低秩矩陣的組合, 即?, 其中??為低秩矩陣, 其秩為?, 并滿足?, 則其每一個低秩矩陣都可分解為小規模矩陣的乘積,??，其中?,??。當??取值很小時, 便能大幅降低總體的存儲和計算開銷。 基于以上想法, Sindhwani 等人提出使用結構化矩陣來進行低秩分解的算法, 具體原理可自行參考論文。另一種比較簡便的方法 是使用矩陣分解來降低權重矩陣的參數, 如 Denton 等人提出使用奇異值分解（Singular Value Decomposition, 簡稱 SVD）分解 來重構全連接層的權重。

總結

低秩近似算法在中小型網絡模型上，取得了很不錯的效果，但其超參數量與網絡層數呈線性變化趨勢，隨著網絡層數的增加與模型復雜度的提升，其搜索空間會急劇增大，目前主要是學術界在研究，工業界應用不多。

2. 剪枝與稀疏約束

給定一個預訓練好的網絡模型，常用的剪枝算法一般都遵從如下操作：

衡量神經元的重要程度。

移除掉一部分不重要的神經元，這步比前 1 步更加簡便，靈活性更高。

對網絡進行微調，剪枝操作不可避免地影響網絡的精度，為防止對分類性能造成過大的破壞，需要對剪枝后的模型進行微調。對于大規模行圖像數據集（如ImageNet）而言，微調會占用大量的計算資源，因此對網絡微調到什么程度，是需要斟酌的。

返回第一步，循環進行下一輪剪枝。

基于以上循環剪枝框架，不同學者提出了不同的方法，Han等人提出首先將低于某個閾值的權重連接全部剪除，之后對剪枝后的網絡進行微調以完成參數更新的方法，這種方法的不足之處在于，剪枝后的網絡是非結構化的，即被剪除的網絡連接在分布上，沒有任何連續性，這種稀疏的結構，導致CPU高速緩沖與內存頻繁切換，從而限制了實際的加速效果。 基于此方法，有學者嘗試將剪枝的粒度提升到整個濾波器級別，即丟棄整個濾波器，但是如何衡量濾波器的重要程度是一個問題，其中一種策略是基于濾波器權重本身的統計量，如分別計算每個濾波器的 L1 或 L2 值，將相應數值大小作為衡量重要程度標準。 利用稀疏約束來對網絡進行剪枝也是一個研究方向，其思路是在網絡的優化目標中加入權重的稀疏正則項，使得訓練時網絡的部分權重趨向于 0 ，而這些 0 值就是剪枝的對象。

總結

總體而言，剪枝是一項有效減小模型復雜度的通用壓縮技術，其關鍵之處在于如何衡量個別權重對于整體模型的重要程度。剪枝操作對網絡結構的破壞程度極小，將剪枝與其他后端壓縮技術相結合，能夠達到網絡模型最大程度壓縮，目前工業界有使用剪枝方法進行模型壓縮的案例。

3. 參數量化

相比于剪枝操作，參數量化則是一種常用的后端壓縮技術。所謂“量化”，是指從權重中歸納出若干“代表”，由這些“代表”來表示某一類權重的具體數值。“代表”被存儲在碼本（codebook）之中，而原權重矩陣只需記錄各自“代表”的索引即可，從而極大地降低了存儲開銷。這種思想可類比于經典的詞包模型（bag-of-words model）。常用量化算法如下：

標量量化（scalar quantization）。

標量量化會在一定程度上降低網絡的精度，為避免這個弊端，很多算法考慮結構化的向量方法，其中一種是乘積向量（Product Quantization, PQ），詳情咨詢查閱論文。

以PQ方法為基礎，Wu等人設計了一種通用的網絡量化算法：QCNN(quantized CNN)，主要思想在于Wu等人認為最小化每一層網絡輸出的重構誤差，比最小化量化誤差更有效。

標量量化算法基本思路是, 對于每一個權重矩陣?, 首先將其轉化為向量形式:??。之后對該權重向量 的元素進行??個簇的聚類, 這可借助于經典的 k-均值 (k-means) 聚類算法快速完成: ? 這樣，只需將??個聚類中心?，標量??存儲在碼本中，而原權重矩陣則只負責記錄各自聚類中心在碼本中索引。如果不 考慮碼本的存儲開銷，該算法能將存儲空間減少為原來的?。基于??均值算法的標量量化在很多應用中非常有效。參數量化與碼本微調過程圖如下:

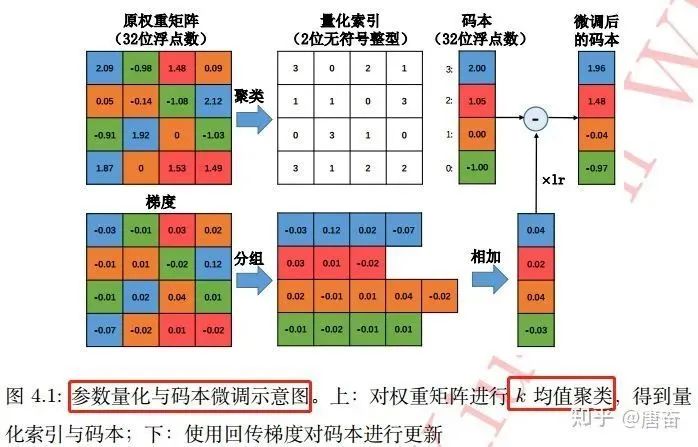
這三類基于聚類的參數量化算法，其本質思想在于將多個權重映射到同一個數值，從而實現權重共享，降低存儲開銷的目的。

總結

參數量化是一種常用的后端壓縮技術，能夠以很小的性能損失實現模型體積的大幅下降，不足之處在于，量化的網絡是“固定”的，很難對其做任何改變，同時這種方法通用性差，需要配套專門的深度學習庫來運行網絡。

4. 二值化網絡

二值化網絡可以視為量化方法的一種極端情況：所有的權重參數取值只能為??，也就是使用 1bit 來存儲 Weight 和 Feature。在普通神經網絡中，一個參數是由單精度浮點數來表示的，參數的二值化能將存儲開銷降低為原來的 1/32。

二值化神經網絡以其高的模型壓縮率和在前傳中計算速度上的優勢，近幾年格外受到重視和發展，成為神經網絡模型研究中的非常熱門的一個研究方向。但是，第一篇真正意義上將神經網絡中的權重值和激活函數值同時做到二值化的是 Courbariaux 等人 2016 年發表的名為《Binarynet: Training deep neural networks with weights and activations constrained to +1 or -1》的一篇論文。這篇論文第一次給出了關于如何對網絡進行二值化和如何訓練二值化神經網絡的方法。

CNN 網絡一個典型的模坱是由卷積(Conv)->批標準化(BNorm)->激活(Activ)->池化??Pool)這樣的順序操作組成的。對于異或神經網絡，設計出的模塊是由批標準化??二值化激活(BinActiv) ->二值化卷積(BinConv)->池化 (Pool)的順序操作完成。這樣做的原因是批標準化以后，保證了輸入均值為 0 ，然后進行二值化激活，保證了數據為??或者?，然后進行二值化卷積，這樣能最大程度上減少特征信息的損失。二值化殘差網絡結構定義實例代碼如下：

def?residual_unit(data,?num_filter,?stride,?dim_match,?num_bits=1): ???
?"""殘差塊?Residual?Block?定義 ????""" ????
bnAct1?=?bnn.BatchNorm(data=data,?num_bits=num_bits) ??
??conv1?=?bnn.Convolution(data=bnAct1,?num_filter=num_filter,?kernel=(3,?3),?stride=stride,?pad=(1,?1)) ??
??convBn1?=?bnn.BatchNorm(data=conv1,?num_bits=num_bits) ????
conv2?=?bnn.Convolution(data=convBn1,?num_filter=num_filter,?kernel=(3,?3),?stride=(1,?1),?pad=(1,?1)) ????if?dim_match: ???
?????shortcut?=?data ????else: ????????
shortcut?=?bnn.Convolution(data=bnAct1,?num_filter=num_filter,?kernel=(3,?3),?stride=stride,?pad=(1,?1)) ????return?conv2?+?shortcut

4.1 二值網絡的梯度下降

現在的神經網絡幾乎都是基于梯度下降算法來訓練的，但是二值網絡的權重只有±1，無法直接計算梯度信息，也無法進行權重更新。為解決這個問題，Courbariaux 等人提出二值連接（binary connect）算法，該算法采取單精度與二值結合的方式來訓練二值神經網絡（），這是第一次給出了關于如何對網絡進行二值化和如何訓練二值化神經網絡的方法。過程如下：

權重 weight 初始化為浮點

前向傳播 Forward Pass：

-利用決定化方式（sign(x)函數）把 Weight 量化為 +1/-1, 以0為閾值 - 利用量化后的 Weight (只有+1/-1)來計算前向傳播，由二值權重與輸入進行卷積運算（實際上只涉及加法），獲得卷積層輸出。

反向傳播 Backward Pass：把梯度更新到浮點的 Weight 上（根據放松后的符號函數，計算相應梯度值，并根據該梯度的值對單精度的權重進行參數更新）；訓練結束：把 Weight 永久性轉化為 +1/-1, 以便 inference 使用。

4.2 兩個問題

網絡二值化需要解決兩個問題：如何對權重進行二值化和如何計算二值權重的梯度。

如何對權重進行二值化? 權重二值化一般有兩種選擇：

直接根據權重的正負進行二值化:??。符號函數??定義如下：

進行隨機的二值化，即對每一個權重, 以一定概率取??。

如何計算二值權重的梯度? 二值權重的梯度為 0 ，無法進行參數更新。為解決這個問題，需要對符號函數進行放松，即用??來代替??。當??在區間??時，存在梯度值 1，否則梯度為 0 。

4.3 二值連接算法改進

之前的二值連接算法只對權重進行了二值化，但是網絡的中間輸出值依然是單精度的，于是 Rastegari 等人對此進行了改進，提出用單精度對角陣與二值矩陣之積來近似表示原矩陣的算法，以提升二值網絡的分類性能，彌補二值網絡在精度上弱勢。該算法 將原卷積運算分解為如下過程： ? 其中??為該層的輸入張量,??為該層的一個濾波器，?為該濾波器所 對應的二值權重。 這里，Rastegari 等人認為單靠二值運算，很難達到原單精度卷積元素的結果，于是他們使用了一個單精度放縮因子?來 對二值濾波器卷積后的結果進行放縮。而??的取值，則可根據優化目標： ? 得到??。二值連接改進的算法訓練過程與之前的算法大致相同，不同的地方在于梯度的計算過程還考慮了??的影響。由于??這個單精度的縮放因子的存在，有效降低了重構誤差，并首次在 ImageNet 數據集上取得了與 Alex-Net 相當的精度。如下圖所示：

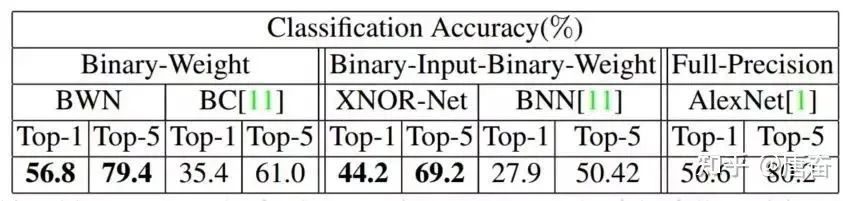
可以看到的是權重二值化神經網絡（BWN）和全精度神經網絡的精確度幾乎一樣，但是與異或神經網絡（XNOR-Net）相比而言，Top-1 和 Top-5 都有 10+% 的損失。

相比于權重二值化神經網絡，異或神經網絡將網絡的輸入也轉化為二進制值，所以，異或神經網絡中的乘法加法 (Multiplication and ACcumulation) 運算用按位異或 (bitwise xnor) 和數 1 的個數 (popcount) 來代替。

更多內容，可以看這兩篇文章： https://github.com/Ewenwan/MVision/tree/master/CNN/Deep_Compression/quantization/BNN https://blog.csdn.net/stdcoutzyx/article/details/50926174

4.4 二值網絡設計注意事項

不要使用 kernel = (1, 1) 的 Convolution （包括 resnet 的 bottleneck）：二值網絡中的 weight 都為 1bit， 如果再是 1x1 大小， 會極大地降低表達能力

增大 Channel 數目 + 增大 activation bit 數 要協同配合：如果一味增大 channel 數， 最終 feature map 因為 bit 數過低， 還是浪費了模型容量。同理反過來也是。

建議使用 4bit 及以下的 activation bit，過高帶來的精度收益變小，而會顯著提高 inference 計算量

5.知識蒸餾

本文只簡單介紹這個領域的開篇之作-Distilling the Knowledge in a Neural Network，這是蒸 "logits"方法，后面還出現了蒸 "features" 的論文。想要更深入理解，中文博客可參考這篇文章-知識蒸餾是什么？一份入門隨筆(https://zhuanlan.zhihu.com/p/90049906)。

知識蒸餾（knowledge distillation）(https://arxiv.org/abs/1503.02531)，是遷移學習（transfer learning）的一種，簡單來說就是訓練一個大模型（teacher）和一個小模型（student），將龐大而復雜的大模型學習到的知識，通過一定技術手段遷移到精簡的小模型上，從而使小模型能夠獲得與大模型相近的性能。 在知識蒸餾的實驗中，我們先訓練好一個 teacher 網絡，然后將 teacher 的網絡的輸出結果??作為 student 網絡的目標，訓練 student 網絡，使得 student 網絡的結果??接近?，因此，student 網絡的損失函數為??。這里??是交叉熵 (Cross Entropy)，?是真實標簽的 onehot 編碼，?是 teacher 網絡的輸出結果，?是 student 網絡的輸出結果。 但是，直接使用 teacher 網絡的 softmax 的輸出結果?，可能不大合適。因此，一個網絡訓練好之后, 對于正確的答案會有一個 很高的置信度。例如，在 MNIST 數據中，對于某個 2 的輸入，對于 2 的預測概率會很高，而對于 2 類似的數字，例如 3 和 7 的預測概率為??和??。這樣的話，teacher 網絡學到數據的相似信息（例如數字 2 和 3，7 很類似）很難傳達給 student 網絡，因為它們的概率值接近0。因此，論文提出了 softmax-T(軟標簽計算公式)公式，如下所示： ? 這里??是 student 網絡學習的對象（soft targets) ，?是 teacher 網絡 softmax 前一層的輸出 logit。如果將??取 1，上述公式變成?，根據 logit 輸出各個類別的概率。如果??接近于 0，則最大的值會越近 1 ，其它值會接近 0，近似于 onehot 編碼。 所以，可以知道 student 模型最終的損失函數由兩部分組成：

第一項是由小模型(student 模型)的預測結果與大模型的“軟標簽”所構成的交叉熵（cross entroy）;

第二項為小模型預測結果與普通類別標簽的交叉熵。

這兩個損失函數的重要程度可通過一定的權重進行調節，在實際應用中， T 的取值會影響最終的結果，一般而言，較大的 T 能夠獲得較高的準確度，T（蒸餾溫度參數） 屬于知識蒸餾模型訓練超參數的一種。T 是一個可調節的超參數、T 值越大、概率分布越軟（論文中的描述），曲線便越平滑，相當于在遷移學習的過程中添加了擾動，從而使得學生網絡在借鑒學習的時候更有效、泛化能力更強，這其實就是一種抑制過擬合的策略。知識蒸餾的整個過程如下圖：

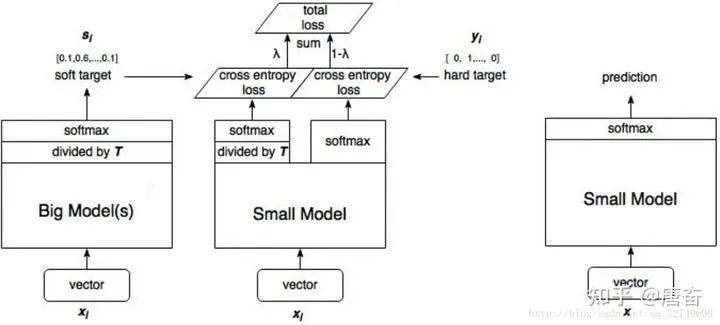
student 模型的實際模型結構和小模型一樣，但是損失函數包含了兩部分，分類網絡的知識蒸餾 mxnet 代碼示例如下：

?

#?-*-coding-*-??:?utf-8?? """ 本程序沒有給出具體的模型結構代碼，主要給出了知識蒸餾 softmax 損失計算部分。
""" import?mxnet?as?mx def?get_symbol(data,?class_labels,?resnet_layer_num,Temperature,mimic_weight,num_classes=2): ????
backbone?=?StudentBackbone(data)??#?Backbone?為分類網絡?backbone?類 ??
??flatten?=?mx.symbol.Flatten(data=conv1,?name="flatten") ??
??fc_class_score_s?=?mx.symbol.FullyConnected(data=flatten,?num_hidden=num_classes,?name='fc_class_score') ???
softmax1?=?mx.symbol.SoftmaxOutput(data=fc_class_score_s,?label=class_labels,?name='softmax_hard')
????import?symbol_resnet??#?Teacher?model ?
???fc_class_score_t?=?symbol_resnet.get_symbol(net_depth=resnet_layer_num,?num_class=num_classes,?data=data) ?
???s_input_for_softmax=fc_class_score_s/Temperature ?
???t_input_for_softmax=fc_class_score_t/Temperature ??
??t_soft_labels=mx.symbol.softmax(t_input_for_softmax,?name='teacher_soft_labels') ??
??softmax2?=?mx.symbol.SoftmaxOutput(data=s_input_for_softmax,?label=t_soft_labels,?name='softmax_soft',grad_scale=mimic_weight) ??
??group=mx.symbol.Group([softmax1,softmax2]) ?
???group.save('group2-symbol.json') ?
???return?group tensorflow代碼示例如下：

#?將類別標簽進行one-hot編碼 one_hot?=?tf.one_hot(y,?n_classes,1.0,0.0)?#?n_classes為類別總數,?n為類別標簽 #?one_hot?=?tf.cast(one_hot_int,?tf.float32) teacher_tau?=?tf.scalar_mul(1.0/args.tau,?teacher)?#?teacher為teacher模型直接輸出張量,?tau為溫度系數T student_tau?=?tf.scalar_mul(1.0/args.tau,?student)?#?將模型直接輸出logits張量student處于溫度系數T objective1?=?tf.nn.sigmoid_cross_entropy_with_logits(student_tau,?one_hot) objective2?=?tf.scalar_mul(0.5,?tf.square(student_tau-teacher_tau)) """
student模型最終的損失函數由兩部分組成： 第一項是由小模型的預測結果與大模型的“軟標簽”所構成的交叉熵（cross?entroy）; 第二項為預測結果與普通類別標簽的交叉熵。 """ tf_loss?=?(args.lamda*tf.reduce_sum(objective1)?+?(1-args.lamda)*tf.reduce_sum(objective2))/batch_size tf.scalar_mul 函數為對 tf 張量進行固定倍率 scalar 縮放函數。一般 T 的取值在 1 - 20 之間，這里我參考了開源代碼，取值為 3。我發現在開源代碼中 student 模型的訓練，有些是和 teacher 模型一起訓練的，有些是 teacher 模型訓練好后直接指導 student 模型訓練。

6. 淺層/輕量網絡

淺層網絡：通過設計一個更淺（層數較少）結構更緊湊的網絡來實現對復雜模型效果的逼近, 但是淺層網絡的表達能力很難與深層網絡相匹敵。因此，這種設計方法的局限性在于只能應用解決在較為簡單問題上。如分類問題中類別數較少的 task。 輕量網絡：使用如 MobilenetV2、ShuffleNetv2 等輕量網絡結構作為模型的 backbone可以大幅減少模型參數數量。

參考資料

https://www.cnblogs.com/dyl222/p/11079489.html

https://github.com/chengshengchan/model_compression/blob/master/teacher-student.py

https://github.com/dkozlov/awesome-knowledge-distillation

https://arxiv.org/abs/1603.05279

解析卷積神經網絡-深度學習實踐手冊

https://zhuanlan.zhihu.com/p/81467832

編輯：黃飛

?