在機(jī)器學(xué)習(xí)和相關(guān)領(lǐng)域，人工神經(jīng)網(wǎng)絡(luò)的計(jì)算模型靈感正是來(lái)自生物神經(jīng)網(wǎng)絡(luò)：每個(gè)神經(jīng)元與其他神經(jīng)元相連，當(dāng)它興奮時(shí)，就會(huì)像相鄰的神經(jīng)元發(fā)送化學(xué)物質(zhì)，從而改變這些神經(jīng)元內(nèi)的電位；如果某神經(jīng)元的電位超過(guò)了一個(gè)閾值，那么它就會(huì)被激活（興奮），向其他神經(jīng)元發(fā)送化學(xué)物質(zhì)。人工神經(jīng)網(wǎng)絡(luò)通常呈現(xiàn)為按照一定的層次結(jié)構(gòu)連接起來(lái)的“神經(jīng)元”，它可以從輸入的計(jì)算值，進(jìn)行分布式并行信息處理的算法數(shù)學(xué)模型。這種網(wǎng)絡(luò)依靠系統(tǒng)的復(fù)雜程度，通過(guò)調(diào)整內(nèi)部大量節(jié)點(diǎn)之間相互連接的關(guān)系，從而達(dá)到處理信息的目的。并且它也被用于估計(jì)或可以依賴于大量的輸入和一般的未知近似函數(shù)，來(lái)最大化的擬合現(xiàn)實(shí)中的實(shí)際數(shù)據(jù)，提高機(jī)器學(xué)習(xí)預(yù)測(cè)的精度。

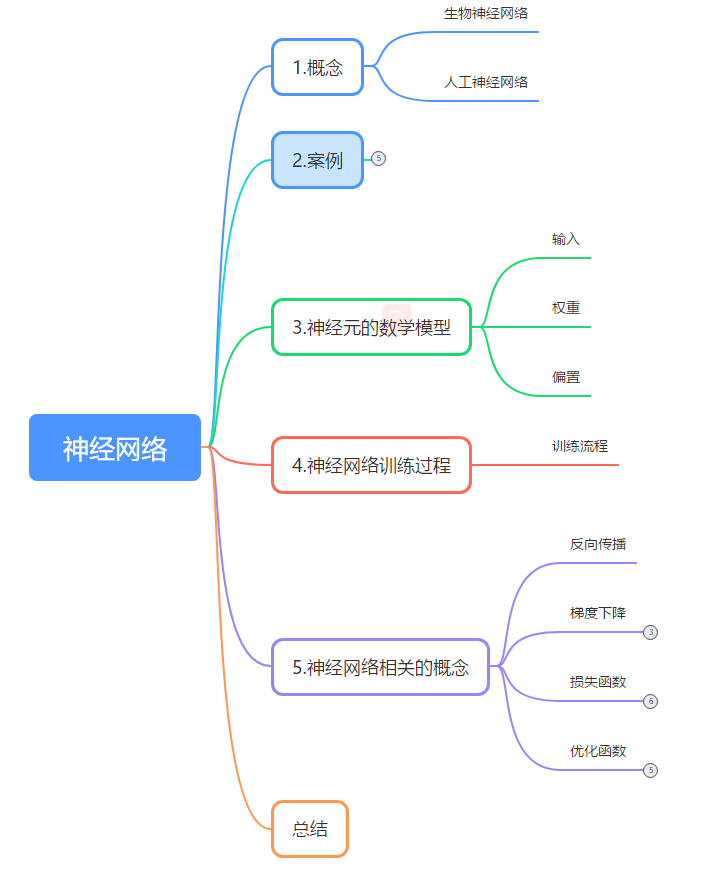
概要

單純的講神經(jīng)網(wǎng)絡(luò)的概念有些抽象，先通過(guò)一個(gè)實(shí)例展示一下機(jī)器學(xué)習(xí)中的神經(jīng)網(wǎng)絡(luò)進(jìn)行數(shù)據(jù)處理的完整過(guò)程。

01神經(jīng)網(wǎng)絡(luò)的實(shí)例

1.1 案例介紹

實(shí)例：訓(xùn)練一個(gè)神經(jīng)網(wǎng)絡(luò)模型擬合 廣告投入（TV,radio,newspaper 3種方式）和銷售產(chǎn)出的關(guān)系，實(shí)現(xiàn)根據(jù)廣告投放來(lái)預(yù)測(cè)銷售情況。

樣本數(shù)據(jù)：參考下圖

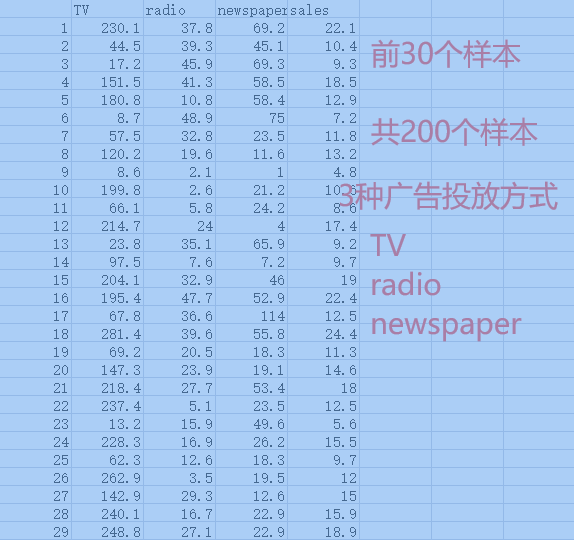
樣本數(shù)據(jù)

TV，radio和newspaper是樣本數(shù)據(jù)的3個(gè)特征，sales是樣本標(biāo)簽。

1.2 準(zhǔn)備數(shù)據(jù)

?

#添加引用
import tensorflow as tf
import pandas as pd
import numpy as np
#加載數(shù)據(jù)
data = pd.read_csv('../dataset/Advertising.csv')#pd 是數(shù)據(jù)分析庫(kù)pandas
# 建立模型 根據(jù)tv，廣播，報(bào)紙投放額 預(yù)測(cè)銷量
print(type(data),data.shape)### (200, 5)
#取特征 x取值除去第一列和最后一列的值取出所有投放廣告的值
x = data.iloc[:,1:-1]#200*3
#y取值最后一列銷量的值 標(biāo)簽
y = data.iloc[:,-1] #200*1

?

1.3 構(gòu)建一個(gè)神經(jīng)網(wǎng)絡(luò)

建立順序模型：Sequential

隱藏層：一個(gè)多層感知器(隱含層10層Dense(10),形狀input_shape=(3,)，對(duì)應(yīng)樣本的3個(gè)特征列,激活函數(shù)activation="relu")，

輸出層：標(biāo)簽是一個(gè)預(yù)測(cè)值，緯度是1

?

model = tf.keras.Sequential([tf.keras.layers.Dense(10,input_shape=(3,),activation="relu"),
tf.keras.layers.Dense(1)])

?

模型結(jié)構(gòu) print(model.summary())

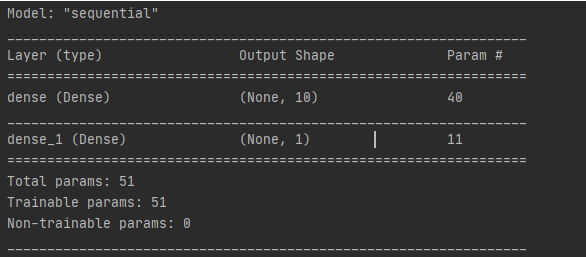
模型結(jié)構(gòu)

說(shuō)明：

1）keras的模型，Sequential表示順序模型，因?yàn)槭侨B接的，選擇順序模型

2）tf.keras.layers.Dense 是添加網(wǎng)絡(luò)層數(shù)的API

3）隱藏層參數(shù) 40個(gè)，10個(gè)感知器（神經(jīng)元），每個(gè)感知器有4個(gè)參數(shù)（w1,w2,w3,b），總共10*4 = 40

4）輸出層參數(shù)11個(gè)，1個(gè)感知器（神經(jīng)元），參數(shù)(w1,w2,w3,w4,w5,w6,w7,w8,w9,w10,b)共11個(gè)

5）模型參數(shù)個(gè)數(shù)總計(jì)40+11 = 51個(gè)

1.4 給創(chuàng)建的模型加入優(yōu)化器和損失函數(shù)

# 優(yōu)化器adam，線性回歸模型損失函數(shù)為均方差（mse）

model.compile(optimizer="adam",loss="mse")

1.5啟動(dòng)訓(xùn)練

# 訓(xùn)練模型

model.fit(x,y,epochs=100)

x 是樣本的特征；y 是樣本的標(biāo)簽

epochs?是梯度下降中的概念，當(dāng)一個(gè)完整的數(shù)據(jù)集通過(guò)了神經(jīng)網(wǎng)絡(luò)一次并且返回了一次，這個(gè)過(guò)程稱為一個(gè)?epoch；當(dāng)一個(gè) epoch 對(duì)于計(jì)算機(jī)而言太龐大的時(shí)候，就需要把它分成多個(gè)小塊，需要設(shè)置batch_size,這部分內(nèi)容在后面的梯度下降章節(jié)再詳細(xì)介紹。

1.6使用模型預(yù)測(cè)

# 使用該模型在現(xiàn)有數(shù)據(jù)上預(yù)測(cè)前10個(gè)樣本的銷量

test = data.iloc[:10,1:-1]

print('測(cè)試值',model.predict(test))

以上步驟展示一個(gè)神經(jīng)網(wǎng)絡(luò)模型的構(gòu)建，訓(xùn)練和預(yù)測(cè)的全部過(guò)程，下面再介紹一下原理。

02神經(jīng)元的數(shù)學(xué)模型

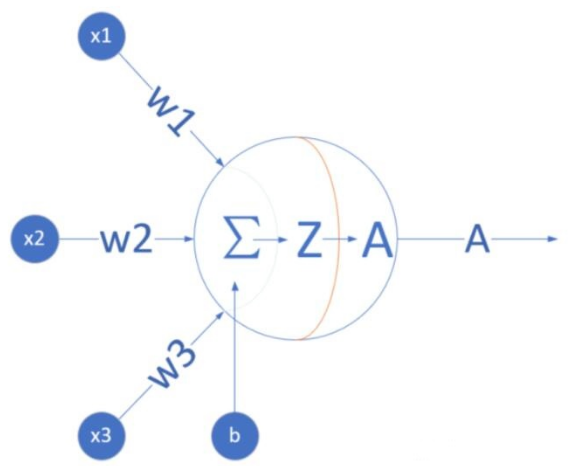
神經(jīng)元的數(shù)學(xué)模型

輸入 input

(x1, x2, x3) 是外界輸入信號(hào)，一般是一個(gè)訓(xùn)練數(shù)據(jù)樣本的多個(gè)屬性/特征，可以理解為實(shí)例中的3種廣告投放方式。

權(quán)重 weights

(w1,w2,w3) 是每個(gè)輸入信號(hào)的權(quán)重值，以上面的 (x1,x2,x3)的例子來(lái)說(shuō)，x1的權(quán)重可能是 0.92，x2的權(quán)重可能是 0.2，x3的權(quán)重可能是 0.03。當(dāng)然權(quán)重值相加之后可以不是 1。

偏移bias

還有個(gè) b 是怎么來(lái)的？一般的書或者博客上會(huì)告訴你那是因?yàn)?y=wx+by，b 是偏移值，使得直線能夠沿 Y軸上下移動(dòng)。從生物學(xué)上解釋，在腦神經(jīng)細(xì)胞中，一定是輸入信號(hào)的電平/電流大于某個(gè)臨界值時(shí)，神經(jīng)元細(xì)胞才會(huì)處于興奮狀態(tài)，這個(gè) b 實(shí)際就是那個(gè)臨界值。亦即當(dāng)：w1*x1+w2*x2+w3*x3>=t?時(shí),該神經(jīng)元細(xì)胞才會(huì)興奮。我們把t挪到等式左側(cè)來(lái)，變成(?t)，然后把它寫成 b，變成了：w1*x1+w2*x2+w3*x3+b>=0

03神經(jīng)網(wǎng)絡(luò)訓(xùn)練過(guò)程

還是以前面的廣告投放為例，神經(jīng)網(wǎng)絡(luò)訓(xùn)練之前需要先搭建一個(gè)網(wǎng)絡(luò)，然后填充數(shù)據(jù)（加入含特征和標(biāo)簽的樣本數(shù)據(jù)）訓(xùn)練，訓(xùn)練的過(guò)程就是不斷更新權(quán)重w和偏置b的過(guò)程。輸入有10層，每一層的特征個(gè)數(shù)由樣本確定（實(shí)例中的3種廣告投放方式即3個(gè)特征列），每一層參數(shù)就有4個(gè)（w1,w2,w3,b），全連接時(shí)10層相當(dāng)于10*4=40 個(gè)參數(shù)。如下是一個(gè)單層神經(jīng)網(wǎng)絡(luò)模型，但是有2個(gè)神經(jīng)元。

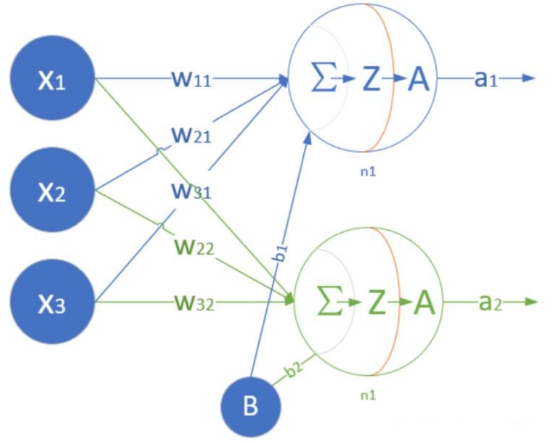
2個(gè)神經(jīng)元的模型

訓(xùn)練流程

訓(xùn)練的過(guò)程就是不斷更新權(quán)重w和偏置b的過(guò)程，直到找到穩(wěn)定的w和b 使得模型的整體誤差最小。具體的流程如下，

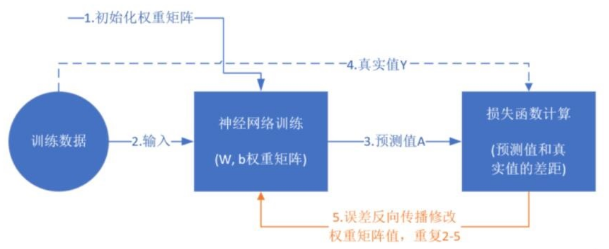
訓(xùn)練過(guò)程示意圖

04神經(jīng)網(wǎng)絡(luò)相關(guān)的概念

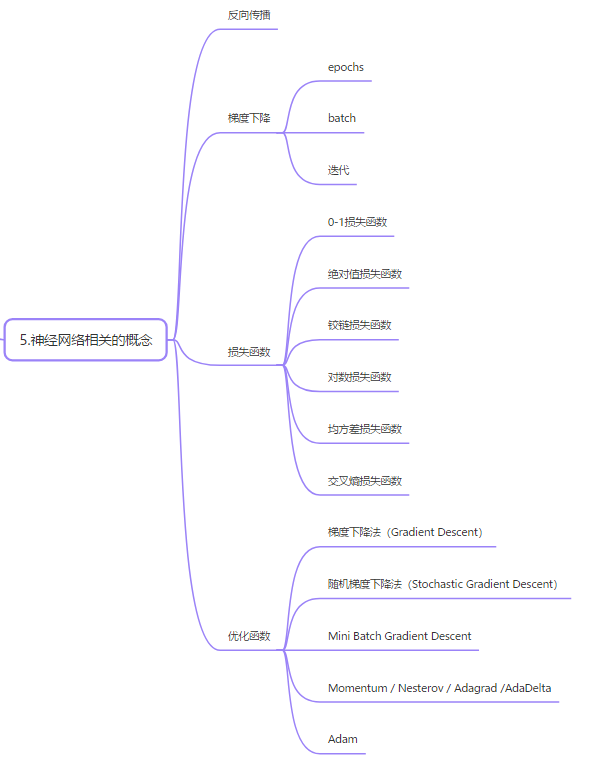
4.1反向傳播

反向傳播算法是一種高效計(jì)算數(shù)據(jù)流圖中梯度的技術(shù)，每一層的導(dǎo)數(shù)都是后一層的導(dǎo)數(shù)與前一層輸出之積，這正是鏈?zhǔn)椒▌t的奇妙之處，誤差反向傳播算法利用的正是這一特點(diǎn)。

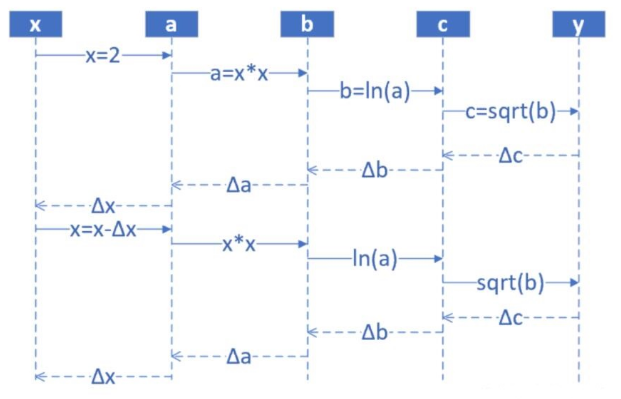
反向傳播算法示意圖

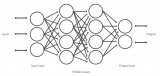
前饋時(shí)，從輸入開始，逐一計(jì)算每個(gè)隱含層的輸出，直到輸出層。

正向過(guò)程

step1，輸入層，隨機(jī)輸入第一個(gè) x值，x 的取值范圍 (1,10]，假設(shè)x是 2；

step2，第一層網(wǎng)絡(luò)計(jì)算，接收step1傳入 x 的值，計(jì)算：a=x^2；

step3，第二層網(wǎng)絡(luò)計(jì)算，接收step2傳入 a 的值，計(jì)算：b=ln (a)；

step4，第三層網(wǎng)絡(luò)計(jì)算，接收step3傳入 b 的值，計(jì)算：c=sqrt{b}；

step5，輸出層，接收step4傳入 c 的值

然后開始計(jì)算導(dǎo)數(shù)，并從輸出層經(jīng)各隱含層逐一反向傳播。為了減少計(jì)算量，還需對(duì)所有已完成計(jì)算的元素進(jìn)行復(fù)用。

反向過(guò)程

反向傳播 --- 每一層的導(dǎo)數(shù)都是后一層的導(dǎo)數(shù)與前一層輸出之積

step6，計(jì)算y與c的差值：Δc = c-y,傳回step4

step7，step4 接收step5傳回的Δc，計(jì)算Δb = Δc*2sqrt(b)

step8，step3 接收step4傳回的Δb，計(jì)算Δa = Δb*a

step9，step2 接收step3傳回的Δa，計(jì)算Δx = Δ/(2*x)

step10，step1 接收step2傳回的Δx，更新x(x-Δx),回到step1,從輸入層開始下一輪循環(huán)

4.2.梯度下降

梯度下降是一個(gè)在機(jī)器學(xué)習(xí)中用于尋找最佳結(jié)果（曲線的最小值）的迭代優(yōu)化算法，它包含了如下2層含義：

梯度：函數(shù)當(dāng)前位置的最快上升點(diǎn)；

下降：與倒數(shù)相反的方向，用數(shù)學(xué)語(yǔ)言描述的就是那個(gè)減號(hào)，亦即與上升相反的方向運(yùn)動(dòng)，就是下降，代價(jià)函數(shù)減小。

梯度下降數(shù)學(xué)公式

其中：

θ(n+1)：下一個(gè)值

θ(n):當(dāng)前值

-：減號(hào)，梯度的反向，

η：學(xué)習(xí)率或步長(zhǎng)，控制每一步走的距離，不要太快，避免錯(cuò)過(guò)了極值點(diǎn)；也不要太慢，以免收斂時(shí)間過(guò)長(zhǎng)

▽：梯度 ，函數(shù)當(dāng)前位置的最快上升點(diǎn)

J(θ):函數(shù)

梯度下降算法是迭代的，意思是需要多次使用算法獲取結(jié)果，以得到最優(yōu)化結(jié)果。梯度下降的迭代性質(zhì)能使欠擬合的圖示演化以獲得對(duì)數(shù)據(jù)的最佳擬合。

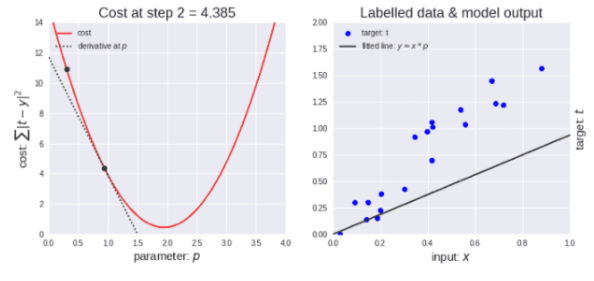
梯度下降算法示意圖

如上圖左所示，剛開始學(xué)習(xí)率很大，因此下降步長(zhǎng)更大。隨著點(diǎn)下降，學(xué)習(xí)率變得越來(lái)越小，從而下降步長(zhǎng)也變小。同時(shí)，代價(jià)函數(shù)也在減小，或者說(shuō)代價(jià)在減小，有時(shí)候也稱為損失函數(shù)或者損失，兩者都是一樣的。

在一般情況下，一次性將數(shù)據(jù)輸入計(jì)算機(jī)是不可能的。因此，為了解決這個(gè)問(wèn)題，我們需要把數(shù)據(jù)分成小塊，一塊一塊地傳遞給計(jì)算機(jī)，在每一步的末端更新神經(jīng)網(wǎng)絡(luò)的權(quán)重，擬合給定的數(shù)據(jù)。這樣就需要了解?epochs，batch size?這些概念。

epochs

當(dāng)一個(gè)完整的數(shù)據(jù)集通過(guò)了神經(jīng)網(wǎng)絡(luò)一次并且返回了一次，這個(gè)過(guò)程稱為一個(gè)?epoch。然而，當(dāng)一個(gè)?epoch?對(duì)于計(jì)算機(jī)而言太龐大的時(shí)候，就需要把它分成多個(gè)小塊。

設(shè)置epoch 的個(gè)數(shù)

完整的數(shù)據(jù)集在同樣的神經(jīng)網(wǎng)絡(luò)中傳遞多次。但是請(qǐng)記住，我們使用的是有限的數(shù)據(jù)集，并且我們使用一個(gè)迭代過(guò)程即梯度下降，優(yōu)化學(xué)習(xí)過(guò)程和圖示。因此僅僅更新權(quán)重一次或者說(shuō)使用一個(gè) epoch 是不夠的。

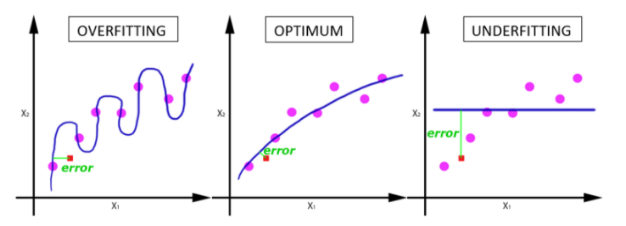
在神經(jīng)網(wǎng)絡(luò)中傳遞完整的數(shù)據(jù)集一次是不夠的，而且我們需要將隨著 epoch 數(shù)量增加，神經(jīng)網(wǎng)絡(luò)中的權(quán)重的更新次數(shù)也增加，曲線從欠擬合變得過(guò)擬合。那么，幾個(gè) epoch 才是合適的呢？呵呵，這個(gè)問(wèn)題并沒(méi)有確定的標(biāo)準(zhǔn)答案，需要開發(fā)者根據(jù)數(shù)據(jù)集的特性和個(gè)人經(jīng)驗(yàn)來(lái)設(shè)置。

batch

在不能將數(shù)據(jù)一次性通過(guò)神經(jīng)網(wǎng)絡(luò)的時(shí)候，就需要將數(shù)據(jù)集分成幾個(gè)?batch。

迭代

迭代是?batch?需要完成一個(gè) epoch 的次數(shù)。記住：在一個(gè) epoch 中，batch 數(shù)和迭代數(shù)是相等的。

比如對(duì)于一個(gè)有 2000 個(gè)訓(xùn)練樣本的數(shù)據(jù)集。將 2000 個(gè)樣本分成大小為 400 的 batch（5個(gè)batch），那么完成一個(gè) epoch 需要 5次迭代。

4.3 損失函數(shù)

“損失”就是所有樣本的“誤差”的總和，亦即（mm 為樣本數(shù)）：

損失函數(shù)表達(dá)式

（1）0-1損失函數(shù)

（2）絕對(duì)值損失函數(shù)

（3）鉸鏈損失函數(shù)

（4）對(duì)數(shù)損失函數(shù)

（5）均方差損失函數(shù)

（6）交叉熵?fù)p失函數(shù)

均方差和交叉熵表達(dá)式

4.優(yōu)化函數(shù)

實(shí)例中的第1.4節(jié)，給創(chuàng)建的模型加入優(yōu)化器和損失函數(shù)

?

# 優(yōu)化器adam，線性回歸模型損失函數(shù)為均方差（mse）
model.compile(optimizer="adam",loss="mse")

?

這里使用的是adam優(yōu)化器，在神經(jīng)網(wǎng)絡(luò)中，優(yōu)化方法還有很多，這里選擇幾種做個(gè)簡(jiǎn)單介紹，詳細(xì)信息還需要單獨(dú)去查找資料。

1)梯度下降法（Gradient Descent）

梯度下降法是最重要的一種方法，也是很多其他優(yōu)化算法的基礎(chǔ)。

2)隨機(jī)梯度下降法（Stochastic Gradient Descent）

每次只用一個(gè)樣本進(jìn)行更新，計(jì)算量小，更新頻率高；容易導(dǎo)致模型超調(diào)不穩(wěn)定，收斂也不穩(wěn)定

3)Mini Batch Gradient Descent

mini batch 梯度下降法是梯度下降法和隨機(jī)梯度下降法的折衷，即在計(jì)算loss的時(shí)候，既不是直接計(jì)算整個(gè)數(shù)據(jù)集的loss，也不是只計(jì)算一個(gè)樣本的loss，而是計(jì)算一個(gè)batch的loss，batch的大小自己設(shè)定。

4)Momentum

帶momentum(動(dòng)量)的梯度下降法也是一種很常用的的優(yōu)化算法。這種方法因?yàn)橐肓薽omentum量，所以能夠?qū)μ荻认陆捣ㄆ鸬郊铀俚淖饔谩?/p>

5)Nesterov

NAG算法簡(jiǎn)而言之，就是在進(jìn)行Momentum梯度下降法之前，先做一個(gè)預(yù)演，看看沿著以前的方向進(jìn)行更新是否合適，不合適就立馬調(diào)整方向。也就是說(shuō)參數(shù)更新的方向不再是當(dāng)前的梯度方向，而是參數(shù)未來(lái)所要去的真正方向。

6)Adagrad

在訓(xùn)練過(guò)程中，每個(gè)不參數(shù)都有自己的學(xué)習(xí)率，并且這個(gè)學(xué)習(xí)率會(huì)根據(jù)自己以前的梯度平方和而進(jìn)行衰減。

優(yōu)點(diǎn)：在訓(xùn)練的過(guò)程中不用人為地調(diào)整學(xué)習(xí)率，一般設(shè)置好默認(rèn)的初始學(xué)習(xí)率就行了

缺點(diǎn)：隨著迭代的進(jìn)行，公式（6）中的學(xué)習(xí)率部分會(huì)因?yàn)榉帜钢饾u變大而變得越來(lái)越小，在訓(xùn)練后期模型幾乎不再更新參數(shù)。

7)AdaDelta

AdaDelta是Adagrad的改進(jìn)版，目的就是解決Adagrad在訓(xùn)練的后期，學(xué)習(xí)率變得非常小，降低模型收斂速度。

8)Adam

這里重點(diǎn)介紹一下Adam

前面我們從最經(jīng)典的梯度下降法開始，介紹了幾個(gè)改進(jìn)版的梯度下降法。

Momentum方法通過(guò)添加動(dòng)量，提高收斂速度；

Nesterov方法在進(jìn)行當(dāng)前更新前，先進(jìn)行一次預(yù)演，從而找到一個(gè)更加適合當(dāng)前情況的梯度方向和幅度；

Adagrad讓不同的參數(shù)擁有不同的學(xué)習(xí)率，并且通過(guò)引入梯度的平方和作為衰減項(xiàng)，而在訓(xùn)練過(guò)程中自動(dòng)降低學(xué)習(xí)率；

AdaDelta則對(duì)Adagrad進(jìn)行改進(jìn)，讓模型在訓(xùn)練后期也能夠有較為適合的學(xué)習(xí)率。

既然不同的參數(shù)可以有不同的學(xué)習(xí)率，那么不同的參數(shù)是不是也可以有不同的Momentum呢？

Adam方法就是根據(jù)上述思想而提出的，對(duì)于每個(gè)參數(shù)，其不僅僅有自己的學(xué)習(xí)率，還有自己的Momentum量，這樣在訓(xùn)練的過(guò)程中，每個(gè)參數(shù)的更新都更加具有獨(dú)立性，提升了模型訓(xùn)練速度和訓(xùn)練的穩(wěn)定性。

Adam（Adaptive Moment Estimation）：

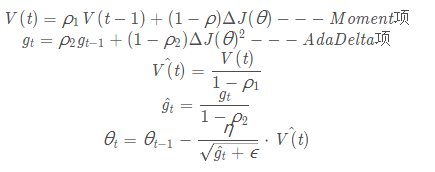
一般的，ρ 1 設(shè)置為0.9， ρ 2 設(shè)置為0.999

套用別人說(shuō)過(guò)的一句話：

Adam works well in practice and outperforms other Adaptive techniques.

事實(shí)上，如果你的數(shù)據(jù)比較稀疏，那么像SGD，NAG以及Momentum的方法往往會(huì)表現(xiàn)得比較差，這是因?yàn)閷?duì)于模型中的不同參數(shù)，他們均使用相同的學(xué)習(xí)率，這會(huì)導(dǎo)致那些應(yīng)該更新快的參數(shù)更新的慢，而應(yīng)該更新慢的有時(shí)候又會(huì)因?yàn)閿?shù)據(jù)的原因的變得快。因此，對(duì)于稀疏的數(shù)據(jù)更應(yīng)該使用Adaptive方法（Adagrad、AdaDelta、Adam）。同樣，對(duì)于一些深度神經(jīng)網(wǎng)絡(luò)或者非常復(fù)雜的神經(jīng)網(wǎng)絡(luò)，使用Adam或者其他的自適應(yīng)（Adaptive）的方法也能夠更快的收斂。

05總結(jié)

回顧一下本文的主要內(nèi)容：

1）理解概念：人工神經(jīng)網(wǎng)絡(luò)靈感來(lái)自于生物神經(jīng)網(wǎng)絡(luò)，它可以通過(guò)增加隱層神經(jīng)元的數(shù)量，按照任意給定的精度近似任何連續(xù)函數(shù)來(lái)提升模型近似的精度。

2）實(shí)例介紹了構(gòu)建人工神經(jīng)網(wǎng)絡(luò)模型的機(jī)器學(xué)習(xí)實(shí)現(xiàn)過(guò)程

3）人工神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過(guò)程

4）詳細(xì)介紹了神經(jīng)網(wǎng)絡(luò)相關(guān)的一些基本概念：反向傳播，梯度下降，損失函數(shù)，優(yōu)化函數(shù)，epoch,batch size ,優(yōu)化器，學(xué)習(xí)率等

審核編輯：湯梓紅