圖像縮放是數字圖像處理中常用的技術之一。隨著數字媒體的普及,圖像縮放算法變得越來越重要。本文將探討圖像縮放的原理,著重介紹兩種常用的插值算法——最近鄰插值和雙線性插值,并提供對應的代碼實現。我們將解釋這些算法的工作原理,以及如何選擇最適合您應用場景的算法。 ? 開發中可能非專業的開發人員外,其他人不會對其涉獵,但是圖像的縮放這個話題確實值得我們學習和研究。 ? 圖像包含圖片和視頻,當你看視頻時全屏變小窗,小窗變大屏等都用到了圖像縮放,就視頻而言,不同分辨率的切換也用到了縮放算法,比如,電影分辨率是 1080P,播放器的窗口大小是720P,則需要將電影畫面從1080P縮小到720P再播放。如果你點擊全屏播放,播放窗口變成了4K,則需要將電影畫面做放大處理,即放大到4K之后再播放。 ?
那圖像縮放算法都有哪些呢?
他們的原理是什么?
在Android開發中怎么使用
圖像縮放算法
圖像縮放算法可以分為兩類:插值算法和基于變換的算法。下面是一些常見的圖像縮放算法: ?
最近鄰插值算法(Nearest Neighbor Interpolation):最簡單的插值算法,對于每個縮放后的像素點,選擇與其最近的原始像素點的值作為它的值。該算法容易實現,但會導致圖像出現鋸齒狀的邊緣。
雙線性插值算法(Bilinear Interpolation):該算法在最近鄰插值算法的基礎上,加入了對相鄰四個像素點的加權平均,使得圖像邊緣更加平滑。
雙三次插值算法(Bicubic Interpolation):該算法在雙線性插值算法的基礎上,對相鄰16個像素點進行加權平均,得到更加平滑的圖像。
Lanczos插值算法(LanczosInterpolation):該算法使用了一種卷積方法,通過對像素點周圍的采樣點進行加權平均,得到縮放后像素點的值。該算法在保持圖像細節的同時,會對圖像進行輕微模糊。
Sinc插值算法(SincInterpolation):該算法基于信號處理中的Sinc函數,使用卷積方法對像素點進行加權平均。該算法在保持圖像細節的同時,會對圖像進行一定的模糊,但比Lanczos插值算法的模糊程度小。
基于變換的算法:除了插值算法,還有一些基于變換的算法,如雙線性變換、雙三次變換、圖像金字塔等。這些算法會對原始圖像進行一定的變換,再進行縮放。這些算法通常能夠產生更高質量的縮放結果,但計算復雜度也更高。
這些算法已經在行業中有較多的資料和使用文獻,我這里簡單梳理一下他們的原理以及在Android中怎么使用這些算法。 ?
縮放的原理
? 首先要明確一點就是圖像的縮放就是將原圖像的已有像素經過加權運算得到目標圖像的目標像素。比如說,我們已有圖像是720P的分辨率,稱之為原圖像,我們需要放大到1080P,我們稱這個1080P圖像是目標圖像。目標圖像在寬度方向上放大了1920 / 1280 = 1.5倍,高度方向上也放大了1080 / 720 = 1.5倍。 ? 那怎么通過720的圖像生成1080的圖像呢?放大之后會不會存在間隙,這個間隙是否會導致圖像“發虛”呢? ? 做法如下: ? 先將目標圖像的像素位置映射到原圖像的對應位置上,然后把通過插值計算得到的原圖像對應位置的像素值作為目標圖像相應位置的像素值。 ? 這樣操作之后是不是就沒有間隙了。這就是插值算法要干的事了。1080P目標圖像中的(0,0)位置就映射到720P原圖像的(0,0)位置,取原圖像(0,0)位置的像素值作為目標圖像(0,0)位置的像素值。目標圖像的(1,1)位置就映射到原圖像中的(0.67,0.67)位置。最后,通過原圖像已有像素插值得到(0.67,0.67)位置的像素值,并將該像素值作為目標圖像(1,1)位置的像素值。下圖中,顯示了720p放大到1080p的圖示和720p縮小到360p的圖示。 ?
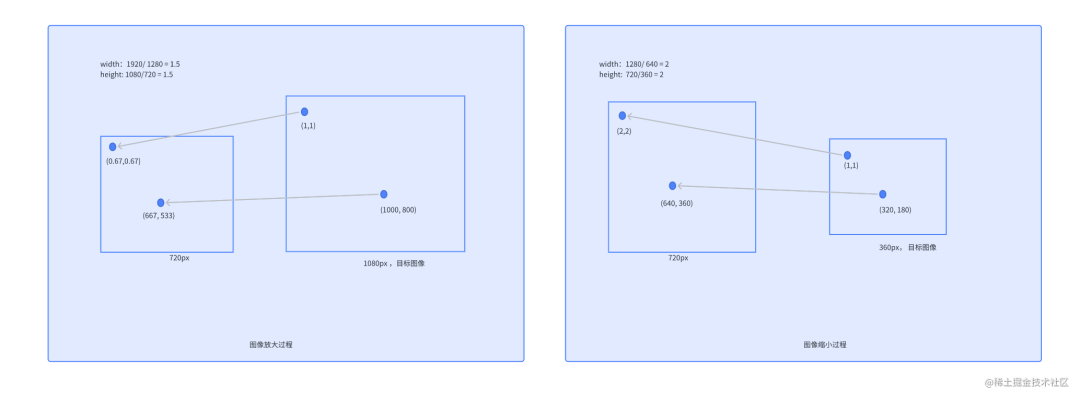
? 通過這個演示,可以總結一下圖像縮放的一般過程: ?
放大過程對于1080P目標圖像中的每一個像素點(x,y),我們只需要將它映射到 720P原圖像的(x / 1.5,y / 1.5)位置,通過原圖像已有的像素值插值得到(x / 1.5,y / 1.5)的像素值就可以了。
縮小過程對于360P目標圖像中的每一個像素點(x,y),我們只需要將它映射到720P原圖像的(x * 2,y * 2)位置,通過原圖像已有的像素值插值得到(x * 2,y * 2)的像素值就可以了。
然后二者的操作過程是,遍歷一下目標圖像中的每一個像素點位置,都能找到他們在原圖像中的映射位置,并通過插值求出映射位置的像素值,這樣就可以得到目標圖像了 ? 我們可以推測出,縮放的代碼邏輯是: ?
獲取目標圖像的寬高;
然后獲取獲取像素,完成像素插值
將處理過的像素創建新的圖像
不用著急,后面可以驗證該推測。 ? 縮放的通用表達式 ? 假設原圖像的分辨率是 w0 x h0,我們需要縮放到 w1 x h1。那我們只需要將目標圖像中的像素位置(x,y)映射到原圖像的(x * w0 / w1,y * h0 / h1),再插值得到這個像素值就可以了,這個插值得到的像素值就是目標圖像像素點(x,y)的像素值。注意,(x * w0 / w1,y * h0 / h1)絕大多數時候是小數。這就是圖像縮放算法原理的通用表達示圖如下: ?
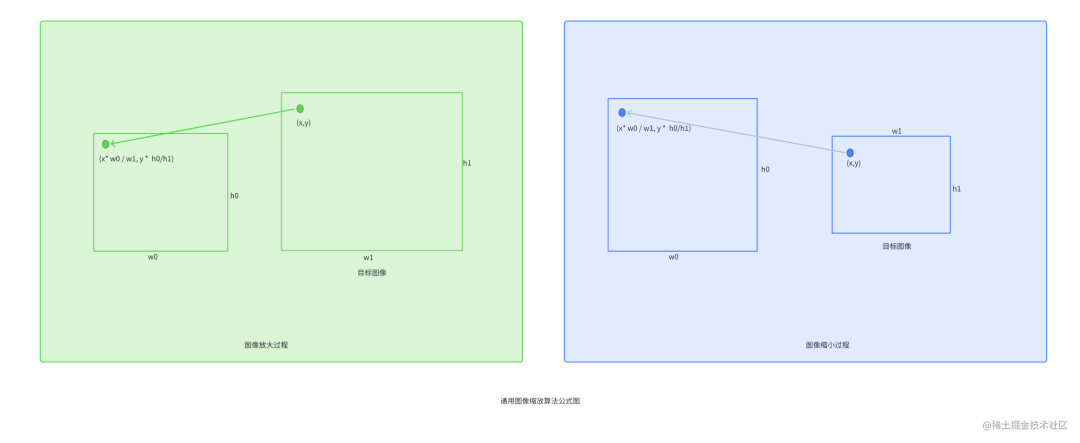
? 目前比較流行的插值算法基本有三種。 ? ?
插值算法
最近鄰插值算法 ? 最近鄰插值算法是一種基本的圖像插值算法,它的基本思想是對于待插值像素的位置,選擇距離該位置最近的一個已知像素值作為插值結果。因此,該算法得名為“最近鄰插值”。 ? 最近鄰插值算法的具體實現過程如下: ?
確定待插值像素位置,假設其坐標為(x,y)。
找到離(x,y)最近的已知像素,假設其坐標為(x1,y1)。
將該已知像素的像素值賦值給待插值像素。
還是看圖像從720p放大到1080p,這個例子,我們上面說了縮放的原理就是映射像素,即將目標圖像的像素映射到原圖像。 ? 1080p假設(2,2)的位置,最鄰近插值法的取值過程是: ? 映射到720P圖像,映射位置是(2 * 1280 / 1920,2 * 720 / 1080),也就是(1.33,1.33)位置,其周圍4個像素分別是(1,1)、(1,2)、(2,1)和(2,2),很明顯(1,1)離(1.33l,1.33)位置最近,那我們取原圖像(1,1)的像素值賦值給1080P圖像的(2,2)位置的像素點。 ?

? 左圖為放大過程,右圖為放大時取值圖示: ?
所以1080待插值的位置(2,2)
找到了離(2,2)最近的已知像素(1.33,1.33)
將(1.33,1.33)位置的像素賦值給(2,2),完成插值。
代碼實現
Java代碼開發
最近鄰插值算法java代碼_圖像最近鄰插值算法_異域拾荒人的博客-CSDN博客
https://blog.csdn.net/weixin_32024145/article/details/114813888
使用Android JNI開發
使用opencv 庫開發,因為需要獲取像素等操作,最核心的代碼為:??
????//?根據縮放比例計算輸出圖像的寬高 ????int?new_width?=?static_cast
于其只考慮最近鄰像素的值,而忽略了其他像素的信息,因此會導致圖像插值后的結果較為粗糙,缺乏細節和平滑性
直接使用離插值位置最近的整數位置的像素作為插值像素,這樣會導致相鄰兩個插值像素有很大的概率是相同的
應用場景
快速預覽圖像或圖像縮小等場景。 ?
雙線性插值算法
? 雙線性插值算法是一種常用的圖像插值算法,它能夠通過對周圍4個已知像素進行加權平均來計算待插值像素的像素值,從而獲得更為平滑和細膩的插值結果。聽著就比最近鄰插值算法復雜,但是效果肯定比它優。 ? 雙線性插值算法的具體實現過程如下: ? 確定待插值像素位置,假設其坐標為(x,y)。找到距離(x,y)最近的四個已知像素,假設它們的坐標為(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)。計算待插值像素的像素值。假設待插值像素的像素值為f(x,y),則可以通過下面的公式計算: ? ?
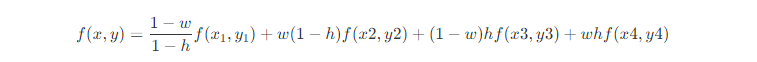
? 其中,w和h分別表示待插值像素相對于(x1,y1)和(x2,y2)的水平距離和垂直距離,具體計算方式如下: ?
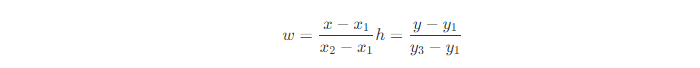
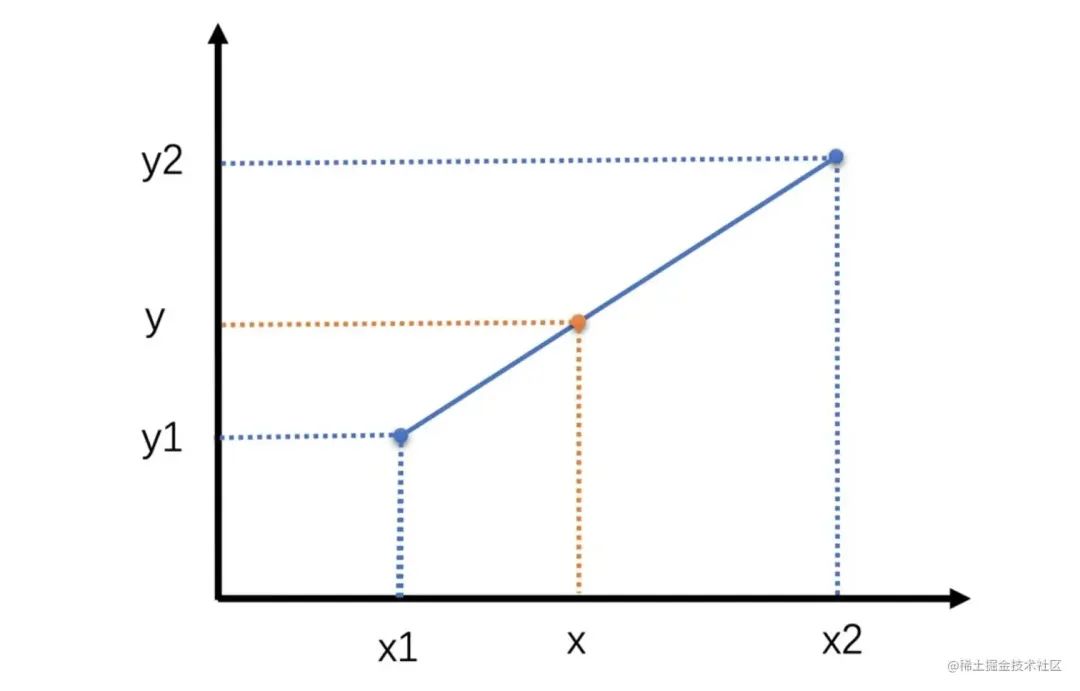
? 將計算得到的像素值賦給待插值像素。 ? 線性插值 ? 線性插值是一種數學方法,用于在兩個已知點之間估計未知點的值。它假定兩個已知點之間的函數是線性的,因此可以使用直線方程來計算未知點的值。 ? 線性插值認為,這個需要插值得到的點跟這兩個已知點都有一定的關系,并且,待插值點與離它近的那個點更相似。因此,線性插值是一種以距離作為權重的插值方式,距離越近權重越大,距離越遠權重越小。 ? 比如,如下圖所示,已知 (x1,y1)與(x2,y2)兩個點,需求得x對應的y值。 ?
?
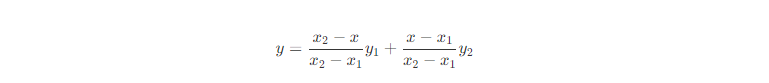
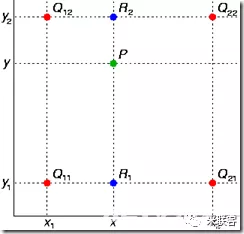
? 它表示在兩個點(x1,y1)和(x2,y2)之間,對于給定的x值,對應的y值可以通過這個公式計算得到。當x=x1時,y=y1;當 x=x2 時,y=y2。當x在x1和x2之間時,y 的值在y1和y2之間線性變化。 ? 雙線性插值 ? 雙線性插值本質上就是在兩個方向上做線性插值。由于圖像是兩個方向的二維數據,正好適合使用雙線性插值算法。雙線性插值其實就是三次線性插值的過程,我們先通過兩次線性插值得到兩個中間值,然后再通過對這兩個中間值進行一次插值得到最終的結果。 ? 假設我們有一個矩形網格,其中四個頂點的坐標分別為 (x1,y1),(x1,y2),(x2,y1) 和 (x2,y2),并且這些點的函數值分別為 f(x1,y1),f(x1,y2),f(x2,y1) 和 f(x2,y2)。我們想要計算點 (x,y) 的函數值,其中 x 和 y 分別在 x1 和 x2 之間,在 y1 和 y2 之間。 ?
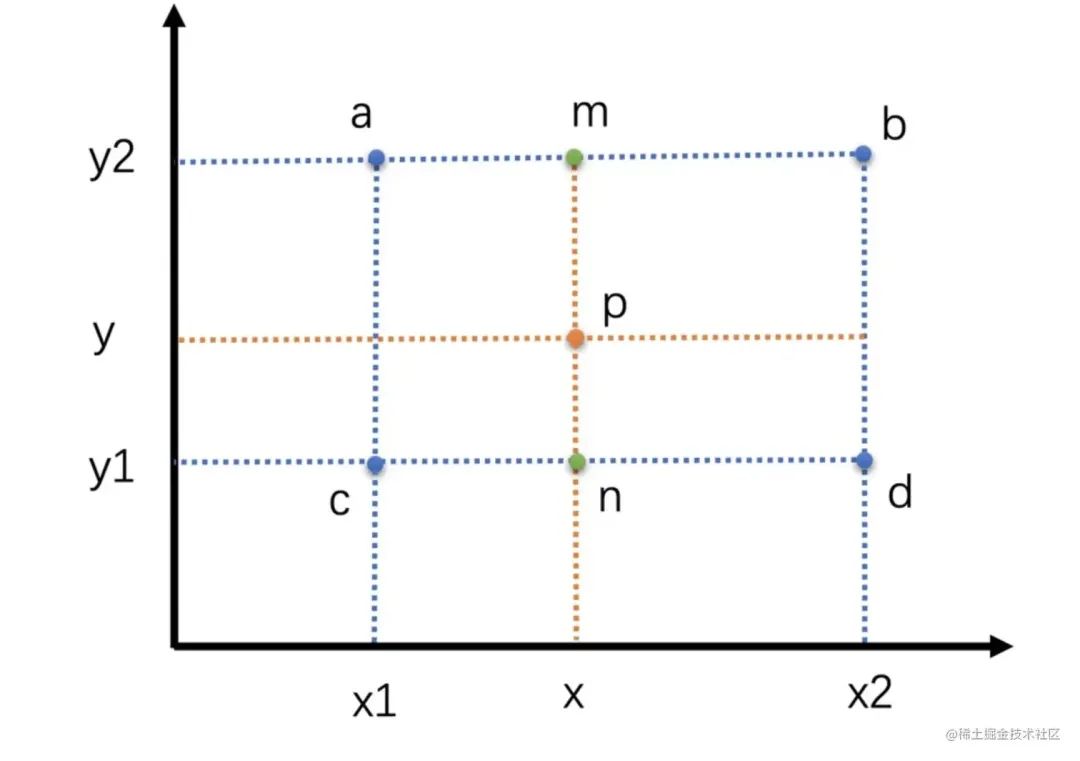
? 沿著x軸進行線性插值,得到兩個臨時值。 ?
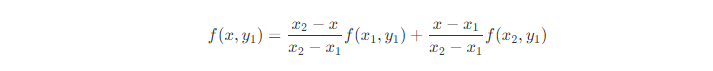
? 這個即圖中的n點。 ?
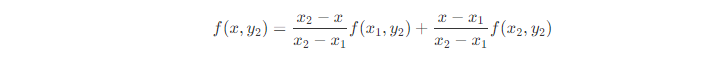
? 即圖的m點,再沿著y軸線性插值。 ?
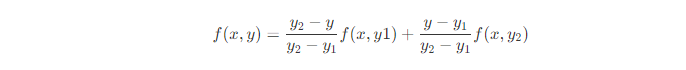
? ? 即圖中p以720P放大到1080P為例,那么1080P圖像中的目標像素點(2,2)的雙線性插值過程是怎么樣的呢? ? 首先,將目標像素點(2,2)映射到原圖像的(1.33,1.33)位置,對應下面圖中的點p。找到(1.33,1.33)周圍的4個像素(1,1)、(2,1)、(1,2)和(2,2),分別對應圖中的點a、b、c和d。 ?
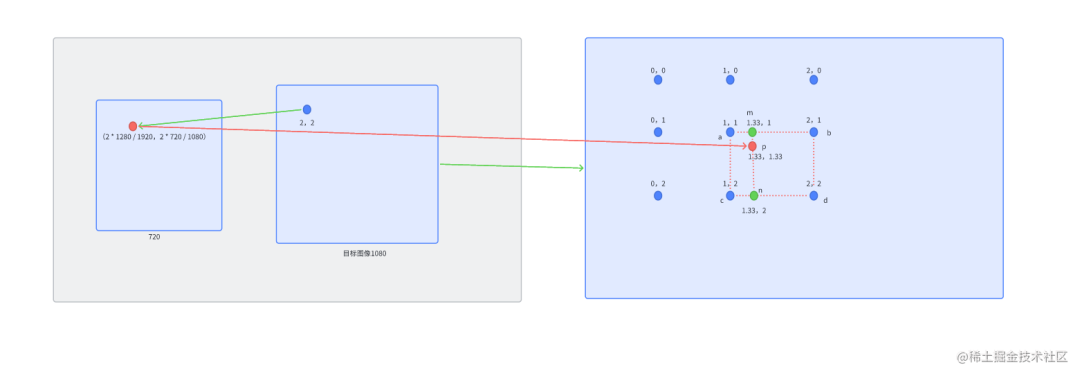
? 根據上述的公式,我們可以計算出圖中的n、m 最后求出p 的像素。 ? 首先n點: ?
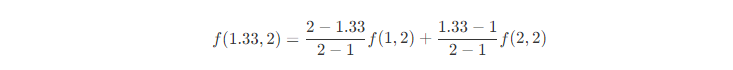
? m點: ?
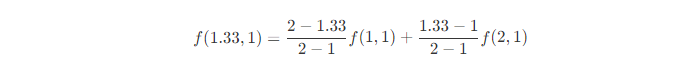
? p點: ?
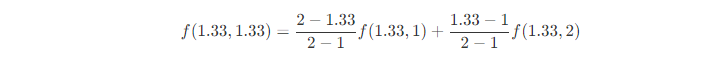
? 值求得(1.33,1.33)的值之后,將其賦值給1080P目標圖像的(2,2)位置的像素點就可以了。這就是雙線性插值的過程。 ? 優缺點 ? 優點:可以獲得相對較為平滑和細膩的插值結果,而且計算速度也比較快 缺點: ?
只考慮了周圍4個像素的信息,因此在圖像放大的情況下,仍然會出現鋸齒狀的效果
在圖像存在大幅度變化或復雜紋理的情況下,雙線性插值算法可能會導致圖像失真或出現馬賽克效果
應用場景 ? 圖像放大、縮小和旋轉等場景 ?
總結
此文章主在弄明白圖像縮放的原理,并完成了經典算法插值算法的最近鄰插值算法,當然,最近鄰插值算法的使用場景單一,也不是工作中常用的算法,后續會陸續完成雙三次插值算法。雙三次算法圖像質量方面有明顯提升,特別是在縮小圖像時,雙三次插值算法可以更好地保留圖像的細節和紋理。
? 編輯:黃飛
?
 電子發燒友App
電子發燒友App

























評論