PID 算法可以用于溫度控制、水位控制、飛行姿態控制等領域。

后面我們通過PID 控制電機進行說明。

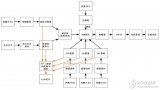
自動控制系統

在直流有刷電機的基礎驅動中，如果電機負載不變，我們只要設置固定的占空比（電壓），電機的速度就會穩定在目標范圍。

然而，在實際的應用中，負載可能會發生變化，此時如果還是輸出固定的電壓，電機的速度就偏離目標范圍了，為了解決這個問題，我們需要引入自動控制系統中的閉環控制。接下來我們開始學習自動控制系統的內容。

概念：用自動控制裝置，對關鍵參數進行自動控制，使它在受到外界干擾而偏離正常狀態時，能夠被自動地調節回到目標范圍內。

應用場景：電水壺保溫系統?、大棚溫控系統、水位控制系統，等等。

分類：自動控制系統分為開環控制系統和閉環控制系統?。

① 開環控制系統

在開環控制系統中，系統輸出只受輸入的控制，沒有反饋回路，控制精度和抑制干擾的特性都比較差。

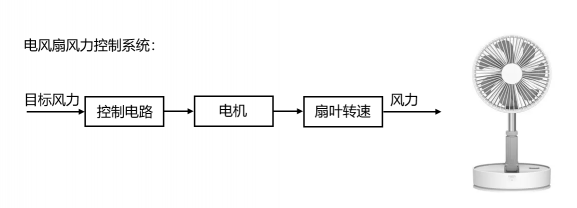
電風扇風力控制系統就是一個開環控制的系統，我們設置好目標風力之后，控制電路就輸出相應的電壓（假設是電壓控制），此時電機的扇葉轉速就被控制在目標范圍了。

理想狀態下，風扇的輸出風力確實可以穩定在目標值附近，然而，在實際的使用中，電機會逐漸老化，扇葉上的灰塵也會讓負載增大，此時我們所設定目標風力和實際風力可能就存在偏差了。

②閉環控制系統

在閉環控制系統中，引入了反饋回路，利用輸出（實際值）和輸入（目標值）的偏差，對系統進行控制，避免偏離預定目標。

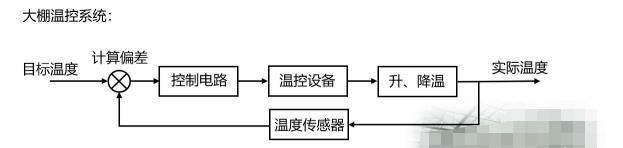
大棚溫控系統就是一個閉環控制的系統，我們設置好目標溫度之后，溫度傳感器會采集棚內的實際溫度，然后將目標溫度和實際溫度進行偏差的計算，計算后的結果輸入到控制電路中，控制電路進一步控制溫控設備進行升溫和降溫，此時棚內的實際溫度就被控制在目標范圍了。

當實際溫度因外部影響偏離目標值時，溫度傳感器（反饋電路）就能及時的反饋偏差，讓系統自動調節溫控設備，使得實際溫度逐漸回到目標范圍。

PID 算法

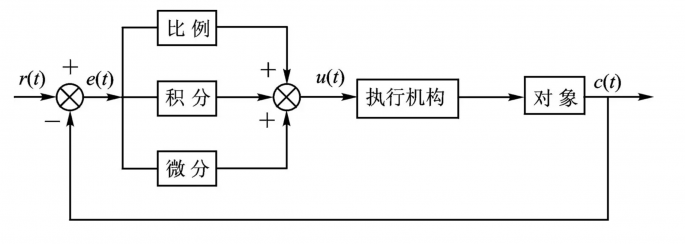
PID 算法是閉環控制系統中常用的算法，PID 分別是 Proportion（比例）、Integral（積分）、Differential（微分）的首字母縮寫。它是一種結合比例、積分和微分三個環節于一體的閉環控制算法。

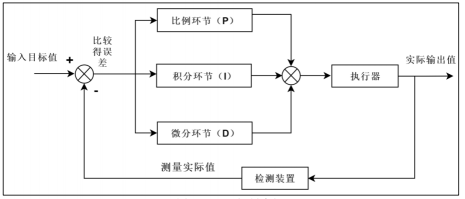
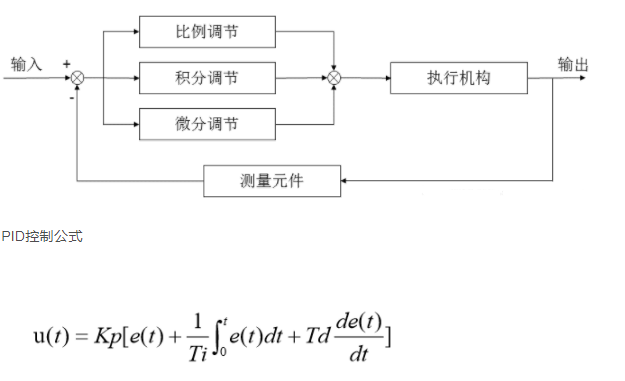
我們將輸入目標值和實際輸出值進行偏差的計算，然后把計算結果輸入到 PID控制算法中，經過比例、積分和微分三個環節的運算，運算后的輸出作用于執行器，從而讓系統的實際值逐漸靠近目標值。

以大棚溫控系統為例，來理解 PID 算法中三個環節的作用。

比例環節（ Proportion）

比例環節可以成比例地反應控制系統的偏差信號，即輸出與輸入偏差成正比，可以用來減小系統的偏差。公式如下：

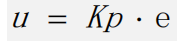
u —輸出

Kp—比例系數

e —偏差

我們可以通過大棚溫控去理解PID公式。例如需要調節棚內溫度為 30℃，而實際溫度為 10℃，此時的偏差 e=20，由比例環節的公式可知

當 e 確定時，Kp 越大則輸出u 越大，也就是溫控系統的調節力度越大，這樣就可以更快地達到目標溫度；而當 Kp 確定時，偏差 e 越大則輸出 u 越大。

由此可見，在比例環節中，比例系數 Kp 和偏差 e 越大則系統消除偏差的時間越短

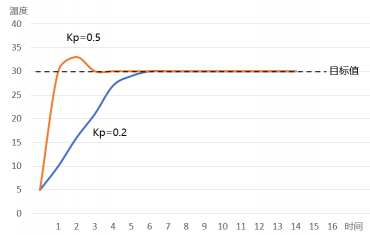
當 Kp 的值越大時，其對應的橙色曲線達到目標值的時間就越短，與此同時，橙色曲線出現了一定幅度的超調和振蕩，這會使得系統的穩定性下降。

所以我們在設置比例系數的時候，并不是越大越好，而是要兼顧消除偏差的時間以及整個系統的穩定性。

在實際的應用中，如果僅有比例環節的控制，可能會給系統帶來一個問題：靜態誤差。

靜態誤差是指系統控制過程趨于穩定時，目標值與實測值之間的偏差。

如果我們在需要調節棚內溫度為 30℃，而實際溫度為 25℃，此時偏差 e=5，Kp 為固定值，那么此時的輸出可以讓大棚在半個小時之內升溫 5℃，而外部的溫差可以讓大棚在半個小時之內降溫 5℃，也就是說，輸出 u 的作用剛好被外部影響抵消了，這就使得偏差會一直存在。

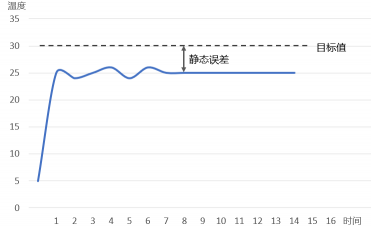
我們可以通過增大 Kp 來增大輸出，以此消除偏差。在實際應用中，此方法的局限性很大，因為我們不能確定偏差的大小，它是在實時變化的，如果我們把 Kp 設置得太大，就會引入超調和振蕩，讓整個系統的穩定性變差。因此，為了消除靜態誤差，我們引入了積分環節。

積分環節（Integral）

積分環節可以對偏差 e 進行積分，只要存在偏差，積分環節就會不斷起作用，主要用于消除靜態誤差，提高系統的無差度。

引入積分環節后，比例+積分環節的公式如下：

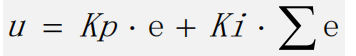
u —輸出

e —?偏差

∑e—累計偏差

Kp—?比例系數

Ki—積分系數

通過以大棚溫控分析可以知道，如果溫控系統的比例環節作用被抵消，存在靜態誤差 5℃，此時偏差存在，積分環節會一直累計偏差，以此增大輸出，從而消除靜態誤差。

從上述公式中可以得知，當積分系數 Ki 或者累計偏差越大時，輸出就越大，系統消除靜態誤差的時間就越短。

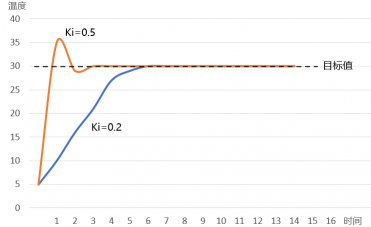
當?Ki?的值越大時，其對應的橙色曲線達到目標值的時間就越短，與此同時，橙色曲線出現了一定幅度的超調和振蕩，這會使得系統的穩定性下降

因此，我們在設置積分系數的時候，并不是越大越好，而是要兼顧消除靜態誤差的時間以及整個系統的穩定性。

只要系統還存在偏差，積分環節就會不斷地累計偏差。當系統偏差為 0的時候，說明已經達到目標值，此時的累計偏差不再變化，但是積分環節依舊在發揮作用（此時往往作用最大），這就很容易產生超調的現象了。

因此，我們需要引入微分環節，提前減弱輸出，抑制超調的發生。

微分環節（Differential）

微分環節可以反應偏差量的變化趨勢，根據偏差的變化量提前作出相應控制，減小超調，克服振蕩。引入微分環節后，比例+積分+微分環節的公式如下：

?

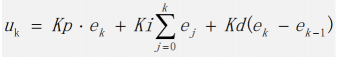
我們繼續使用大棚溫控去分析微分環節的作用。如果溫控系統目標溫度為 30℃，在上午八點的時候存在偏差15℃，經過一段時間的調節，到了上午九點，此時偏差已經縮小到5℃，偏差的變化量= 九點的偏差（第 k 次）-八點的偏差（第 k-1 次）= -10，結合上述公式可知，此時微分環節會削弱比例和積分環節的作用，減小輸出以抑制超調。

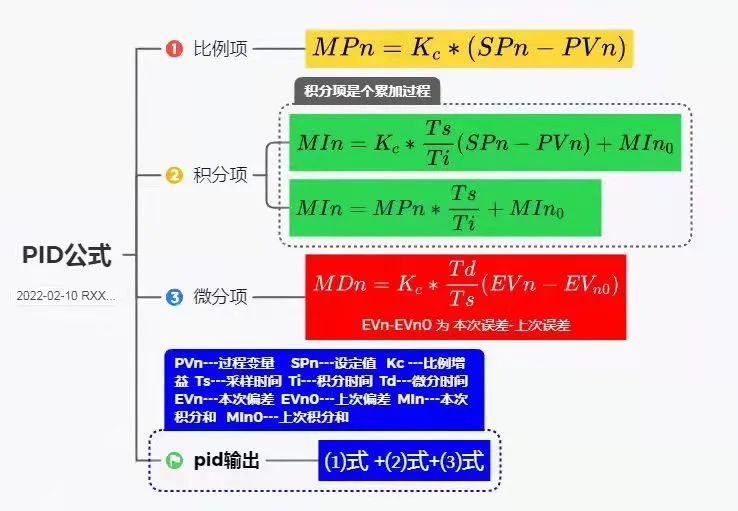
最終得到了一個 PID算法公式：

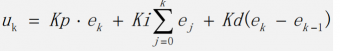
這個公式是 PID 離散公式之一，除了離散公式之外，PID 還有連續的公式，但是因為連續的公式不利于機器計算，我們一般不研究。每一個系統的 PID 系數并不是通用的，這需要根據實際的情況去設置。

PID 算法離散公式

位置式 PID 公式

?

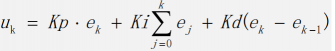
這個公式的計算需要全部控制量參與，它的每一次輸出都和過去的狀態有關。

增量式 PID 公式

通過位置式的 PID 公式，可推導出增量式 PID 公式

將 k = k-1 代入位置式 PID 公式

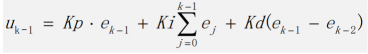
由

增量式 PID 可以看出，增量式 PID 的計算并不需要一直累計偏差，它的輸出與近三次的偏差有很大關系。

注意：增量式 PID 公式輸出的只是控制量的增量。假設電機實際轉速為 50RPM，現在我們要讓它加速到 60RPM，如果采用的是位置式 PID，系統將直接輸出 60RPM 對應的控制量（占空比）；

如果采用的是增量式 PID，系統將輸出提速 10RPM對應的控制量（占空比），此時我們還需要加上上次（50RPM）的輸出。

兩個 PID 公式的不同點

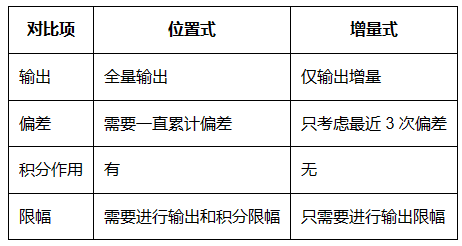
兩種?PID?公式的優缺點

① 位置式：

優點：位置式 PID 是一種非遞推式算法，帶有積分作用，適用于不帶積分部件的對象。

缺點：全量計算，計算錯誤影響很大；需要對偏差進行累加，運算量大。

② 增量式：

優點：只輸出增量，計算錯誤影響小；不需要累計偏差，運算量少，實時性相對較好。

缺點：積分截斷效應大，有穩態誤差。

積分飽和問題

在位置式 PID 中，如果系統長時間無法達到目標值，累計偏差（積分）就會變得很大，此時系統的響應就很慢了。

例如某個電機能達到的最大速度為 300RPM，而我們設置了目標速度為 350RPM，這明顯是一個不合理的目

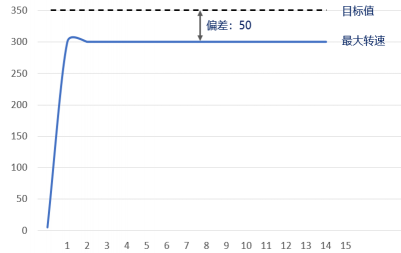
由于系統長時間無法達到目標值，累計偏差（積分）會變得越來越大，逐漸達到深度飽和的狀態，此時我們再設置一個合理范圍的目標速度（例如 200RPM），系統就沒有辦法在短時間內響應了。

為了避免位置式 PID 中可能出現的積分飽和問題，可以考慮下面解決方法：

①?優化 PID 曲線，系統越快達到目標值，累計的偏差就越小；

②?限制目標值調節范圍，規避可以預見的偏差；

③?進行積分限幅，在調整好 PID 系數之后，根據實際系統來選擇限幅范圍。

PID?算法代碼實現

控制量相關的結構體

我們知道PID 的離散化公式后，實現 PID 算法的代碼是非常簡單。

定義結構體來管理這些控制量

typedef struct
{
 __IO float SetPoint; /* 目標值 */
 __IO float ActualValue; /* 期望輸出值 */
 __IO float SumError; /* 偏差累計 */
 __IO float Proportion; /* 比例系數 P */
 __IO float Integral; /* 積分系數 I */
 __IO float Derivative; /* 微分系數 D */
 __IO float Error; /* Error[1],第 k 次偏差 */
 __IO float LastError; /* Error[-1],第 k-1 次偏差 */
 __IO float PrevError; /* Error[-2],第 k-2 次偏差 */
} PID_TypeDef;

PID 算法代碼

位置式 PID 代碼

/*
* @brief pid 閉環控制
* @param *PID：PID 結構體變量地址
* @param Feedback_value：當前實際值
* @retval 期望輸出值
*/
int32_t own_pid_ctrl(PID_TypeDef *PID,float Feedback_value)
{
 ? ?PID->Error = (float)(PID->SetPoint - Feedback_value); /* 計算偏差 */
 ? ?PID->SumError += PID->Error; /* 累計偏差 */
 ? ?PID->ActualValue = (PID->Proportion * PID->Error) /* 比例環節 */
 ? ?+ (PID->Integral * PID->SumError) /* 積分環節 */
 ? ?+ (PID->Derivative * (PID->Error - PID->LastError)); /* 微分環節 */
 ? ?PID->LastError = PID->Error; /* 存儲偏差，用于下次計算 */
 ? ?return ((int32_t)(PID->ActualValue)); /* 返回計算后輸出的數值 */
}

own_pid_ctrl 函數用來進行位置式 PID 的控制，該函數的 2 個形參：PID 傳入 PID控制量相關的結構體地址；Feedback_value 傳入當前系統的實際值，用于計算偏差。

在函數中，我們先計算本次偏差 Error，然后把偏差累計，存入 SumError 成員當中，接著根據位置式的公式進行三個環節的計算，計算后的期望輸出存入 ActualValue 成員當中，然后存儲本次偏差，最后返回期望輸出值。

增量式 PID 代碼

/*
* @brief pid 閉環控制
* @param *PID：PID 結構體變量地址
* @param Feedback_value：當前實際值
* @retval 期望輸出值
*/
int32_t own_pid_ctrl(PID_TypeDef *PID,float Feedback_value)
{
    PID->Error = (float)(PID->SetPoint - Feedback_value); /* 計算偏差 */
    PID->ActualValue += 
    /* 比例環節 */
    (PID->Proportion * (PID->Error - PID->LastError)) 
    /* 積分環節 */ 
    + (PID->Integral * PID->Error) 
    /* 微分環節 */
    + (PID->Derivative * (PID->Error - 2 * PID->LastError + PID->PrevError)); 
    PID->PrevError = PID->LastError; /* 存儲偏差，用于下次計算 */
    PID->LastError = PID->Error;
    return ((int32_t)(PID->ActualValue)); /* 返回計算后輸出的數值 */
}

增量式 PID 的代碼實現和位置式是非常類似的，所以我們在實際的代碼實現中，可以通過一個宏定義來切換這兩種不同的算法，值得注意的是，增量式 PID 輸出的是調節量，所以計算期望輸出值 ActualValue 的時候是自增運算，這一點和位置式 PID 是不一樣的。

編輯：黃飛