des算法原理
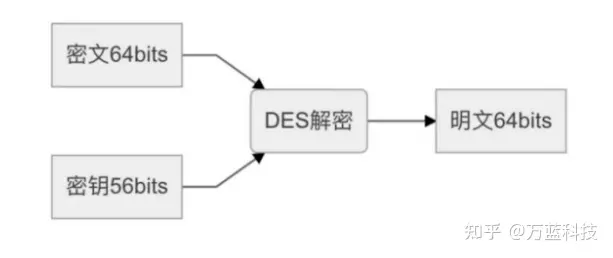
DES算法全稱為Data Encryption Standard,即數(shù)據(jù)加密算法,它是IBM公司于1975年研究成功并公開發(fā)表的。DES算法的入口參數(shù)有三個:Key、Data、Mode。其中Key為8個字節(jié)共64位,是DES算法的工作密鑰;Data也為8個字節(jié)64位,是要被加密或被解密的數(shù)據(jù);Mode為DES的工作方式,有兩種:加密或解密。
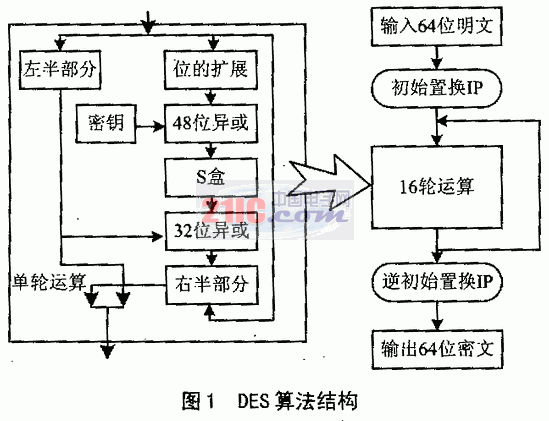
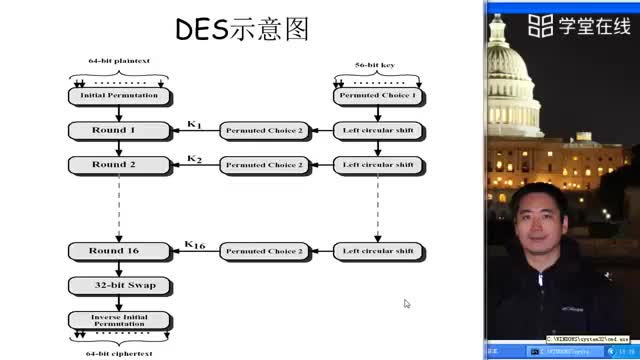
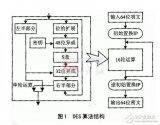
DES算法把64位的明文輸入塊變?yōu)?4位的密文輸出塊,它所使用的密鑰也是64位,其算法主要分為兩步:
1?初始置換
其功能是把輸入的64位數(shù)據(jù)塊按位重新組合,并把輸出分為L0、R0兩部分,每部分各長3 2位,其置換規(guī)則為將輸入的第58位換到第一位,第50位換到第2位……依此類推,最后一位是原來的第7位。L0、R0則是換位輸出后的兩部分,L0是輸出的左32位,R0是右32位,例:設(shè)置換前的輸入值為D1D2D3……D64,則經(jīng)過初始置換后的結(jié)果為:L0=D58D50……D8;R0=D57D49……D7。
2?逆置換
經(jīng)過16次迭代運算后,得到L16、R16,將此作為輸入,進行逆置換,逆置換正好是初始置換的逆運算,由此即得到密文輸出。
RSA算法簡介
這種算法1978年就出現(xiàn)了,它是第一個既能用于數(shù)據(jù)加密也能用于數(shù)字簽名的算法。它易于理解和操作,也很流行。算法的名字以發(fā)明者的名字命名:Ron Rivest, AdiShamir 和Leonard Adleman。但RSA的安全性一直未能得到理論上的證明。
RSA的安全性依賴于大數(shù)分解。公鑰和私鑰都是兩個大素數(shù)( 大于 100個十進制位)的函數(shù)。據(jù)猜測,從一個密鑰和密文推斷出明文的難度等同于分解兩個大素數(shù)的積。
密鑰對的產(chǎn)生。選擇兩個大素數(shù),p 和q 。計算:
n = p * q
然后隨機選擇加密密鑰e,要求 e 和 ( p - 1 ) * ( q - 1 ) 互質(zhì)。最后,利用Euclid 算法計算解密密鑰d, 滿足
e * d = 1 ( mod ( p - 1 ) * ( q - 1 ) )
其中n和d也要互質(zhì)。數(shù)e和n是公鑰,d是私鑰。兩個素數(shù)p和q不再需要,應(yīng)該丟棄,不要讓任何人知道。
加密信息 m(二進制表示)時,首先把m分成等長數(shù)據(jù)塊 m1 ,m2,..., mi ,塊長s,其中 2^s <= n, s 盡可能的大。對應(yīng)的密文是:
ci = mi^e ( mod n ) ( a )
解密時作如下計算:
mi = ci^d ( mod n ) ( b )
RSA 可用于數(shù)字簽名,方案是用 ( a ) 式簽名, ( b )式驗證。具體操作時考慮到安全性和 m信息量較大等因素,一般是先作 HASH 運算。
RSA 的安全性。
RSA的安全性依賴于大數(shù)分解,但是否等同于大數(shù)分解一直未能得到理論上的證明,因為沒有證明破解RSA就一定需要作大數(shù)分解。假設(shè)存在一種無須分解大數(shù)的算法,那它肯定可以修改成為大數(shù)分解算法。目前, RSA的一些變種算法已被證明等價于大數(shù)分解。不管怎樣,分解n是最顯然的攻擊方法。現(xiàn)在,人們已能分解140多個十進制位的大素數(shù)。因此,模數(shù)n必須選大一些,因具體適用情況而定。
RSA的速度。
由于進行的都是大數(shù)計算,使得RSA最快的情況也比DES慢上100倍,無論是軟件還是硬件實現(xiàn)。速度一直是RSA的缺陷。一般來說只用于少量數(shù)據(jù)加密。
RSA的選擇密文攻擊。
RSA在選擇密文攻擊面前很脆弱。一般攻擊者是將某一信息作一下偽裝(Blind),讓擁有私鑰的實體簽署。然后,經(jīng)過計算就可得到它所想要的信息。實際上,攻擊利用的都是同一個弱點,即存在這樣一個事實:乘冪保留了輸入的乘法結(jié)構(gòu):
( XM )^d = X^d *M^d mod n
前面已經(jīng)提到,這個固有的問題來自于公鑰密碼系統(tǒng)的最有用的特征--每個人都能使用公鑰。但從算法上無法解決這一問題,主要措施有兩條:一條是采用好的公鑰協(xié)議,保證工作過程中實體不對其他實體任意產(chǎn)生的信息解密,不對自己一無所知的信息簽名;另一條是決不對陌生人送來的隨機文檔簽名,簽名時首先使用One-Way Hash Function對文檔作HASH處理,或同時使用不同的簽名算法。在中提到了幾種不同類型的攻擊方法。
RSA的公共模數(shù)攻擊。
若系統(tǒng)中共有一個模數(shù),只是不同的人擁有不同的e和d,系統(tǒng)將是危險的。最普遍的情況是同一信息用不同的公鑰加密,這些公鑰共模而且互質(zhì),那末該信息無需私鑰就可得到恢復(fù)。設(shè)P為信息明文,兩個加密密鑰為e1和e2,公共模數(shù)是n,則:
C1 = P^e1 mod n
C2 = P^e2 mod n
密碼分析者知道n、e1、e2、C1和C2,就能得到P。
因為e1和e2互質(zhì),故用Euclidean算法能找到r和s,滿足:
r * e1 + s * e2 = 1
假設(shè)r為負(fù)數(shù),需再用Euclidean算法計算C1^(-1),則
( C1^(-1) )^(-r) * C2^s = P mod n
另外,還有其它幾種利用公共模數(shù)攻擊的方法。總之,如果知道給定模數(shù)的一對e和d,一是有利于攻擊者分解模數(shù),一是有利于攻擊者計算出其它成對的e’和d’,而無需分解模數(shù)。解決辦法只有一個,那就是不要共享模數(shù)n。
RSA的小指數(shù)攻擊。 有一種提高RSA速度的建議是使公鑰e取較小的值,這樣會使加密變得易于實現(xiàn),速度有所提高。但這樣作是不安全的,對付辦法就是e和d都取較大的值。
RSA算法是第一個能同時用于加密和數(shù)字簽名的算法,也易于理解和操作。 RSA是被研究得最廣泛的公鑰算法,從提出到現(xiàn)在已近二十年,經(jīng)歷了各種攻擊的考驗,逐漸為人們接受,普遍認(rèn)為是目前最優(yōu)秀的公鑰方案之一。RSA的安全性依賴于大數(shù)的因子分解,但并沒有從理論上證明破譯RSA的難度與大數(shù)分解難度等價。即RSA的重大缺陷是無法從理論上把握它的保密性能如何,而且密碼學(xué)界多數(shù)人士傾向于因子分解不是NPC問題。RSA的缺點主要有:A)產(chǎn)生密鑰很麻煩,受到素數(shù)產(chǎn)生技術(shù)的限制,因而難以做到一次一密。B)分組長度太大,為保證安全性,n 至少也要 600 bits以上,使運算代價很高,尤其是速度較慢,較對稱密碼算法慢幾個數(shù)量級;且隨著大數(shù)分解技術(shù)的發(fā)展,這個長度還在增加,不利于數(shù)據(jù)格式的標(biāo)準(zhǔn)化。目前,SET(Secure Electronic Transaction)協(xié)議中要求CA采用2048比特長的密鑰,其他實體使用1024比特的密鑰
DES算法原理:
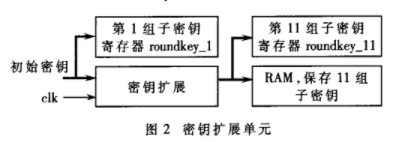
處理密鑰:
從用戶處獲得64位密鑰.(每第8位為校驗位,為使密鑰有正確的奇偶校驗,每個密鑰要有奇數(shù)個"1"位.(本文如未特指,均指二進制位)
具體過程:
對密鑰實施變換,使得變換以后的密鑰的各個位與原密鑰位對應(yīng)關(guān)系如下表所示:(表一為忽略校驗位以后情況).
57 49 41 33 25 17 9 1 58 50 42 34 26 18
10 2 59 51 43 35 27 19 11 3 60 52 44 36
63 55 47 39 31 23 15 7 62 54 49 38 30 22
14 6 61 53 45 37 29 21 13 5 28 20 12 4
把變換后的密鑰等分成兩部分,前28位記為C[0],后28位記為D[0].
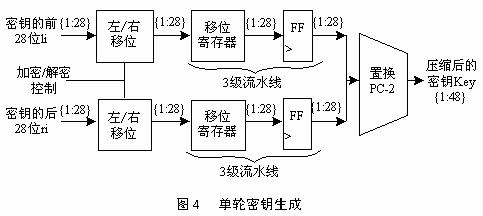
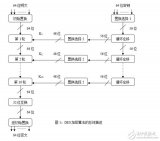
計算子密鑰(共16個), 從i=1開始。
分別對C[i-1],D[i-1]作循環(huán)左移來生成C[i],D[i].(共16次)。
每次循環(huán)左移位數(shù)如下表所示:
輪 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
位數(shù) 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
串聯(lián)C[i],D[i],得到一個56位數(shù),然后對此數(shù)
作如下變換以產(chǎn)生48位子密鑰K[i]。
變換過程如下:
14 17 11 24 1 5 3 28 15 6 21 10
23 19 12 4 26 8 16 7 27 20 13 2
41 52 31 37 47 55 30 40 51 45 33 48
44 49 39 56 34 53 46 42 50 36 29 32
1.2.3.3 按以上方法計算出16個子密鑰。
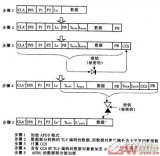
對64位數(shù)據(jù)塊的處理:
把數(shù)據(jù)分成64位的數(shù)據(jù)塊,不夠64位的以適當(dāng)?shù)姆绞教钛a。
對數(shù)據(jù)塊作變換。
58 50 42 34 26 18 10 2 60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6 64 56 48 40 32 24 16 8
57 49 41 33 25 17 9 1 59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5 63 55 47 39 31 23 15 7
將變換后的數(shù)據(jù)塊等分成前后兩部分,前32位記為L[0],后32位記為R[0]。
用16個子密鑰對數(shù)據(jù)加密。
根據(jù)下面的擴沖函數(shù)E,擴展32位的成48位
32 1 2 3 4 5 4 5 6 7 8 9
8 9 10 11 12 13 12 13 14 15 16 17
16 17 18 19 20 21 20 21 22 23 24 25
24 25 26 27 28 29 28 29 30 31 32 1
用E{R[i-1]}與K[i]作異或運算。
把所得的48位數(shù)分成8個6位數(shù)。1-6位為B[1],7-12位為B[2],... 43-48位為B[8]。
用S密箱里的值替換B[j]。從j=1開始。S密箱里的值為4位數(shù),共8個S密箱.
取出B[j]的第1和第6位串聯(lián)起來成一個2位數(shù),記為m.m即是S密箱里用來替換B[j]的數(shù)所在的列數(shù)。
取出B[j]的第2至第5位串聯(lián)起來成一個4位數(shù),記為n。n即是S密箱里用來替換B[j]的數(shù)所在的行數(shù)。
用S密箱里的值S[j][ m][ n]替換B[j]。8個S密箱如下所示:
S-BOXE:S1
Binary d1d6 =>; 00 01 10 11
\/ d2..d5 \/ Dec 0 1 2 3
0000 0 14 0 4 15
0001 1 4 15 1 12
0010 2 13 7 14 8
0011 3 1 4 8 2
0100 4 2 14 13 4
0101 5 15 2 6 9
0110 6 11 13 2 1
0111 7 8 1 11 7
1000 8 3 10 15 5
1001 9 10 6 12 11
1010 10 6 12 9 3
1011 11 12 11 7 14
1100 12 5 9 3 10
1101 13 9 5 10 0
1110 14 0 3 5 6
1111 15 7 8 0 13
S-BOXE:S2
Binary d1d6 =>; 00 01 10 11
\/ d2..d5 \/ Dec 0 1 2 3
0000 0 15 3 0 13
0001 1 1 13 14 8
0010 2 8 4 7 10
0011 3 14 7 11 1
0100 4 6 15 10 3
0101 5 11 2 4 15
0110 6 3 8 13 4
0111 7 4 14 1 2
1000 8 9 12 5 11
1001 9 7 0 8 6
1010 10 2 1 12 7
1011 11 13 10 6 12
1100 12 12 6 9 0
1101 13 0 9 3 5
1110 14 5 11 2 14
1111 15 10 5 15 9
S-BOXE:S3
Binary d1d6 =>; 00 01 10 11
\/ d2..d5 \/ Dec 0 1 2 3
0000 0 10 13 13 1
0001 1 0 7 6 10
0010 2 9 0 4 13
0011 3 14 9 9 0
0100 4 6 3 8 6
0101 5 3 4 15 9
0110 6 15 6 3 8
0111 7 5 10 0 7
1000 8 1 2 11 4
1001 9 13 8 1 15
1010 10 12 5 2 14
1011 11 7 14 12 3
1100 12 11 12 5 11
1101 13 4 11 10 5
1110 14 2 15 14 2
1111 15 8 1 7 12
S-BOXE:S4
Binary d1d6 =>; 00 01 10 11
\/ d2..d5 \/ Dec 0 1 2 3
0000 0 7 13 10 3
0001 1 13 8 6 15
0010 2 14 11 9 0
0011 3 3 5 0 6
0100 4 0 6 12 10
0101 5 6 15 11 1
0110 6 9 0 7 13
0111 7 10 3 13 8
1000 8 1 4 15 9
1001 9 2 7 1 4
1010 10 8 2 3 5
1011 11 5 12 14 11
1100 12 11 1 5 12
1101 13 12 10 2 7
1110 14 4 14 8 2
1111 15 15 9 4 14
S-BOXE:S5
Binary d1d6 =>; 00 01 10 11
\/ d2..d5 \/ Dec 0 1 2 3
0000 0 2 14 4 11
0001 1 12 11 2 8
0010 2 4 2 1 12
0011 3 1 12 11 7
0100 4 7 4 10 1
0101 5 10 7 13 14
0110 6 11 13 7 2
0111 7 6 1 8 13
1000 8 8 5 15 6
1001 9 5 0 9 15
1010 10 3 15 12 0
1011 11 15 10 5 9
1100 12 13 3 6 10
1101 13 0 9 3 4
1110 14 14 8 0 5
1111 15 9 6 14 3
S-BOXE:S6
Binary d1d6 =>; 00 01 10 11
\/ d2..d5 \/ Dec 0 1 2 3
0000 0 12 10 9 4
0001 1 1 15 14 3
0010 2 10 4 15 2
0011 3 15 2 5 12
0100 4 9 7 2 9
0101 5 2 12 8 5
0110 6 6 9 12 15
0111 7 8 5 3 10
1000 8 0 6 7 11
1001 9 13 1 0 14
1010 10 3 13 4 1
1011 11 4 14 10 7
1100 12 14 0 1 6
1101 13 7 11 13 0
1110 14 5 3 11 8
1111 15 11 8 6 13
S-BOXE:S7
Binary d1d6 =>; 00 01 10 11
\/ d2..d5 \/ Dec 0 1 2 3
0000 0 4 13 1 6
0001 1 11 0 4 11
0010 2 2 11 11 13
0011 3 14 7 13 8
0100 4 15 4 12 1
0101 5 0 9 3 4
0110 6 8 1 7 10
0111 7 13 10 14 7
1000 8 3 14 10 9
1001 9 12 3 15 5
1010 10 9 5 6 0
1011 11 7 12 8 15
1100 12 5 2 0 14
1101 13 10 15 5 2
1110 14 6 8 9 3
1111 15 1 6 2 12
S-BOXE:S8
Binary d1d6 =>; 00 01 10 11
\/ d2..d5 \/ Dec 0 1 2 3
0000 0 13 1 7 2
0001 1 2 15 11 1
0010 2 8 13 4 14
0011 3 4 8 1 7
0100 4 6 10 9 4
0101 5 15 3 12 10
0110 6 11 7 14 8
0111 7 1 4 2 13
1000 8 10 12 0 15
1001 9 9 5 6 12
1010 10 3 6 10 9
1011 11 14 11 13 0
1100 12 5 0 15 3
1101 13 0 14 3 5
1110 14 12 9 5 6
1111 15 7 2 8 11
返回第一步直至8個數(shù)據(jù)塊都被替換。
把B[1]至B[8]順序串聯(lián)起來得到一個32位數(shù)。對這個數(shù)做如下變換:
bit goes to bit bit goes to bit
16 1 2 17
7 2 8 18
20 3 24 19
21 4 14 20
29 5 32 21
12 6 27 22
28 7 3 23
17 8 9 24
1 9 19 25
15 10 13 26
23 11 30 27
26 12 6 28
5 13 22 29
18 14 11 30
31 15 4 31
10 16 25 32
把得到的結(jié)果與L[i-1]作異或運算。把計算結(jié)果賦給R[i]。
把R[i-1]的值賦給L[i]。
從a循環(huán)執(zhí)行,直到K[16]也被用到。
把R[16]和L[16] 順序串聯(lián)起來得到一個64位數(shù)。對這個數(shù)實施II變換的逆變換。
以上就是DES算法如何加密一段64位數(shù)據(jù)塊。解密時用同樣的過程,只需把16個子密鑰的順續(xù)顛倒過來,應(yīng)用的順序為K[16],K[15],K[14],...K[1]。
 電子發(fā)燒友App
電子發(fā)燒友App






















評論