2、反向投影直方圖檢測(cè)ROI

　　圖像直方圖是什么？其實(shí)就是與圖像某一特征有關(guān)的數(shù)據(jù)集合的統(tǒng)計(jì)關(guān)系，反應(yīng)在歸一化直方圖中則是與該圖像特征有關(guān)的數(shù)據(jù)集合的概率關(guān)系。圖像某一子區(qū)域的直方圖可以看做是一個(gè)概率函數(shù)，它給出的是某個(gè)像素屬于該區(qū)域紋理特征的概率。還是上例子吧。

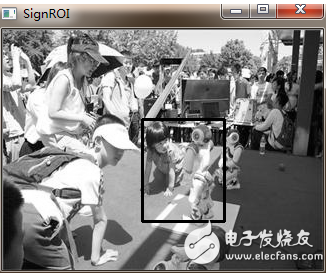
　　1） 求出上面灰度圖中矩形框標(biāo)記出的區(qū)域的歸一化灰度直方圖，為方便理解直方圖的每個(gè)bin只有一個(gè)像素，則每個(gè)bin的數(shù)值不就是這一像素值在圖片中出現(xiàn)的概率么。

　　2） 遍歷上面圖像中的每個(gè)像素，獲取其灰度值在直方圖（矩形框標(biāo)記區(qū)域）的bin的數(shù)值，用該數(shù)概率值代替原來(lái)像素的灰度值。

　　3） 得到的概率映射圖的每一像素不就代表了它屬于標(biāo)記區(qū)域的概率么？

　　從上例我們可以抽象出，方向投影直方圖的作用是在于替換一個(gè)輸入圖像中每個(gè)像素值，使其變成歸一化直方圖中對(duì)應(yīng)的概率值。OpenCV提供了反向投影直方圖操作的API函數(shù)calcBackProject，其函數(shù)原型為：

　　void calcBackProject（const Mat* arrays， //原始圖像

　　int narrays， //原始圖像張數(shù)

　　const int* channels， //原始圖像通道數(shù)量

　　const SparseMat& hist， //進(jìn)行反投影的直方圖

　　OutputArray backProject，//生成的反向投影圖像

　　const float** ranges， //直方圖每個(gè)維度的值域

　　double scale=1， //縮放因子

　　bool uniform=true ） //是否均勻12345678

　　很多參數(shù)與calcHist的意義類似，縮放因子表示對(duì)得到的反向投影圖像的每個(gè)“像素”可乘以一浮點(diǎn)數(shù)進(jìn)行縮放。

　　程序如下：

　　//CalcHistogram.h

　　#pragma once

　　#include “opencv2/core/core.hpp”

　　#include “opencv2/imgproc/imgproc.hpp”

　　#include “opencv2/highgui/highgui.hpp”

　　using namespace cv;

　　class CalcHistogram

　　{

　　private：

　　int histSize［3］; //直方圖項(xiàng)的數(shù)量

　　float hranges［2］; //h通道像素的最小和最大值

　　float sranges［2］;

　　float vranges［2］;

　　const float *ranges［3］; //各通道的范圍

　　int channels［3］; //三個(gè)通道

　　int dims;

　　Mat histogram; //用來(lái)存放 待反投影 的歸一化直方圖

　　public：

　　CalcHistogram（int hbins=90， int sbins=128， int vbins=128）;

　　~CalcHistogram（void）;

　　//計(jì)算直方圖

　　Mat getHistogram（const Mat &image）;

　　//畫(huà)出直方圖

　　void getHistogramImage（const Mat &image）;

　　//直方圖歸一化

　　void setHistogram（const Mat& h）;

　　//反投影直方圖檢測(cè)ROI

　　Mat reverseHistogram（const Mat& image）;

　　};

　　12345678910111213141516171819202122232425262728293031323334353637

　　CalcHistogram.cpp

　　//CalcHistogram.cpp

　　#include “CalcHistogram.h”

　　CalcHistogram：：CalcHistogram（int hbins， int sbins， int vbins）

　　{

　　histSize［0］=hbins;

　　histSize［1］=sbins;

　　histSize［2］=vbins;

　　hranges［0］=0; hranges［1］=180;

　　sranges［0］=0; sranges［1］=256;

　　vranges［0］=0; vranges［1］=256;

　　ranges［0］=hranges;

　　ranges［1］=sranges;

　　ranges［2］=vranges;

　　channels［0］=0;

　　channels［1］=1;

　　channels［2］=2;

　　dims=3;

　　}

　　CalcHistogram：：~CalcHistogram（void）

　　{

　　}

　　Mat CalcHistogram：：getHistogram（const Mat &image）

　　{

　　Mat hist;

　　calcHist（&image，

　　1，

　　channels，

　　Mat（），

　　hist，

　　dims，

　　histSize，

　　ranges，

　　true， //直方圖是均勻的

　　false

　　）;

　　return hist;

　　}

　　void CalcHistogram：：getHistogramImage（const Mat &image）

　　{

　　Mat hist=getHistogram（image）;

　　int scale = 4;

　　int hbins=histSize［0］;

　　int sbins=histSize［1］;

　　int vbins=histSize［2］;

　　float *hist_sta = new float［sbins］;

　　float *hist_val = new float［vbins］;

　　float *hist_hue = new float［hbins］;

　　memset（hist_val， 0， vbins*sizeof（float））;

　　memset（hist_sta， 0， sbins*sizeof（float））;

　　memset（hist_hue， 0， hbins*sizeof（float））;

　　for（ int s = 0; s 《 sbins; s++ ）

　　{

　　for（ int v = 0; v 《 vbins; v++ ）

　　{

　　for（int h=0; h《hbins; h++）

　　{

　　float binVal = hist.at《float》（h， s， v）;

　　hist_hue［h］ += binVal;

　　hist_val［v］ += binVal;

　　hist_sta［s］ += binVal;

　　}

　　}

　　}

　　double max_sta=0， max_val=0，max_hue=0;

　　for（int i=0; i《sbins; ++i）

　　{

　　if（hist_sta［i］》max_sta）

　　max_sta = hist_sta［i］;

　　}

　　for（int i=0; i《vbins; ++i）

　　{

　　if（hist_val［i］》max_val）

　　max_val = hist_val［i］;

　　}

　　for（int i=0; i《hbins; ++i）

　　{

　　if（hist_hue［i］》max_hue）

　　max_hue = hist_hue［i］;

　　}

　　Mat sta_img = Mat：：zeros（240， sbins*scale+20， CV_8UC3）;

　　Mat val_img = Mat：：zeros（240， vbins*scale+20， CV_8UC3）;

　　Mat hue_img = Mat：：zeros（240， hbins*scale+20， CV_8UC3）;

　　for（int i=0; i《sbins; ++i）

　　{

　　int intensity = cvRound（hist_sta［i］*（sta_img.rows-10）/max_sta）;

　　rectangle（sta_img， Point（i*scale+10， sta_img.rows-intensity），Point（（i+1）*scale-1+10， sta_img.rows-1）， Scalar（0，255，0）， 1）;

　　}

　　for（int i=0; i《vbins; ++i）

　　{

　　int intensity = cvRound（hist_val［i］*（val_img.rows-10）/max_val）;

　　rectangle（val_img， Point（i*scale+10， val_img.rows-intensity），Point（（i+1）*scale-1+10， val_img.rows-1）， Scalar（0，0，255）， 1）;

　　}

　　for（int i=0; i《hbins; ++i）

　　{

　　int intensity = cvRound（hist_hue［i］*（hue_img.rows-10）/max_hue）;

　　rectangle（hue_img， Point（i*scale+10， hue_img.rows-intensity），Point（（i+1）*scale-1+10， hue_img.rows-1）， Scalar（255，0，0）， 1）;

　　}

　　imshow（“Shist”， sta_img）;

　　imshow（“Vhist”， val_img）;

　　imshow（“Hhist”， hue_img）;

　　delete［］ hist_sta;

　　delete［］ hist_val;

　　delete［］ hist_hue;

　　}

　　void CalcHistogram：：setHistogram（const Mat& h）

　　{

　　histogram = h;

　　normalize（histogram，histogram， 1.0）;

　　}

　　Mat CalcHistogram：：reverseHistogram（const Mat& image）

　　{

　　Mat mapImg; //反向投影直方圖之后得到的概率圖

　　calcBackProject（&image，

　　1，

　　channels，

　　histogram，

　　mapImg，

　　ranges，

　　255.0

　　）;

　　return mapImg;

　　}

　　//main.cpp

　　#include 《iostream》

　　#include “CalcHistogram.h”

　　using namespace std;

　　bool draw;

　　Mat src;//原始圖像

　　Mat hsv;//原圖轉(zhuǎn)化為hsv

　　Mat roi;//ROI圖像

　　Point cursor;//初始坐標(biāo)

　　Rect rect;//標(biāo)記ROI的矩形框

　　void onMouse（int event， int x， int y， int flags， void *param）

　　{

　　Mat img = hsv.clone（）;

　　switch （event）

　　{

　　//按下鼠標(biāo)左鍵

　　case CV_EVENT_LBUTTONDOWN：

　　//點(diǎn)擊鼠標(biāo)圖像時(shí)，清除之前ROI圖像的顯示窗口

　　cvDestroyWindow（“ROI”）;

　　//存放起始坐標(biāo)

　　cursor = Point（x， y）;

　　//初始化起始矩形框

　　rect = Rect（x， y， 0， 0）;

　　draw = true;

　　break;

　　//松開(kāi)鼠標(biāo)左鍵

　　case CV_EVENT_LBUTTONUP：

　　if （rect.height 》 0 && rect.width 》 0）

　　{

　　//將img中的矩形區(qū)域復(fù)制給roi，并顯示在SignROI窗口

　　roi = img（Rect（rect.x， rect.y， rect.width， rect.height））;

　　rectangle（img， rect， Scalar（0， 0， 255），2）;

　　namedWindow（“SignROI”）;

　　imshow（“SignROI”， img）;

　　//將畫(huà)過(guò)矩形框的圖像用原圖像還原

　　hsv.copyTo（img）;

　　imshow（“SrcImage”， img）;

　　//顯示ROI圖像

　　namedWindow（“ROI”）;

　　imshow（“ROI”， roi）;

　　//計(jì)算ROI的直方圖并歸一化

　　CalcHistogram h;

　　Mat hist=h.getHistogram（roi）;

　　h.setHistogram（hist）;

　　//在hsv圖像上反向投影ROI的歸一化直方圖

　　Mat mapImage=h.reverseHistogram（hsv）;

　　imshow（“mapImage”， mapImage）;

　　waitKey（0）;

　　}

　　draw = false;

　　break;

　　//移動(dòng)光標(biāo)

　　case CV_EVENT_MOUSEMOVE：

　　if （draw）

　　{

　　//用MIN得到左上點(diǎn)作為矩形框的起始坐標(biāo)，如果不加這個(gè)，畫(huà)矩形時(shí)只能向一個(gè)方向進(jìn)行

　　rect.x = MIN（x， cursor.x）;

　　rect.y = MIN（y， cursor.y）;

　　rect.width = abs（cursor.x - x）;

　　rect.height = abs（cursor.y - y）;

　　//防止矩形區(qū)域超出圖像的范圍

　　rect &= Rect（0， 0， src.cols， src.rows）;

　　}

　　break;

　　}

　　}

　　int main（）

　　{

　　src=imread（“test.jpg”）;

　　if（！src.data）

　　{

　　cout《《“error， the image is not built！”《《endl;

　　return -1;

　　}

　　cvtColor（src， hsv， CV_BGR2HSV）;

　　//用鼠標(biāo)獲取ROI

　　namedWindow（“SrcImage”）;

　　imshow（“SrcImage”，hsv）;

　　setMouseCallback（“SrcImage”， onMouse， NULL）;

　　waitKey（）;

　　return 0;

　　}12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091

　　運(yùn)行結(jié)果：

　　程序說(shuō)明：

　　程序中涉及反向投影直方圖的代碼就幾行而已，只是因?yàn)橹暗牟┛椭邪阎狈綀D的計(jì)算封裝成了類，就代碼重用了［其實(shí)是懶］！再嘮叨一句，反向投影直方圖的結(jié)果是一個(gè)概率映射，其體現(xiàn)的是已知的圖像內(nèi)容出現(xiàn)在圖像中特定位置的概率。