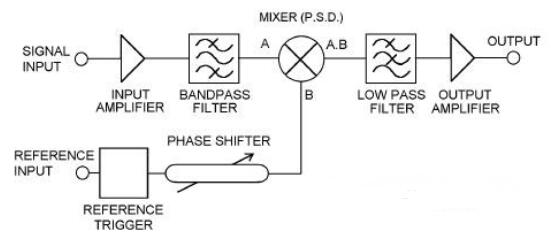
鎖相放大器是一種用于測量動態信號的電子儀器。它的主要組成部分有振蕩器,混頻器和低通濾波器。它的最基本,也是最常用的功能是從被噪聲淹沒的信號中測出某一頻率的信號的相位和幅值。它之所以具備這樣的能力是運用了正交性原理,將非選定頻率的信號(即噪聲)去除而選定頻率的信息得以保留。因為具有很強的抗噪聲能力,鎖相放大器被廣泛應用于各種高精測量系統中,比如MEMS研究。
鎖相放大器降噪原理
鎖相放大器就是利用互相關的原理設計的一種同步相千檢測儀。它是一種對檢測信號和參考信號進行相關運算的電子設備。在測量中,噪聲是一種不希望的擾亂信號,它是限制和影響測量儀器的靈敏度的白噪聲和1/ f 噪聲的低頻噪聲。這些噪聲是無法用屏蔽等措施消除的。為了減少噪聲對有用信號的影響,常用窄帶濾波器濾除帶外噪聲,以提高信號的信噪比。但是,由于一般濾波器的中心頻率不穩,而且帶寬和中心頻率以及濾波器的Q 值有關等原因,使它不滿足更高的濾除噪聲之要求。
根據相關原理,通過乘法器和積分器串聯,進行相關運算,除去噪聲干擾,實現相敏檢波,鎖相放大器采用互相關接受技術使儀器抑制噪聲的性能提高了好幾個數量級。另外,還可以用斬波技術,把低頻以至直流信號變成高頻交流信號后進行處理,從而避開了低頻噪聲的影響。鎖相放大器抑制噪聲的性能如下:國內外生產的鎖相放大器的等效噪聲帶寬厶在103HZ 數量級,少數的可以達可見,儀器具有非常窄的信號和噪聲帶到4X 104Hz,信號帶寬2.55X 106Hz,寬,通常帶通濾波器由于Q 值的定義,常規濾波器很難達到一些性能。
而鎖相放大器被測信號和參考信號是同步的,它不存在頻率穩定性問題,所以可以把它看成為一個“跟蹤濾波器”。它的等效Q 值由低通濾波器的積分時間常數決定,所以對元件和環境的穩定性要求不高。研究表明,鎖相放大器使信噪比提高一萬多倍即信噪比提高了80dB 以上。這足以表明,采用相關技術設計的鎖相放大器具ncin nnm有很強的抑制噪聲能力。
極高的放大倍數,若有輔助前置放大器,增益目前鎖相放大器有如下特點:可達1011(即220dB),能檢測極微弱信號交流輸入、直流輸出,其直流輸出電壓正比于輸入信號幅度及被測信號與參考信號相位差,滿刻度靈敏度達PV、nV 甚至于PV 量級。由此可見,鎖相放大器具有極強的抗噪聲性能。它和一般的帶通放大器不同,輸出信號并不是輸入信號的放大,而是把交流信號放大并變成相應的直流信號。
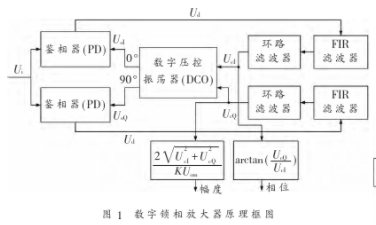
因此,這實際上不符合常規放大器的功能。在國外常把這類儀器稱為鎖相放大器。可理解為把待測信號中與參考信號同步的信號放大并檢測出來。因此,將鎖相放大器稱為“鎖定檢測儀”或“同步檢測儀”或許更為確切。但目前國內都稱為“鎖相放大器”或“鎖定放大器”。鎖相放大器通常分為模擬鎖相放大器和數字鎖相放大器,而兩種類型的L隊各有優缺點。常用的模擬鎖相放大器雖然速度快,但是參數穩定性和靈活性差,且在與微處理器通訊的時候需要轉換電路; 傳統數字鎖相放大器一般使用高速ADC 對信號進行高速采樣,然后使用比較復雜的算法進行鎖相運算,這對微處理器的速度要求很高。
為了大幅度提高檢測下限和測量靈敏度,不僅要減少測量系統的噪聲,而且要能從噪聲中提取信號,故采用的新思路,進行相千檢測。其基本思想是:
1) 首先使測量系統的主要部分,避開噪聲功率密度大的地方,從而使輸入噪聲較小。已知在低頻區,閃爍噪聲可以比自噪聲高出數倍、數十倍、甚至數百倍。因此,要設法使信號不失真的從低頻區移出(1/F 角以外)。
2) 對不同的頻率信號,應該設法將其移頻至固定中心頻率,這樣就可以使用固定中心頻率,固定頻帶的BPF。
3) 從信號與噪聲的特征對比可以看出,信號與多數噪聲有頻率和相位兩個方面的不同。BPF 只是利用頻率特征的識別。因此,如果再利用相位特征的識別,將可把同頻率、不同相位的噪聲大量排除。在光學中,對頻率和相位都進行區分的方法稱為相干法,故這種檢測方法叫相千檢測,在電子學中,這種檢測方法稱為鎖定相位。
為什么鎖相放大器抗噪能力強
鎖相放大器不容易受到噪聲影響的原因,是因為很好地利用了噪聲(白噪聲)與目的信號(正弦波)之間在性質上的差別。在這里,我們一方面整理白噪聲的性質和正弦波的性質,一方面解說為什么鎖相放大器會具有很強的噪聲抑制能力。
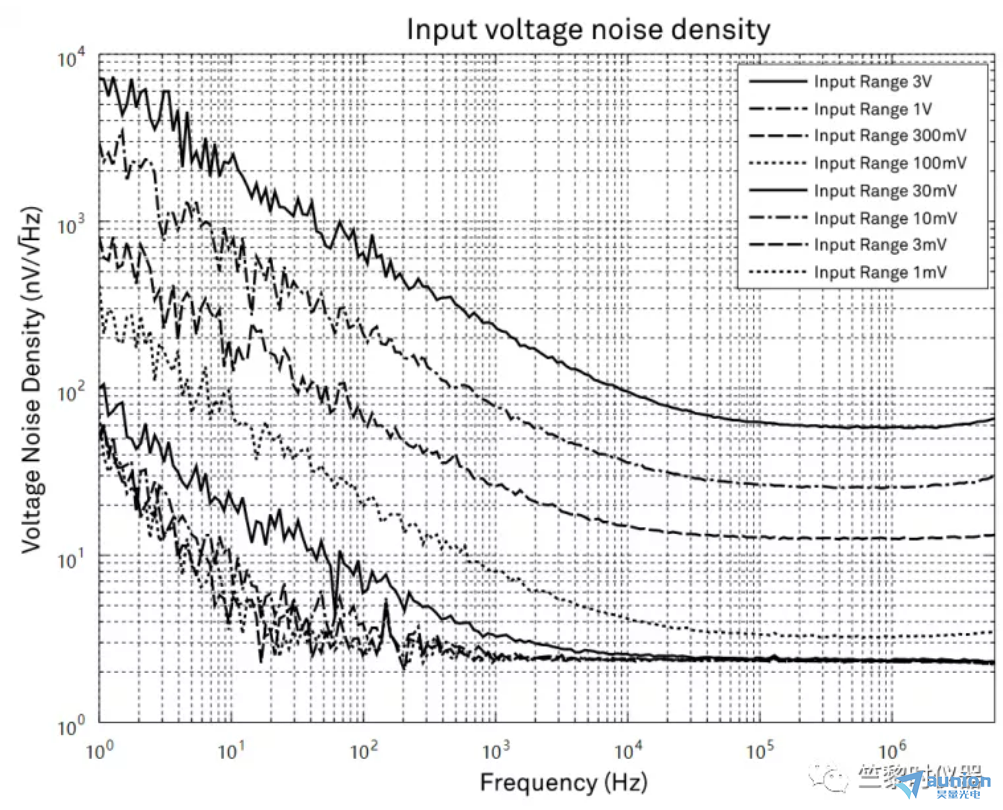
1、平坦的頻譜
在寬闊的頻率范圍內,該信號具有幾乎相同的頻譜。信號的瞬時電平成為預測不到的隨機的值。
2、隨著頻帶寬度不同測量電壓會改變
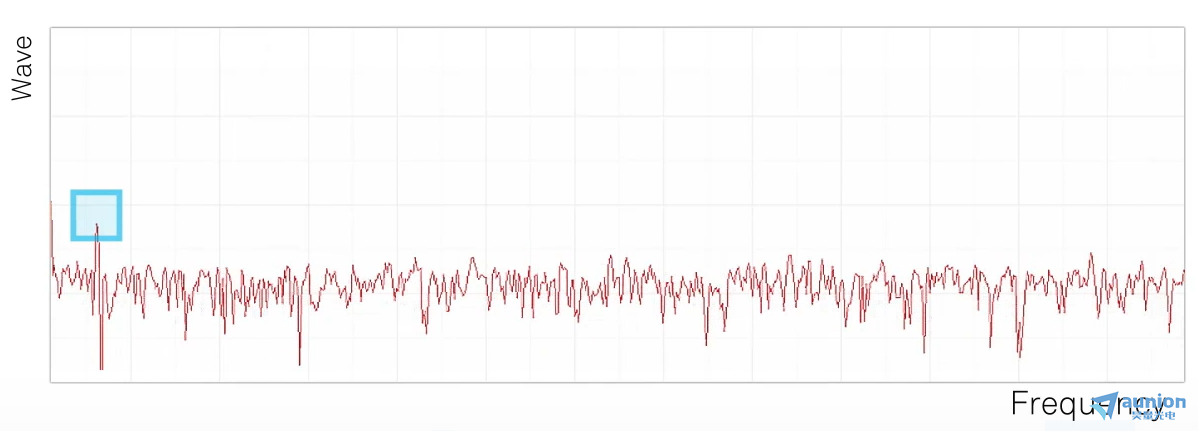
在用毫伏計測量白噪聲時,得到的測量值和白噪聲所具有的頻譜帶寬(BandWidth: B.W.)的平方根以及電平成比例。測量得到的電壓值,與下圖中的淺藍色部分的面積成比例。
即使對于同樣的噪聲,如果用帶通濾波器(BPF)來限制所通過的頻帶,那么測量所得的電壓值就會不同。
把測量所得的噪聲電壓(Vrms),除以頻帶寬度的平方根,就得到用表示噪聲大小的單位、也即稱作噪聲電壓密度(V/√Hz)來衡量的值。頻道寬度如果縮小到1/100,那么測量所得的噪聲電壓就縮小到1/10。
3、頻譜非常集中
1kHz正弦波信號的頻譜,只存在于1kHz的位置,其他地方的頻譜的電平都為零。
4、與頻帶寬度無關,測量所得電壓保持一定的值
因為頻譜是集中分布的,所以不受頻帶寬度的影響,測量所得的電壓保持一定的值。但是,必須要使信號頻率存在于所取的頻帶之內。用交流電壓表所測量的電壓值,與頻帶寬度無關,是上圖中的V。那么,在正弦波上疊加了白噪聲以后會怎么樣呢?
即使白噪聲與正弦波進行加法運算所得的信號,測量所得的電壓對于頻帶寬度所具有的各種性質也不會有變化。所以,當帶通濾波器的頻帶寬度變狹窄時,就會有以下結果:
想要測量的信號的電平不變;白噪聲的強度減小;交流聲等頻率不同的成分也當然被削弱。
從以上這些結果可知,為了測量被噪聲所掩埋的信號,應該將帶通濾波器的頻帶寬度變窄。如果將頻帶寬度縮小到1/N,那么噪聲就減小到1/√N,而信號卻不改變,其結果SN比(信噪比)改善為1/√N。
但是,這樣的帶通濾波器也是有一個限度的。為了說明「鎖相放大器利用了噪聲與目的信號所具有的不同性質,所以不容易受到噪聲的影響」,前面已解說了以下幾個要點:
噪聲(白噪聲)的性質;正弦波的性質;從白噪聲與正弦波合成的信號中,使用帶通濾波器可以使目的信號(正弦波)從噪聲中浮現出來。
5、使通帶變狹窄的限度
使用帶通濾波器只讓想要測量的頻率信號通過,可以抑制噪聲,讓目的信號浮現出來。但是,使帶通濾波器的通帶寬度變窄,這也是有限度的。
在帶通濾波器中,中心頻率與通帶寬度的比值稱作Q值,作為衡量帶通濾波器的濾波尖銳程度的一項指標來使用。
Q值越大,通帶寬度就越窄,抑制噪聲的能力就越強。但是,一般的濾波器所能夠實現的Q值,大約在100左右。對于1kHz的中心頻率,相應的通帶寬度的限界大約在10Hz左右。Q值不能任意增大的原因,在于組成濾波器的零部件的精確度和時間/溫度的穩定性是有限的。

 電子發燒友App
電子發燒友App























評論