十進制數的編碼與運算

　　十進制數的每一個數位的基為10，但到了計算機內部，出于存儲與計算方便的目的，必須采用基2碼對每個十進制數位進行重編碼，所需要的最少的基2碼的位數為log210，取整數為4。4位基2碼有16種不同的組合，怎樣從中選擇出10個組合來表示十進制數位的0-9，有非常多的可行方案，下面介紹其中的最常用的幾種。

　　① 十進制有權碼
　　是指表示一個十進制數位的4位基2碼的每一位有確定的位權。
　　用得最普遍的是8421碼，即4個基2碼位的權從高向低分別為8、4、2和1，使用基2碼的0000、0001、…1001這10種組合，分別表示0到9這十個值。這種編碼的優點是這4位基2碼之間滿足二進制的規則，而十進制數位之間則是十進制規則，故稱這種編碼為以二進制編碼的十進制(Binary Coded Decimal)數，簡稱BCD碼或二-十進制碼。另一個優點是在數字符的ASCII碼與這種編碼之間的轉換方便，即取每個數字符的ASCII碼的低4位的值便直接得到該數字的BCD碼，入/出操作簡便。在計算機內實現BCD碼之間的算術運算要復雜一些，在某些情況下，需要對加法運算的結果進行修正。修正規則是:

　　若兩個8421碼數相加之和等于或小于1001，即10進制的9，不需要修正；
　　若相加之和在10到15之間，一方面應向高位產生一進位，本位還要進行加6修正，進位是在進行加6修正時產生的；
　　若相加之和在16和18之間時，向高位的進位會在相加過程中自己產生，對本位還需進行加6修正。下面給出三種情況下的具體例子。

　　例如，1+8=9的運算結果是正確的，不必修正。

　　　　0 0 0 1
　　　+)1 0 0 0 　　　(1)₁₀+(8)₁₀=(9)₁₀
　　
　　　　1 0 0 1

　　而4+9的結果就必須用 +6 修正，進位是在修正過程中產生的。

　　　　0 1 0 0
　　　+)1 0 0 1 　　　(4)₁₀+(9)₁₀ =（1）₁₀ (3)₁₀
　　
　　　　1 1 0 1
　　+） 0 1 1 0
　　
　　　1 0 0 1 1

　　而7+9的結果也必須用 +6 修正，進位是在相同加過程中產生的。

　　　　0 1 1 1
　　　+)1 0 0 1 　　　(7)₁₀+(9)₁₀ =（1）₁₀(6)₁₀
　　
　　　1 0 0 0 0
　　+） 0 1 1 0
　　
　　　1 0 1 1 0

　　另外幾種有權碼,如2421、5211、84-2-1、4311碼(表2.9),也都是用4位有權基2碼表示一個十進制數位，但這4位基2碼之間并不符合二進制規則。這幾種有權碼的特性表現為:

　　當采用2421、5211和4311編碼時,任何兩個十進制數位相加產生10或大于10的結果,相應的基2碼相加會向高一位產生進位,有利于實現逢十進位的計數和加法規則。

　　任何兩個相加之和等于9的十進制數位的基2碼，互為反碼，即滿足十進制數按9互補(9's Complement)的關系，有利于簡化減法處理。表2.9給出的是上面提到的十進制數位的編碼方案。

表2.9 四位有權碼

十進制數	8421碼	2421碼	5211碼	840201碼	4311碼

　② 十進制無權碼

　　是指表示一個十進制數位的4位基2碼的每一位沒有確定的位權。

　　在采用的無權碼的一些方案中，早期用的比較多的是余3碼（Excess-3 code），是把原二進制的每個代碼都加0011值得到的。它的主要優點是執行十進制數位相加時,能正確地產生進位信號，而且還給減法運算帶來了方便。

　　采用余3碼執行加法運算的規則是:
　　當兩個余3碼相加不產生進位時,應從所得結果中減去0011；
　　產生進位時,一方面應將進位信號送入高位余3碼，本位還應執行加0011的修正操作。例如:

　　(1) 　　0101 0011 　　　（20）₁₀+（75）₁₀= （95）₁₀
　　　　+） 1010 1000
　　　　
　　　　　　1111 1011
　　　　-） 0011 0011
　　　　
　　　　　　1100 1000

　　(2) 　　0101 1011 　　　（28）₁₀+（55）₁₀=（83）₁₀
　　　　+） 1000 1000
　　　　
　　　　　1101 1 0011
　　　　　1110
　　　 -）0011 + 0011
　　　　
　　　　　1011 　0110

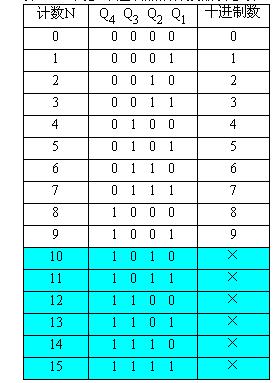
　　格雷碼是另外一種常用的二-十進制編碼，是使任何兩個相鄰的代碼只有一個二進制位的狀態不同，其余三個二進制位必須有相同狀態。這種編碼方法的好處是，從一編碼變到下一個相鄰編碼時，只有一位的狀態發生變化，有利于得到更好的譯碼波形，在模擬→數字、數字→模擬轉換的電路中得到更好的運行結果。用四個二進制位的格雷碼表示十進制數的十個狀態的方案很多。表2.10給出兩組最常用的編碼值。

表2.10 四位無權碼

十進制數	余三碼	格雷碼（1）	格雷碼（2）

③ 十進制數的其它編碼方法

　　也有用多于4位基2碼,如用5位、7位、甚至10位基2碼，來表示一個十進制數位的方案。有些屬于無權碼，有些屬于有權碼。表2.11給出4種編碼方案。

表2.11 十進制數位編碼方案

十進位	無權碼		有權碼
符號	五中取二碼	蠕變碼	二元五進制碼 5043210	獨熱碼 0123456789

　　五中取二碼 (2-out-of-5 Code)使用5位基2碼，并且每個代碼必須包含2個"1"和3個"0"，因此提供了一位（或奇數位）檢粗能力。

　　蠕變碼（Creeping Code）也用5位基2碼，是由一個"1"逐次移位擴展和收縮而形成的，符合格雷碼的編碼規則。
④ 數字串在計算機內的表示與存儲

　　人們習慣使用10進制數，而在計算機內，采用二進制表示和處理數據更方便。因此,在計算機輸入和輸出數據時，要進行十→二和二→十的進制轉換處理，這是多數應用環境中的實際情況。而在某些特定的應用領域中，如商業統計，其特點是運算簡單而數據量很大，這樣使輸入輸出過程中的進制轉換所占的時間比例很大。從提高機器的運行效率考慮，也可以采用在計算機內部直接用十進制方式表示和處理數據，這要求計算機內部增加少量硬件線路。目前，大多數通用性較強的計算機，都能直接處理十進制形式表示的數值。采用十進制表示數據的另一個目的，是提高數據的表示范圍和運算精度，就是說，十進制數在計算機內是以十進制的數位組成的數串形式存儲與計算的，其位數，即串長是可變的，可規定最長可用位數，因此不受二進制整數和浮點數統一格式的約束。

　　十進制數串在計算機內主要有兩種表示形式。
　　a. 字符串形式,即一個字節存放一個十進制的數位或符號位。在主存中，這樣的一個十進制數占用連續的多個字節，故為了指明這樣一個數，需要給出該數在主存中的起始地址和位數(串的長度)。

　　對用這種方式表示的數據進行算術運算是很不方便的，因為每個數字符占用一個字節，其低四位的值表示數值，而高四位的值在進行算術運算時不具有數值的意義。因此，用這種方式表示的十進制字符串，主要用在非數值計算的有關應用領域中。

　　b. 壓縮的十進制數串形式，即一個字節存放兩個十進制的數位，它比前一種形式節省存儲空間，又便于直接完成十進制數的算術運算，是廣泛采用的較為理想的方法。

　　用壓縮的十進制數串表示一個數，要占用主存連續的多個字節，每個數位占用半個字節(即4個二進制位)，其值可用二-十進制編碼(BCD碼，數字符的ASCII碼的低4位)表示,符號位也占用半個字節并存放在最低數字位之后，其值選用四位編碼的六種冗余狀態中的有關值，如用1100表示正號，用1101表示負號。在這種表示中，規定數值位加符號位之和必須為偶數，當其和不為偶數時，應在最高數字位之前補一個0。此時,表示一個數要占用該偶數值位的一半那么多個字節。例如:
　　　　　　　　　　　+123被表示成 123C， -12 被表示成 012D。

　　要指明一個壓縮的十進制數串，也需給出它在主存中的首地址和數字位個數(不含符號位)，又稱位長，位長為0的數其值為0。壓縮的十進制數串表示方法的優點是位長可變，許多機器中規定該長度從0到31，有的甚至更長。