十進制計數器

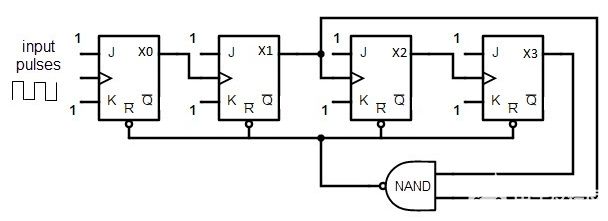
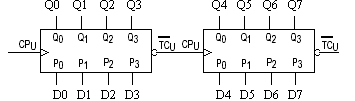
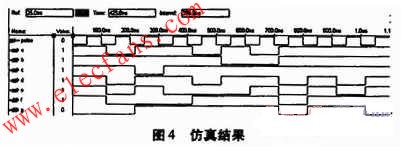
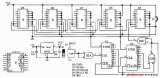
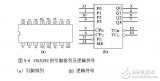
二進制計數器具有電路結構簡單、運算方便等特點，但是日常生活中我們所接觸的大部分都是十進制數，特別是當二進制數的位數較多時，閱讀非常困難，還有必要討論十進制計數器。在十進制計數體制中，每位數都可能是0，1，2，…，9十個數碼中的任意一個，且“逢十進一”。根據計數器的構成原理，必須由四個觸發器的狀態來表示一位十進制數的四位二進制編碼。而四位編碼總共有十六個狀態。所以必須去掉其中的六個狀態，至于去掉哪六個狀態，可有不同的選擇。這里考慮去掉1010～1111六個狀態，即采用8421BCD碼的編碼方式來表示一位十進制數。 8.5.1 8421BCD碼異步十進制加計數器: 用JK主從觸發器組成的一位異步十進制加計數器如圖8.5.1(a)所示。 1.電路結構: 由四個JK主從觸發器組成，其中FF0始終處于計數狀態。Q0同時觸發FF1和FF3，Q3反饋到J1，Q2Q1作為J3端信號。 2.工作原理 (1)工作波形分析法由邏輯圖可知，在FF3翻轉以前，即從狀態0000到0111為止，各觸發器翻轉情況與異步二進制遞增計數器相同。第八個脈沖輸入后，四個觸發器狀態為1000，此時Q3＝0，使下一個FF0來的負階躍電壓不能使FF1翻轉。因而在第十個脈沖輸入后，觸發器狀態由1001變為0000，而不是1010，從而使四個觸發器跳過1010～1111六個狀態而復位到原始狀態0000，其工作波形如圖8.5.1(b)所示。

當第十個脈沖作用后，產生進位輸出信號C0=Q3Q0。

(2)狀態方程分析法: 首先列出各觸發器驅動方程：

觸發器在異步工作時，若有CP觸發沿輸入，其狀態由特征方程確定，否則維持原態不變。這時觸發器的特征方程可變為Qn+1=(JQn+KQn)CP↓+QnCP↓，其中CP↓＝1表示有CP觸發沿加入，CP＝0表示沒有CP觸發沿加入。所以可以寫出以下狀態方程：

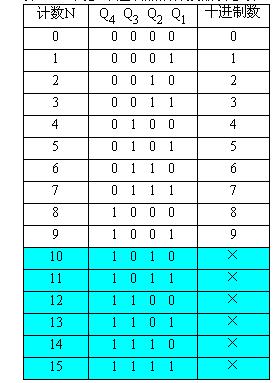
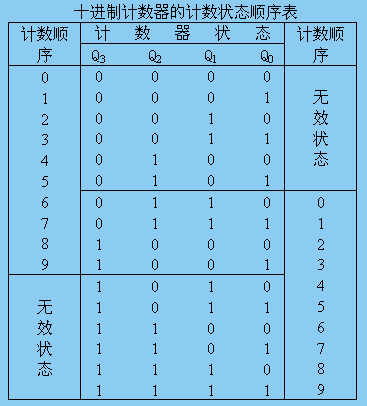
根據以上狀態方程，即可列出計數器的狀態轉移表，如表8.5.1所示。表8.5.1 異步十進制加計數器的狀態轉移表

以上兩種方法均表明該邏輯電路具有8421碼異步十進制遞增計數的功能。

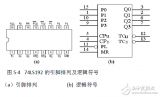
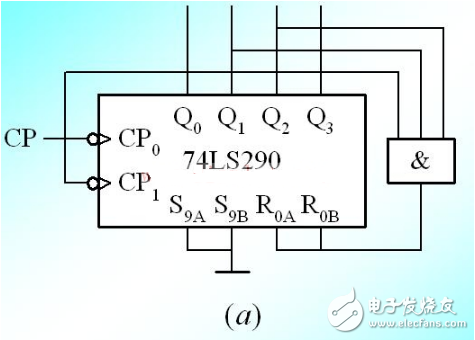
8.5.2 8421碼同步十進制加計數器: 1.電路結構如圖8.5.2所示，由四個主從JK觸發器組成，各觸發器共用同一個計數脈沖，是同步時序邏輯電路。

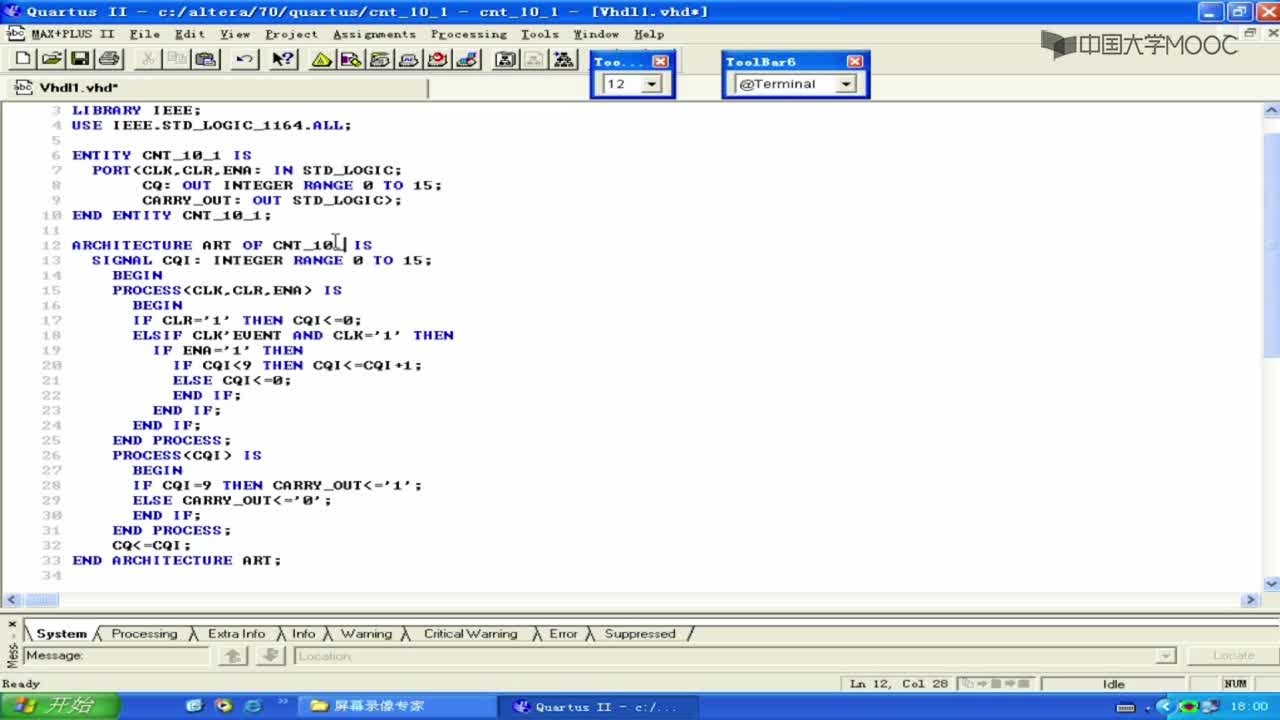
2.工作原理: 各觸發器方程：

由于各觸發器共用同一個時鐘脈沖，故上式中的CP↓可忽略不寫。 (3)列狀態轉移表設計數器狀態為Q3Q2Q1Q0＝0000，根據狀態方程可列出狀態轉移真值表，該表與表8.5.1相同（不包括CP部分）。所以該電路是8421碼十進制遞增計數器。