一般有兩種形式，一種是 有源濾波器（抗混疊濾波器）+RC（用于給ADC內部保持電路提供電荷緩沖） 另一種是 單RC濾波器；
2023-10-16 12:29:08
535 
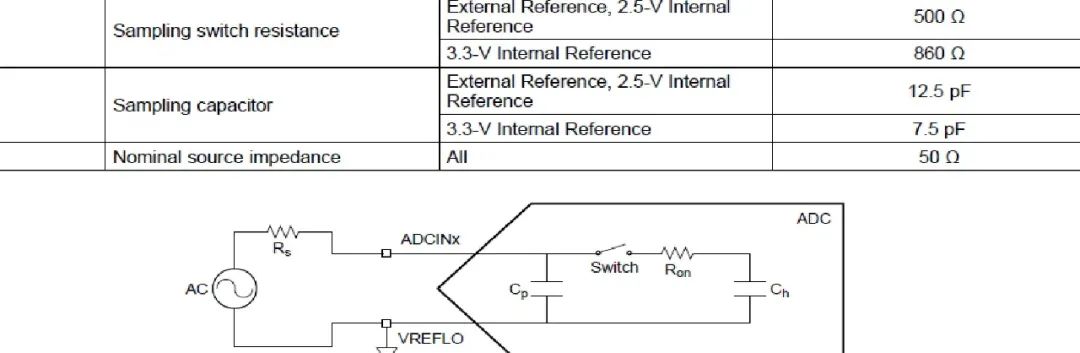
引言：感謝“八塊腹肌餅干”的邀約，針對無源濾波器專門更新幾期，先從RC開始吧。簡單基本RC電路有一些非常有用的特性，既能提供相當精確可重復的定時功能，又能很好的執行基本的濾波功能，本節簡述基本的RC濾波器特性。?
2023-09-14 15:45:37246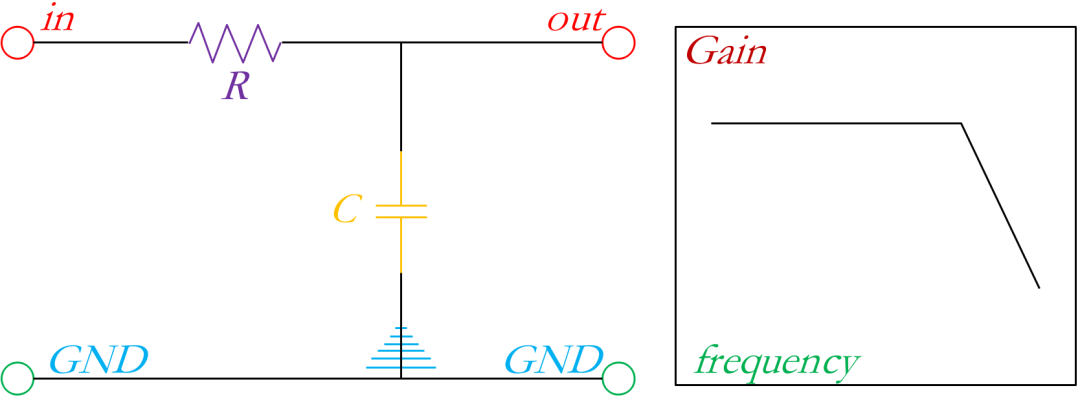 
為什么串上電容是高通濾波器？串上電阻是低通濾波器呢？? 濾波器在電子工程中是一個重要的概念，它可以幫助我們從信號中分離出我們所需的部分，并去除我們所不需要的部分。在濾波器的設計中，電容和電阻是最常
2023-09-13 10:01:50314 非常重要。 以下是選擇SAR ADC前端RC濾波器的一些關鍵因素： 1. 帶寬和采樣率 前端的濾波器應該能夠過濾掉不需要的高頻信號，以確保ADC的輸出僅包含所需的信號，并且完整而清晰。選擇濾波器的截止頻率應該低于系統帶寬的一半，以確保信號的完整性。對于SAR ADC而言，采樣率
2023-09-13 10:01:45116 rc濾波器電阻電容如何選擇？? RC濾波器是一種基本的電子電路。這種電路由電阻和電容組成，能夠降低輸入信號中的高頻分量，達到濾波的效果。在實際設計中，正確選擇電阻和電容的數值是很重要的，本文將介紹
2023-09-13 10:01:32599 在測試系統中，通常使用RC濾波器。因為在這個區域，信號頻率比較低。RC濾波器具有電路簡單，抗干擾性強，低頻性能更好，選用標準電阻電容元件等優點。所以工程測試領域最常用的濾波器是RC濾波器。
2023-07-03 11:53:584729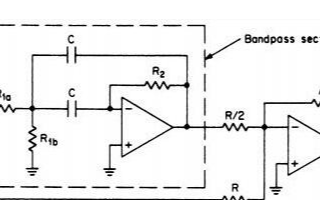 
高通濾波器和低通濾波器是根據信號頻率通過或被阻斷的不同而得名的。在電子工程中，有時需要對信號進行濾波以去除噪聲或將特定頻率范圍內的信號傳輸到輸出端。下面介紹一些判斷高通濾波器和低通濾波器的方法。
2023-06-26 09:33:301165 本帖最后由 gk320830 于 2015-3-7 18:01 編輯
1．濾波器是對輸入信號的頻率具有選擇性的一個二端口網絡，它允許某些頻率（通常是某個頻率范圍）的信號通過，而其它頻率的信號幅
2008-09-24 11:13:01
對于無源 RC 微分器電路，輸入連接到電容器，而輸出電壓取自與 RC 積分器電路完全相反的電阻兩端。
2023-05-09 09:06:461412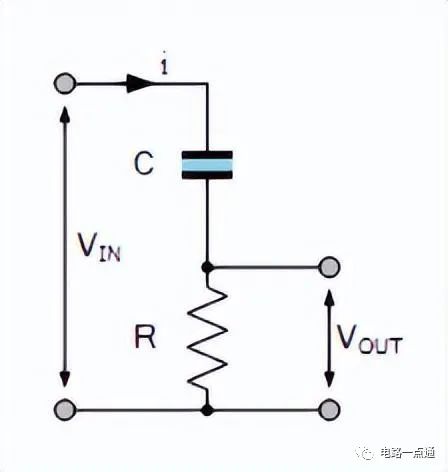 
高通濾波器是一種濾波器，它可以抑制低頻信號，使高頻信號通過。它的基本信息包括截止頻率、衰減率和增益。截止頻率是指濾波器的最高頻率，衰減率是指濾波器的衰減率，增益是指濾波器的增益。
高通濾波器
2023-02-26 16:14:271392 RC高通濾波器。當信號通過RC高通濾波器時，低于一定頻率的信號會被電容器阻塞，從而被濾除，只有高于該頻率的信號能夠通過電容器和電阻。
2023-02-25 16:06:465650 高通濾波器和低通濾波器是互補的，它們可以組合使用，從而實現更復雜的濾波功能。例如，可以將高通濾波器和低通濾波器組合在一起，從而實現帶通濾波器的功能。
2023-02-17 17:47:172289 要將低通濾波器改為高通濾波器，可以改變濾波器的電路結構，將電容和電感的位置互換，即將電容放在輸入端，電感放在輸出端，這樣就可以將低通濾波器改為高通濾波器。
2023-02-17 17:26:281387 低通濾波器和高通濾波器的不同之處在于，低通濾波器的電路結構中，電容放在輸出端，電感放在輸入端，而高通濾波器的電路結構中，電容放在輸入端，電感放在輸出端。此外，低通濾波器可以抑制高頻信號，而高通濾波器可以抑制低頻信號。
2023-02-17 14:50:217321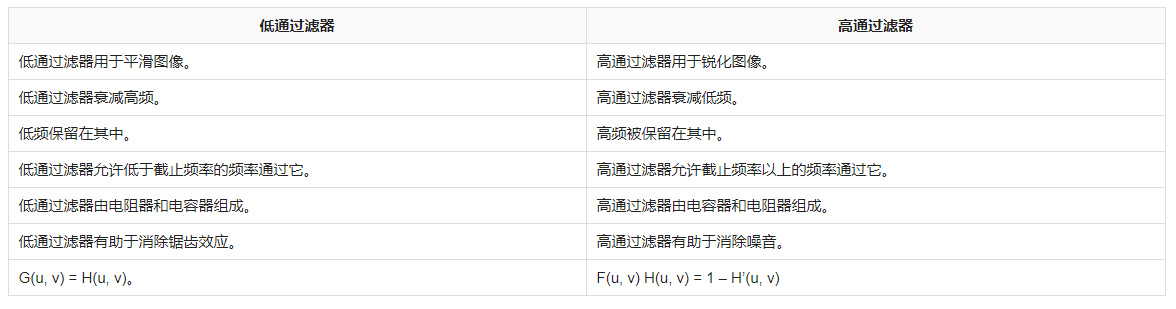 
低通濾波器和高通濾波器的主要區別在于：低通濾波器能夠通過低頻信號，而高通濾波器能夠通過高頻信號；低通濾波器能夠抑制高頻信號，而高通濾波器能夠抑制低頻信號。
2023-02-17 14:21:4411599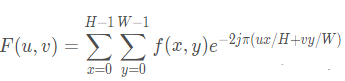 
高通濾波器的帶寬是指濾波器在頻率范圍內，信號的衰減程度小于一定程度的頻率范圍。高通濾波器的帶寬是指濾波器在頻率范圍內，信號的衰減程度小于-3dB時的頻率范圍。一般來說，高通濾波器的帶寬越寬，濾波器的性能越好。
2023-02-16 11:04:291795 高通濾波器的幅頻特性指的是濾波器在不同頻率處的衰減量，它可以用來衡量濾波器的性能。一般來說，高通濾波器的幅頻特性是一條從低頻到高頻，衰減程度逐漸增大的曲線。高通濾波器的幅頻特性越平緩，濾波器的性能越好。
2023-02-16 10:38:334703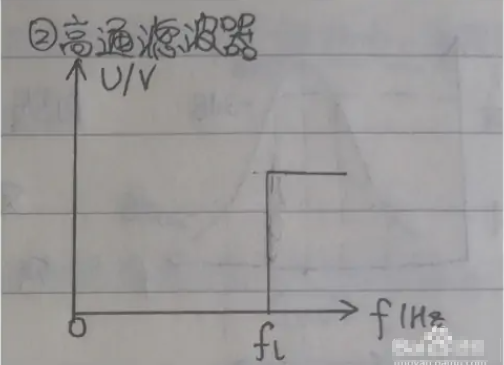 
π型濾波器是一種雙極濾波器，它由兩個RC組件組成，其中一個RC組件是濾波器的輸入端，另一個RC組件是濾波器的輸出端。當信號通過濾波器時，輸入端的RC組件會把低頻信號通過，而高頻信號則會被抑制。因此，π型濾波器可以用來抑制高頻信號，從而實現信號的濾波。
2023-02-16 10:02:117838 導讀：本期文章主要介紹一階高通濾波器。一階高通濾波器與一階低通濾波器很相似，都是利用電容阻低頻信號通高頻信號，電感阻高頻信號通低頻信號的特點。
2023-01-29 16:03:323355 電子電路設計中，常用的濾波器主要分為高通濾波器、低通濾波器、帶阻濾波器、帶通濾波器，而這四種濾波器又統稱為有源濾波器。下面單獨談一下這個高通濾波器的工作原理與運用。
2022-12-19 10:46:004484 電子發燒友網站提供《低通濾波器RC項目.zip》資料免費下載
2022-11-08 11:21:28
1 本文介紹了濾波的概念，并詳細說明了電阻 - 電容（RC）低通濾波器的用途和特性。
2022-11-06 22:23:222247 作為一個電子硬件方面的工作者,怎么能不認識濾波器呢?那么到底什么是濾波?分享一篇科普文~了解一下電阻 - 電容(RC)低通濾波器是什么以及在何處使用它們能讓你更好的掌握高端的電路設計實戰。本文將介紹了濾波的概念，并詳細說明了電阻 - 電容(RC)低通濾波器的用途和特性。
2022-11-06 19:49:593152 濾波器是一種電路，旨在抑制電信號中所有不需要的頻率分量，只允許所需的頻率。換句話說，濾波器是一種只允許特定頻帶的電路。
2022-09-12 14:15:0013505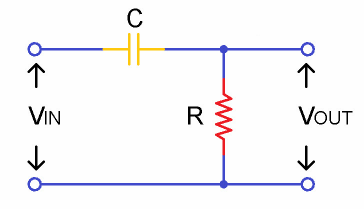 
而無源RC濾波器當然是大部分濾波器中首選的廉價設計，并且能較簡單數字化為軟件濾波器設計，所以軟件與硬件濾波在于一個離散數字化的過程，所以整體設計上大同小異。
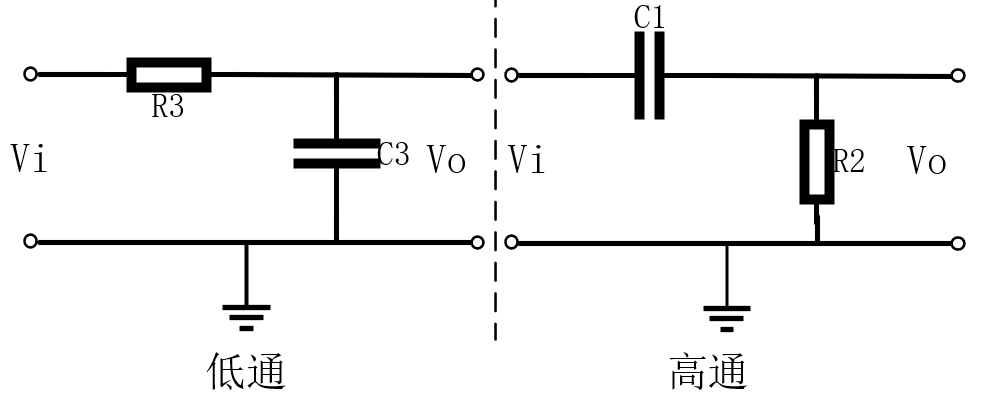
2022-09-06 09:37:221767 這個比較簡單，用一個電阻和電容構成的濾波器稱為無源濾波器，根據結構的不同可分為低通濾波器和高通濾波器，分別如下圖所示。
2022-08-10 15:40:3210155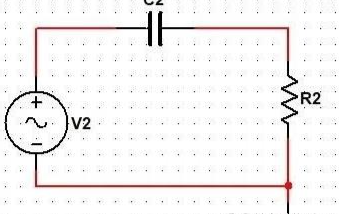 
讓我們一起來看看處理EMC問題中最常用的手段-RC濾波。
本文介紹了濾波的概念，并詳細說明了電阻電容（RC）低通濾波器的用途和特性。
2022-07-21 15:17:372 本文以實際的幅值計算，來推理出RC低通濾波器的原理，又引入相移的思考方向，值得看一看。
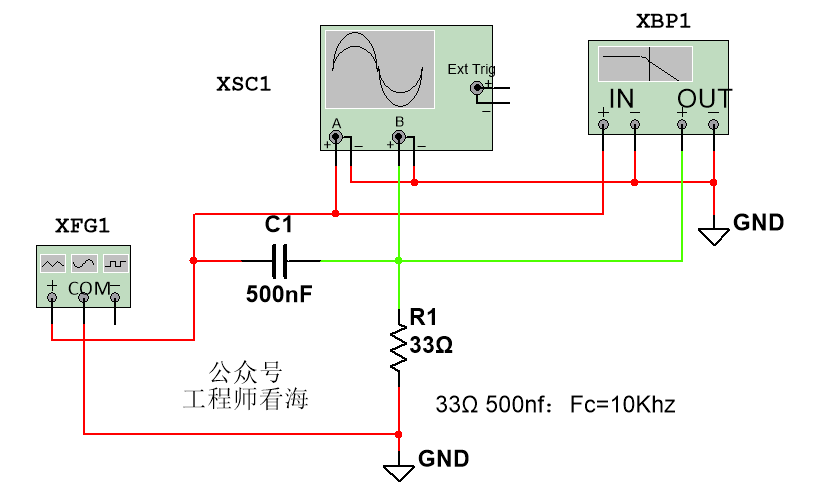
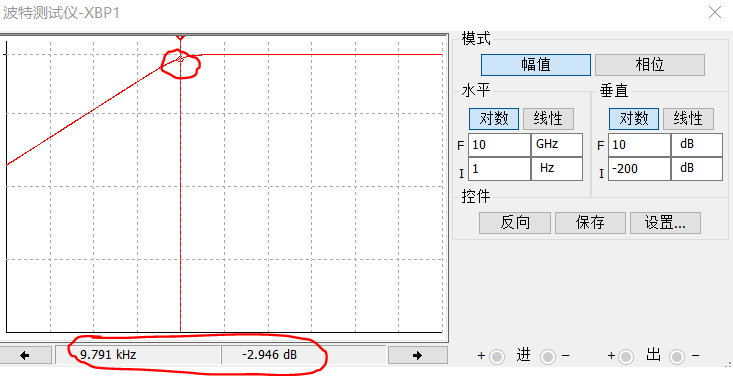
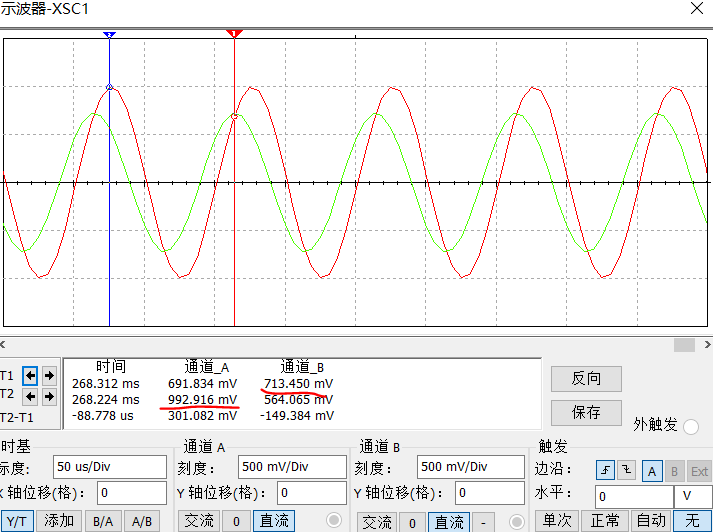
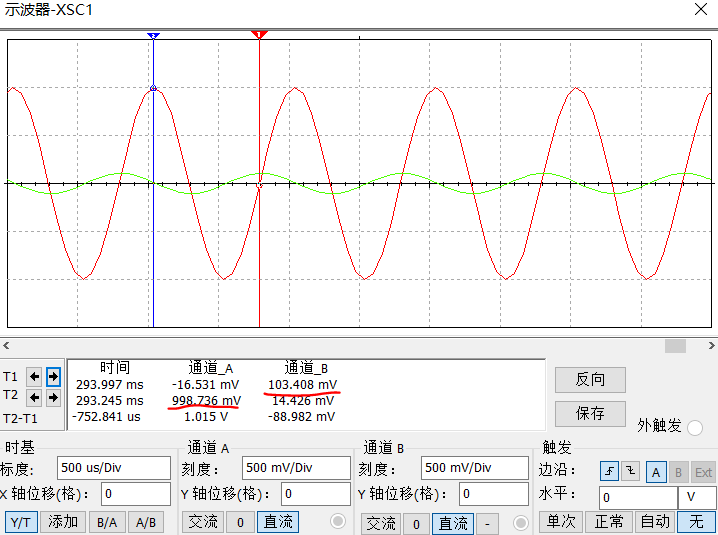
2022-07-04 16:33:0417572 原文來自公眾號：工程師看海 在數據采集領域，RC濾波器是最常見的信號調理電路，以前我介紹過RC低通濾波器，今天介紹下與之對應的RC高通濾波器，二者結構對比見下圖。 RC高通濾波器用于抑制低頻干擾或
2022-01-24 09:47:425835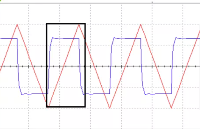 
=1/(2πRC)Hz，允許低于Fc Hz的信號通過，高于Fc Hz的信號不通過， 一階RC濾波器過渡帶比較寬，信號不會衰減的那么劇烈。 然而我們也聽說過 RC積分器，它的結構和RC低通濾波器是完全一樣的，二者參數有什么區別呢？什么時候是低通濾波器？什么時
2021-09-22 09:24:336919 
RC濾波器和LC濾波器的區別 1.LC濾波器應用的頻率范圍為1kHz～1.5GHz.由于受限于其中電感的Q值，頻率響應的截至區不夠陡峭。 2, RC濾波器有耗損，LC濾波器理論上可以無耗損; 3
2021-07-09 16:40:177389 RC濾波器和LC濾波器的區別 1.LC濾波器應用的頻率范圍為1kHz～1.5GHz.由于受限于其中電感的Q值，頻率響應的截至區不夠陡峭。 2, RC濾波器有耗損，LC濾波器理論上可以無耗損; 3
2021-05-07 17:56:485604 本文檔的主要內容詳細介紹的是用于MF RC500和SL RC400的EMC濾波器和阻抗匹配。
2021-03-05 15:34:009 作為一個電子硬件方面的工作者,怎么能不認識濾波器呢？那么到底什么是濾波？分享一篇科普文~了解一下電阻 - 電容（RC）低通濾波器是什么以及在何處使用它們能讓你更好的掌握高端的電路設計實戰。本文將介紹
2021-01-25 07:48:5915 RC濾波器又名RC電路， 是一個包含利用電壓源、電流源驅使電阻器、電容器運作的電路。LC濾波器又稱無源濾波器，是利用電感、電容和電阻的組合設計構成的濾波電路。那RC濾波器和LC濾波器有哪些區別？
2020-12-26 06:53:291579 高通濾波器和低通濾波器區別是高通濾波器是允許信號中的高頻或者交流分量通過，抑制低頻或者直流分量的濾波器。
2020-08-12 16:57:2837625 一種由RC電路和運算放大器構成的低通濾波器，由于運算放大器是有源元件，故稱為有源濾波器。
2020-07-24 14:42:543511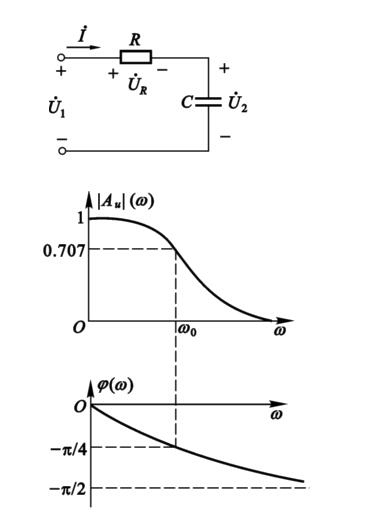 
的參考資料，但寬帶的高通濾波器很少見到簡單高效的設計方法，這里用一個2GHz超寬帶高通濾波器實例米說明懸置線高通濾波器的設計原理和方法。
2020-07-17 10:26:003 如何選擇SARADC前端的RC濾波器
2019-08-21 06:02:004457 RC 濾波器的幅頻特性和相頻特性進行分析。然后對轉折頻率ωC =1000rad/s 的情形分別提出一個一階RC 無源低、高通濾波器和一個二階RC 無源低通濾波器的學生實驗設計方案，對所設計的方案進行頻率特性的研究。
2019-07-09 17:52:4623 無源RC微分器是串聯的RC網絡，其產生對應于微分的數學過程的輸出信號。對于無源RC微分電路，輸入連接到電容輸出電壓來自與 RC積分電路完全相反的電阻。
2019-06-27 16:43:5710999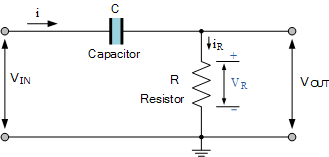 
通過將無源RC濾波器網絡與運算放大器組合以產生具有放大的高通濾波器，可以創建有源高通濾波器，與之前的有源低通濾波器電路一樣，有源高通濾波器的最簡單形式是將標準反相或非反相運算放大器連接到基本RC高通無源濾波器電路
2019-06-27 11:30:3924805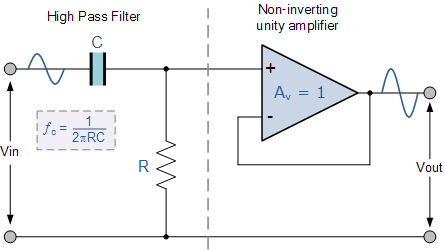 
通過將基本RC低通濾波器電路與運算放大器相結合，我們可以創建一個有放大的有源低通濾波器電路，在RC無源濾波器教程中，我們看到了一個基本的一階濾波器電路，例如低通濾波器和高通濾波器，只需使用一個電阻串聯，并與連接在正弦輸入信號上的非極化電容串聯
2019-06-27 11:12:1634179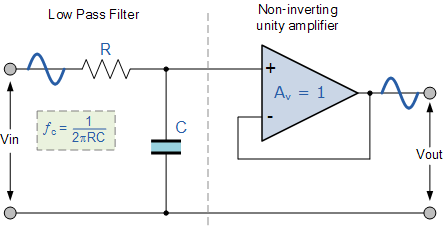 
本文開始闡述了RC微分電路的定義和RC微分電路的特點，其次詳細介紹了RC微分電路的工作原理，最后介紹了RC微分電路的作用以及相關電路圖。
2018-03-27 15:10:37105377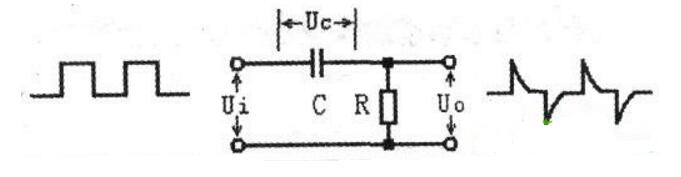 
在測試系統中，常用RC濾波器。因為在這一領域中，信號頻率相對來說不高。而RC濾波器電路簡單，抗干擾性強，有較好的低頻性能，并且選用標準的阻容元件易得，所以在工程測試的領域中最經常用到的濾波器是RC濾波器。
2018-02-26 17:56:1717583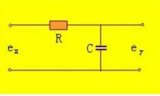 
濾波器。高通濾波器與低通濾波器特性恰恰相反。另外請參見帶通濾波器。 一、高通濾波器的應用 這樣的濾波器能夠把高頻率的聲音引導至專用高音喇叭(tweeter)，并阻止可能干擾或者損害喇叭的低音信號。使用線圈而不是電容的低
2017-11-23 05:58:035939 由RC元件與運算放大器組成的濾波器稱為RC有源濾波器，其功能是讓一定頻率范圍內的信號通過，抑制或急劇衰減此頻率范圍以外的信號。可用在信息處理、數據傳輸、抑制干擾等方面，但因受運算放大器頻帶限制，這類濾波器主要用于低頻范圍。
2017-11-22 16:17:1926723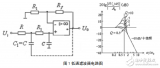 
濾波器主要用來濾除信號中無用的頻率成分，例如，有一個較低頻率的信號，其中包含一些較高頻率成分的干擾。濾波過程如圖13.02所示。 而帶通濾波器是由低通RC環節和高通RC環節組合而成的。要將高通的下限
2017-09-14 11:41:4836 實驗目的
1. 深刻理解 RC 有源濾波器的工作原理。
2. 掌握有源濾波器的測量和調試技術。
2016-10-11 17:41:5937 本實驗方案主要是針對由
R、C 組成的無源濾波器進行介紹，對各種無源 RC 濾波器的幅頻特性和相頻特性進行分析。
然后對轉折頻率 ωC =1000rad/s 的情形分別提出一個一階 RC 無源低、高通濾波器和一個二
階 RC 無源低通濾波器的學生實驗設計方案，對所設計的方案進行頻率特性的研究。
2016-01-14 16:26:3814 精密SAR模數轉換器的前端放大器和RC濾波器設計
2016-01-07 15:08:2325 本文介紹用RC多相濾波器實現鏡像抑制的原理，推導出電阻電容誤差對鏡像抑制影響的數學表達式，通過仿真驗證表明，計算值與仿真值較為接近，并應用RC 多相濾波器來實現高鏡像抑
2011-08-23 14:51:1446 詳細介紹了常用的 RC有源濾波器 的兩種結構及其設計步驟．以第一種VCVS結構為例，設計了基于巴特沃斯逼近的帶通濾波器，并介紹了一款最新的常用的電子設計和仿真軟件Multi．sire
2011-06-16 10:45:03115 摘要：本文提出了采用有源電流傳送器(cc)和Rc濾波器的綜合方法，給出了二階低通、帶通、高通、陷波濾波器以及幅度和相位均衡器的CC—RC實現，這些電路均具有高輸入阻抗、低無
2010-05-30 09:23:2834 VCVS高通濾波器電路原理及函數
將低通濾波器的低通網絡中電阻和電容互換，即得高通濾波器，如
2010-05-23 12:47:334955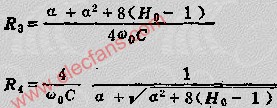 
實用高通濾波器電路
2009-12-07 12:15:094503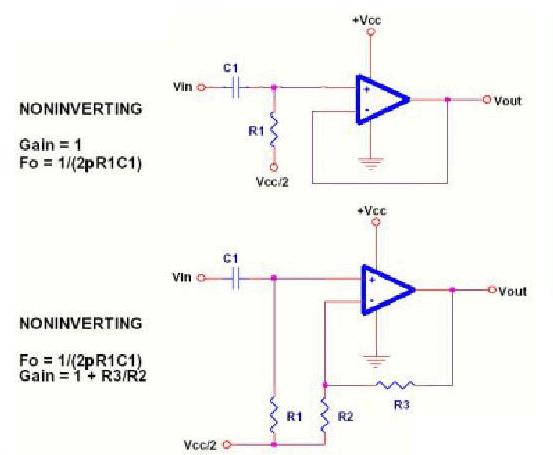 
高通濾波器(微分器)電路
該電
2009-12-07 11:58:523108 
RC濾波器濾波器是一種通過一定頻率的信號而阻止或衷減其余頻率信號的電路。它的應用十分廣泛，從簡單的半導體收音機到復雜的電子設備幾乎都使用著各種形式的濾波器。電
2009-09-22 09:49:27263 雙象限RC帶通濾波器
2009-09-17 15:11:22809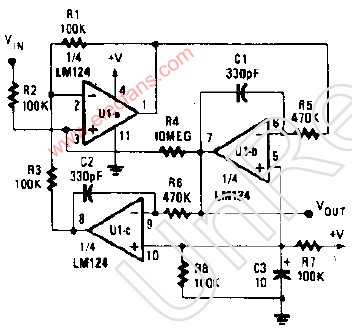 
有源RC低通濾波器
圖中所示
2009-09-16 16:40:063253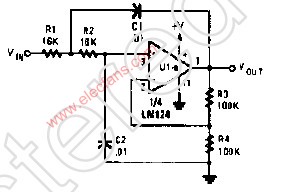 
有源高通濾波器
2009-09-16 16:24:532585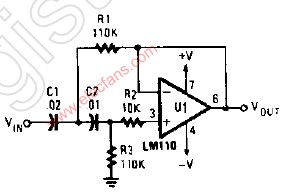 
RC有源濾波器實驗實驗目的1. 熟悉有源濾波器構成及其特性；2. 學會測量有源濾波器幅頻特性。；儀器及設備1. 示波器；2. 信號發生器。；
2009-05-15 00:32:328519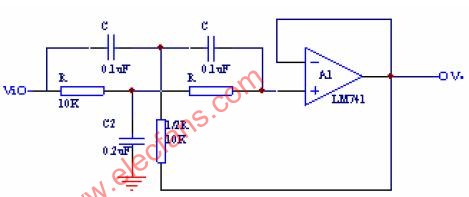 
二階RC濾波器的傳遞函數表
2009-05-08 08:53:5511611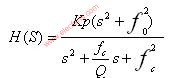 
在霍爾傳惑器的信號調理電路中應用RC有源高通濾波器和RC無源低通濾波器．
2009-04-07 14:40:2654
雙二次型RC有源帶通濾波器電路圖
2009-03-30 09:33:151680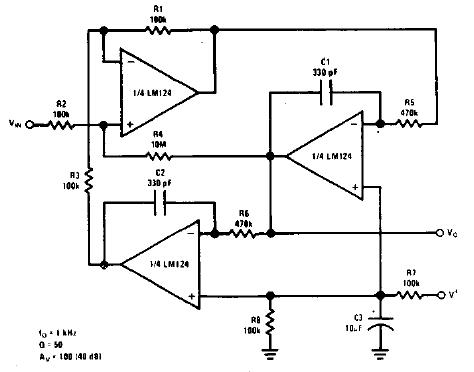 
高通濾波器電路圖
2009-03-30 09:19:027122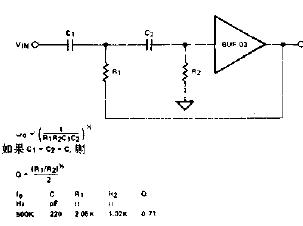 
高通濾波器設計內容有：高通濾波器的基本電路和方程，二階高通勃脫華斯濾波器，四階高通濾波器，二階高通濾波器的設計步驟提要，四階高通濾波器的設計步驟提要。
2008-12-01 12:42:5493 RC有源濾波器的快速設計:掌握低通、高通、帶通、帶阻等最基本的二階RC有源濾波器的快速設計方法與性能參數的測試技術。
重點：二階RC有源濾波器的快速設計方法。難
2008-12-01 08:23:01331 RC微分電路
輸出信號與輸入信號的微分成正比的電路，稱為微分電路。
原理：從圖一得：
2008-01-17 12:28:3751127 
正在加载...
電子發燒友App
工商網監
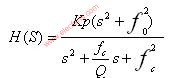
評論