針對數字匹配濾波器（DMF）的FPGA實現提出一種優化結構。利用16位移位寄存器（SRL16E）的存儲潛力，設計遞歸延遲線（RDL）;再利用RDL抽頭個數倍減而抽頭樣本速率倍增的特點和時分復用技術，提出DMF的遞歸折疊結構。該結構以提高工作時鐘頻率為代價，增大延遲線的采樣率以及相關運算單元的吞吐率，從而成倍降低DMF的資源消耗。當采用l/4遞歸折疊結構時，資源消耗僅為優化前的l/3.

　　隨著直接序列擴頻（DSSS）通信技術和軟件無線電技術的發展，全數字擴頻接收機成為研究的熱點。數字匹配濾波器（DMF）是全數字擴頻接收機的核心部件，它主要用于偽碼（PN）快速捕獲和解擴。傳統的DMF設計效率較低，當PN碼碼長較長時，需要占用較多的FPGA資源，成本較高。作者通過改進延遲線的結構，并結合時分復用技術，提出DMF的遞歸折疊結構，該結構極大地降低了DMF的資源消耗。

　　1 DMF的基本結構和參數

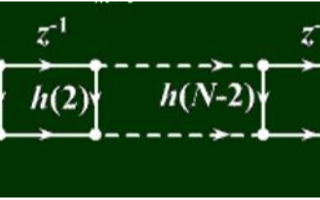
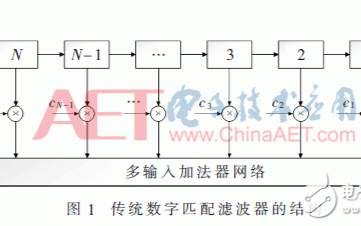
　　DMF是一種抽頭間隔即碼片周期為Tc、抽頭系數為擴頻序列（取值為±1）的特殊的FIR濾波器。其直接型結構由延遲線和相關運算單元（CCU）構成，如圖1所示.

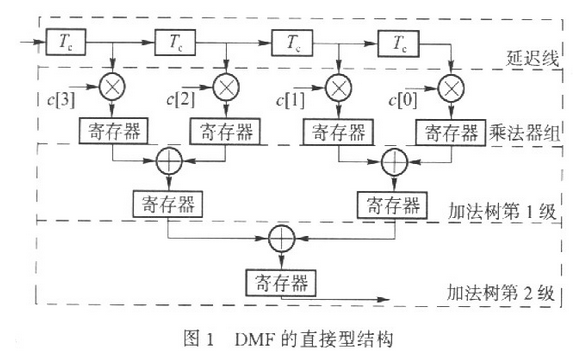
　　延遲線用于保存相關時間范圍（LTc）內的所有輸入樣本，它由L個延遲單元組成。雖然級聯多個D觸發器是實現延遲單元的最簡方法，但它將大量使用D觸發器，因此不宜用于構建量化位數大、階數高的DMF延遲線.FPGA擁有豐富的查找表（LUT）資源，它可以用16位循環移位寄存器（SRL16E）實現 l～16個節拍的信號延遲。對于M bit量化、過采樣倍數R≤16的DMF來說，構造一個延遲單元需要M個SRL16E.

　　如圖1所示，相關運算單元由L個乘法器和一個倒金字塔形的加法樹組成。加法樹的第1級有L/2個（M+1）bit二輸入同步加法器（參與運算的是延遲抽頭樣本，字長為M bit，為了防止計算溢出，在相加之前需要進行1 bit的符號位擴展）、第2級有L/2個（M+2）bit二輸入同步加法器，……，整個加法樹有L- 1個二輸入同步加法器。

　　DMF的量化位數、輸入采樣率以及工作頻率是影響DMF性能的3個關鍵參數，后兩個參數是優化結構的基礎，需要仔細權衡。

　　DMF的輸入為數字下變頻器的輸出（數字解調方案）或者模擬基帶ADC的輸出（模擬解調方案），其量化位數一般都為8 bit以上.DMF的資源消耗近似正比于量化位數，因此需要在這兩者之間做出適當的折衷。文獻中給出了DMF的量化精度對解擴性能的影響及DMF量化位數的選擇依據。一般認為高斯信道下DMF選擇3 bit量化較為合適，此時量化誤差造成的性能損失不大，再增加量化位數并不能明顯改善系統性能。為了敘述的一般性，定義DMF的輸入量化位數為M.

　　采樣率是全數字接收機的關鍵參數之一，為了降低實現難度，避免采樣率變換環節，DMF的采樣率一般為接收機中頻或基帶ADC的采樣率。為了降低對ADC前端模擬濾波器性能的要求并提高PN碼同步精度，需要提高采樣率。然而采樣率的提高將增加接收機的運算量，從而導致占用更多的FP-GA資源，因此同樣需要折衷考慮。工程上采樣率一般是chip速率的整數倍，用過采樣倍數R表示，R值一般取4～8.

　　模塊的數據處理能力與其并行程度（取決于硬件規模）和吞吐率（取決于工作頻率）成正比。在額定數據處理能力下，提高模塊的工作頻率可以降低對模塊并行程度的要求，即工作頻率和設計規模是可以互換的。目前主流的高端FPGA的工作頻率可以達到200～400 MHz，遠遠高于DMF的采樣率，采用時分復用方式將大大降低硬件資源消耗量。

　　作者提出的遞歸折疊型DMF，充分利用SRL16E的存儲潛力，用遞歸結構降低延遲線的資源消耗，然后利用遞歸延遲線具有抽頭個數倍減而抽頭樣本速率倍增的特點來時分復用相關運算單元，從而降低乘法器和加法器的數量。上述措施可成倍降低DMF消耗的硬件資源。

　　2 遞歸延遲線的結構與特點

　　傳統的延遲單元用SRL16E實現R（R≤16）位移位寄存，在每個采樣周期Ts內，延遲單元中的R個樣本全部右移一位，這樣，輸入樣本經過R×Ts后送到抽頭處，從而實現了Tc時延.R位移位操作未能充分利用SRL16E的存儲潛力，為此作者提出遞歸延遲線結構。在該結構中，無論R取何值，SRL16E 都進行16位移位操作。這樣保存L×R個輸入樣本總共需要M×L×R/16個SRL16E，僅為傳統結構的R/16.下面結合圖2進行時序分析.

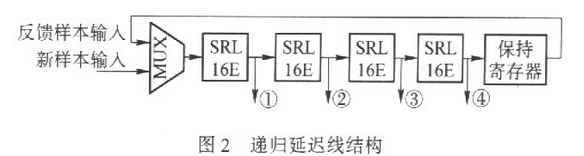
　　由于SRL16E進行16位移位操作，為了保證其時延等于Tc，移位周期必須為Tc/16.把R×Ts/16定為延遲線的工作時鐘周期，那么工作時鐘頻率為chip速率的16倍，即采樣率的C倍，其中C△16/R，因此每C個工作時鐘周期才輸入一個新樣本。不妨假設新樣本在第nC個工作時鐘周期（后面簡稱為時刻）到來，其中n為整數。如果時刻m是C的整數倍，MUX把新樣本推入延遲線，否則MUX把保持寄存器中的舊樣本反饋到延遲線的輸入端。

　　在nC時刻被MUX推入到延遲線入口的樣本，在經過L×R個時鐘周期后將在nC+L，×R時刻被推到保持寄存器中，然后在nC十L×R+l時刻（因為該時刻不是C的整數倍）將再次被送入到延遲線的入口，……;當該樣本第C次進入保持寄存器后，已是C（L×R+n+1）時刻，此時.MUX將選入一個新的樣本，而它將被拋棄。這樣一個新樣本在遞歸延遲線中剛好循環C次，歷時C（L×R+1）時鐘周期，從而實現了L×Tc+Ts時間的延遲。

　　下面分析遞歸延遲線各抽頭的輸出樣本在時間上的相位關系。設nC時刻輸入樣本為x（n），那么抽頭①～④處的輸出樣本應該是x（n- R），x（n2R），x（n-3R）和x（n-4R）;nC+1時刻延遲線輸入的應該是已經延遲L×R+1時鐘周期的樣本，即x（n-L×R/C）;抽頭 ①～④處的輸出樣本應該是x（n-R- L×R/C），x（n-2R-L×R/C），x（n- 3R-L×R/C）和x（n-4R-L×R/C）;第nC+c（0≤c≤C-1）時刻延遲線輸入的應該是已經延遲c（LR+1）時鐘周期的樣本，即 x（n-c×L×R/C）。那么抽頭①～④處的輸出樣本應該是x（n-R-c×L×R/C），x（n-2R-c×L×R/C），x（n-3R- c×L×R/C）和x（n-4R-c×L×R/C）。

　　可以看出，同一個抽頭在相鄰2個時刻輸出的樣本相差L×R/C個采樣點，即1/C個碼周期。這樣遞歸延遲線把一個碼周期內的信號樣本分解到C個相位上，并在C個時鐘周期內依次串行輸出，從而以多相的方式實現了信號延遲的功能。

　　遞歸延遲線僅需L/C個延遲單元即可實現L×Tc時延，它以工作時鐘頻率提高C倍為代價，將資源消耗量壓縮到優化前的1/C.例如，當R=4時，C=16/R=4，即資源消耗僅為原先的25%.

　　3 遞歸折疊DMF

　　3.1 遞歸折疊DMF的結構

　　遞歸延遲線不僅使抽頭數減少到優化前的1/C，而且使抽頭的樣本輸出速率增大C倍。與之對應，相關運算單元中乘法器和加法器的個數分別從L和L-1減少到 L/C和L/C-1，同時工作頻率提高C倍。在C個工作時鐘周期內，相關運算單元根據遞歸延遲線分解的信號相位，依次計算出C個相位上的接收信號與PN序列的部分相關值，并利用累加器完成部分相關值的合并，從而得到完整的相關值。根據這個思路，作者提出遞歸折疊結構的DMF如圖3所示。

　　該結構在遞歸延遲線的基礎上，折疊使用相關運算單元，從而用一個L/C抽頭的DMF完成L階匹配濾波運算。

　　圖3是一個1/2遞歸折疊濾波器，其參數為：L=8，R=8，C=2用1個4抽頭DMF時分復用實現了8階匹配濾波。時序分析與上節相似。不失一般性，假設在偶時刻輸入新樣本，那么在第0，2，4，6，…時刻MUX將輸入樣本推入延遲線，在第1，3，5，7，…時刻，MUX將保持寄存器中的樣本反饋到延遲線的入口。經過一段時間后，某個抽頭在偶時刻的樣本與其在下一時刻輸出的樣本在相位上將相差半個碼相位周期，因此在相鄰的時鐘周期內，加載到各抽頭的乘法系數也相差半個碼相位周期。累加器合并奇、偶時刻的部分相關結果，從而得到完整的結果.

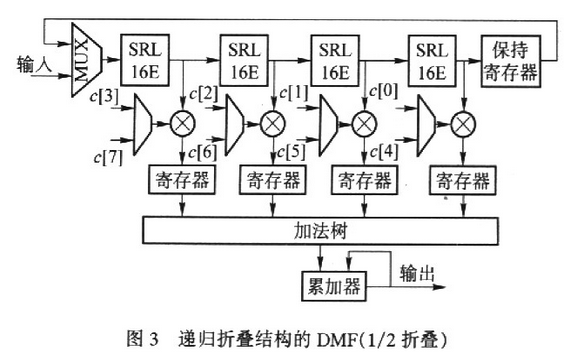
　　圖4為l/4遞歸折疊濾波器的結構框圖。（參數為L=8，R=4，C=4）。時序更加復雜，在相鄰時鐘周期內，抽頭樣本之間的相位差為1/4碼周期.

　　3.2 遞歸折疊DMF與傳統DMF資源消耗對比

　　為了評估優化效果，表1給出了采用基本結構和改進的折疊結構實現DMF所消耗的資源（L=256，M=4，R=4，采樣率為fs）.

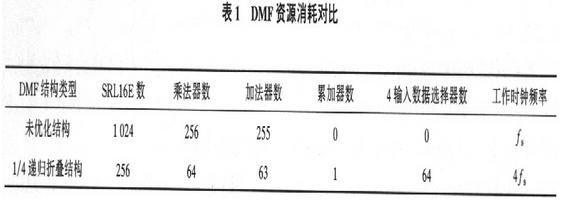
　　從表1可以看出，除了需要1個額外的累加器以及L/C個C輸入數據選擇器之外，遞歸折疊DMF所消耗的資源（包括SRLL6E、乘法器和加法器）壓縮到接近未優化結構的l/C，但是其工作時鐘頻率也提高到原來的C倍，這也證明了硬件規模和工作頻率可以互換。

　　然而工作時鐘頻率的提高是有限制的，更高的工作頻率要求采用檔次更高的FPGA或者需要在FPGA的細節實現中付出更高的代價，因此在設計遞歸折疊DMF 時，需要統籌考慮chip速率、過采樣倍數和FPGA的工作時鐘頻率。例如。對于xilinx Virtex2系列FPGA，當chip速率不超過10 MHz/s時，可以選用1/4或者l/2遞歸折疊結構，此時工作頻率不超過160 MHz，時序要求適中。

　　4 結束語

　　利用工作時鐘頻率與設計規模可互換的原理，通過遞歸延遲線、折疊相關運算單元以及時分復用技術，使遞歸折疊結構大大降低了DMF的資源消耗。該結構已經應用于某型號中頻數字化直接序列擴頻接收機中，應用結果表明優化效果明顯。在采樣率為40.96 MHz，工作時鐘頻率為163.84 MHz的條件下，通過4倍時分復用，其資源消耗約為優化前的l/3.