【導語】時間序列是指以固定時間為間隔的序列值。本篇教程將教大家用 Python 對時間序列進行特征分析。

1、什么是時間序列？

時間序列是指以固定時間為間隔的、由所觀察的值組成的序列。根據觀測值的不同頻率，可將時間序列分成小時、天、星期、月份、季度和年等時間形式的序列。有時候，你也可以將秒鐘和分鐘作為時間序列的間隔，如每分鐘的點擊次數和訪客數等等。

為什么我們要對時間序列進行分析呢？

因為當你想對一個序列進行預測時，首先要完成分析這個步驟。除此之外，時間序列的預測也具有極大商業價值，如企業的供求量、網站的訪客量以及股票價格等，都是極其重要的時間序列數據。

那么，時間序列分析都包括哪些內容呢？

要做好時間序列分析，必須要理解序列的內在屬性，這樣才能做出更有意義且精準的預測。

2、如何在 Python 中引入時間序列？

關于時間序列的數據大都存儲在 csv 文件或其他形式的表格文件里，且都包含兩個列：日期和觀測值。

首先我們來看 panda 包里面的 read_csv() 函數，它可以將時間序列數據集（關于澳大利亞藥物銷售的 csv 文件）讀取為 pandas 數據框。增加一個 parse_dates=['date'] 字段，可以把包含日期的數據列解析為日期字段。

from dateutil.parser import parse import matplotlib as mplimport matplotlib.pyplot as pltimport seaborn as snsimport numpy as npimport pandas as pdplt.rcParams.update({'figure.figsize': (10, 7), 'figure.dpi': 120})# Import as Dataframedf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])df.head()

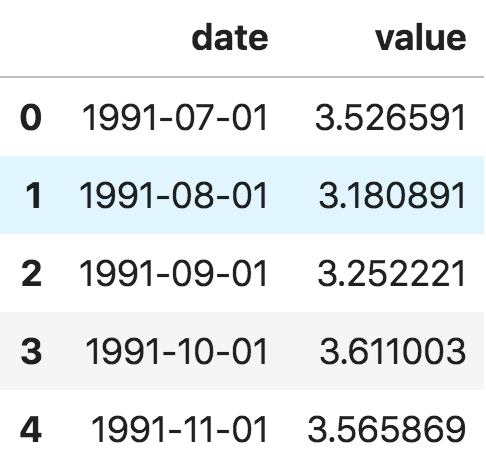
時間序列數據框

此外，你也可以將文件讀取為 pandas 序列，把日期作為索引列，只需在 pd.read_csv() 中指定 index_col 參數。

ser = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')ser.head()

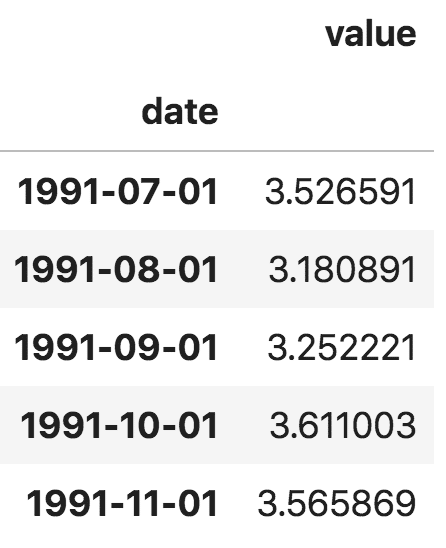
pandas 序列

注意，在 pandas 序列中，'value' 列的位置高于 'date' 列，這表明它是一個 pandas 序列而非數據框。

3、什么是面板數據？

面板數據同樣是基于時間的數據集。

不同之處是，除了時間序列，面板數據還包括一個或多個相關變量，這些變量也是在同個時間段內測得的。

面板數據中的列包括有助于預測 y 值的解釋變量，這些特征列可用于之后的預測。以下是關于面板數據的例子：

# dataset source: https://github.com/rouseguydf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/MarketArrivals.csv')df = df.loc[df.market=='MUMBAI', :]df.head()

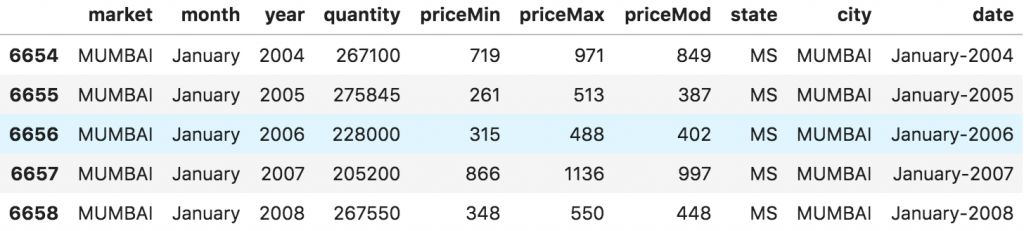
面板數據

4、時間序列可視化

接下來，我們用 matplotlib 對序列進行可視化。

# Time series data source: fpp pacakge in R.import matplotlib.pyplot as pltdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')#DrawPlotdef plot_df(df, x, y, title="", xlabel='Date', ylabel='Value', dpi=100): plt.figure(figsize=(16,5), dpi=dpi) plt.plot(x, y, color='tab:red') plt.gca().set(title=title, xlabel=xlabel, ylabel=ylabel)plt.show()plot_df(df,x=df.index,y=df.value,title='Monthlyanti-diabeticdrugsalesinAustraliafrom1992to2008.')

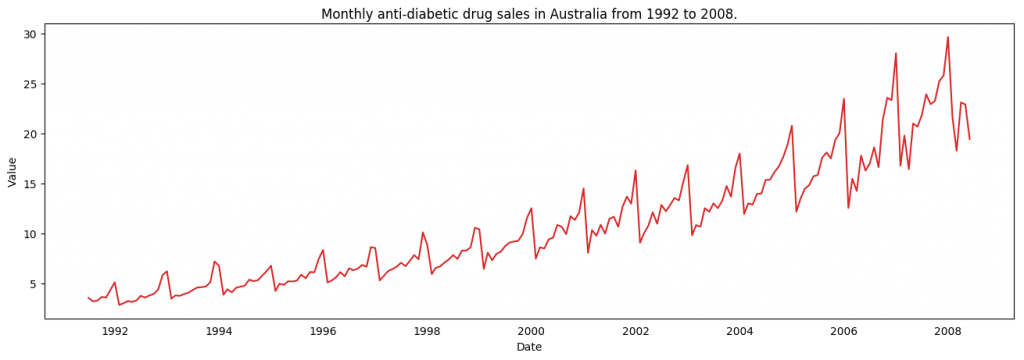
時間序列可視化

由于所有的值都為正數，無論使用 y 軸的哪一側都可以看到增長的趨勢。

# Import datadf = pd.read_csv('datasets/AirPassengers.csv', parse_dates=['date'])x = df['date'].valuesy1 = df['value'].values# Plotfig, ax = plt.subplots(1, 1, figsize=(16,5), dpi= 120)plt.fill_between(x, y1=y1, y2=-y1, alpha=0.5, linewidth=2, color='seagreen')plt.ylim(-800, 800)plt.title('Air Passengers (Two Side View)', fontsize=16)plt.hlines(y=0, xmin=np.min(df.date), xmax=np.max(df.date), linewidth=.5)plt.show()

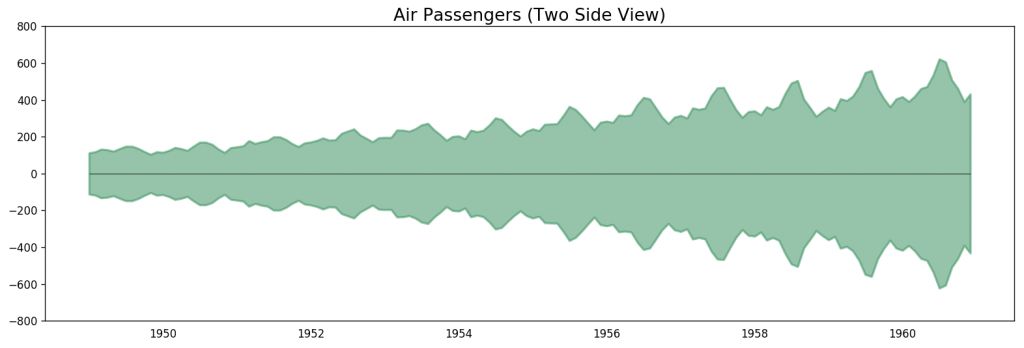
飛機乘客數據 - 雙邊序列

由于這是一個月份的時間序列，每年的走勢都遵循著特定重復的模式，你可以在同一個圖中畫出單獨每年的折線。這樣有助于對這幾年的趨勢走向進行平行對比。

季節性時間序列的可視化：

#ImportDatadf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')df.reset_index(inplace=True)# Prepare datadf['year'] = [d.year for d in df.date]df['month'] = [d.strftime('%b') for d in df.date]years = df['year'].unique()# Prep Colorsnp.random.seed(100)mycolors = np.random.choice(list(mpl.colors.XKCD_COLORS.keys()), len(years), replace=False)# Draw Plotplt.figure(figsize=(16,12), dpi= 80)for i, y in enumerate(years): if i > 0: plt.plot('month', 'value', data=df.loc[df.year==y, :], color=mycolors[i], label=y) plt.text(df.loc[df.year==y, :].shape[0]-.9, df.loc[df.year==y, 'value'][-1:].values[0], y, fontsize=12, color=mycolors[i])# Decorationplt.gca().set(xlim=(-0.3, 11), ylim=(2, 30), ylabel='$Drug Sales$', xlabel='$Month$')plt.yticks(fontsize=12, alpha=.7)plt.title("Seasonal Plot of Drug Sales Time Series", fontsize=20)plt.sho

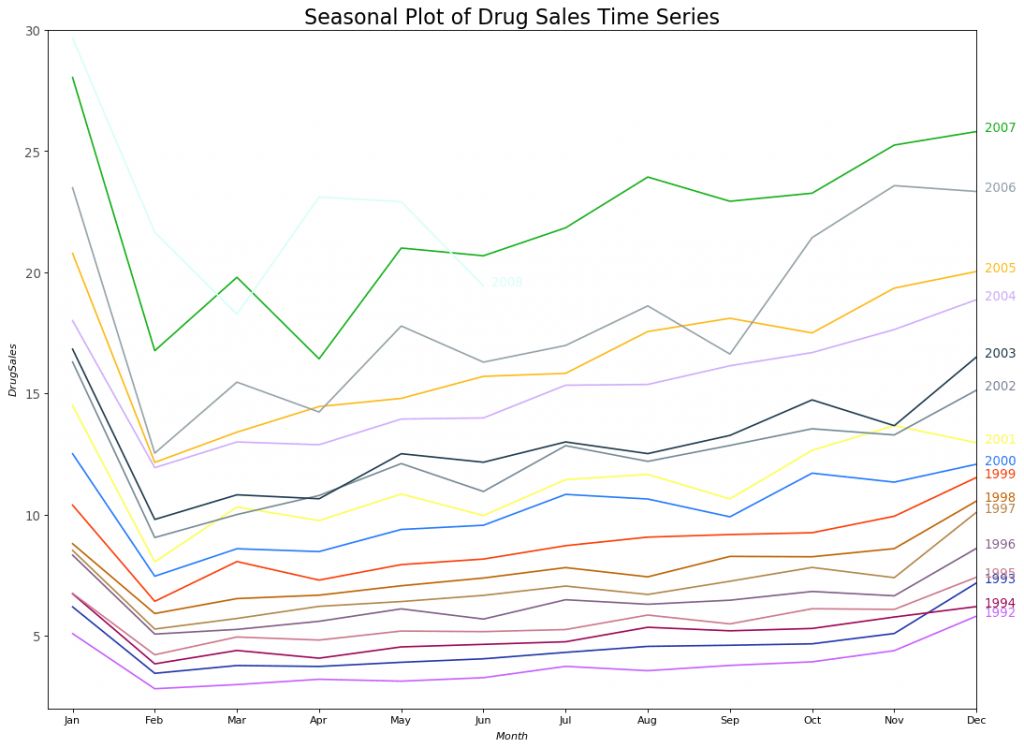
藥品銷售的季節性時間序列圖

每年的二月份，藥品銷售會有一次大幅度下跌，三月份會回漲，四月份再次下跌，以此規律循環。很明顯，該模式以年為單位，每年循環往復。

不過，隨著年份的變化，藥品銷售總體呈上升趨勢。你可以選擇使用箱型圖將這一趨勢進行可視化，可以方便看出每一年的變化。同樣地，你也可以按月份繪制箱型圖，來觀察每個月的變化。

按月份（季節）和年份繪制箱型圖：你可以將數據處理成以季節為時間間隔，然后觀察特定年份內值的分布，也可以將全部時間的數據進行對比。

# Import Datadf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')df.reset_index(inplace=True)# Prepare datadf['year'] = [d.year for d in df.date]df['month'] = [d.strftime('%b') for d in df.date]years = df['year'].unique()# Draw Plotfig, axes = plt.subplots(1, 2, figsize=(20,7), dpi= 80)sns.boxplot(x='year', y='value', data=df, ax=axes[0])sns.boxplot(x='month', y='value', data=df.loc[~df.year.isin([1991, 2008]), :])# Set Titleaxes[0].set_title('Year-wise Box Plot\n(The Trend)', fontsize=18);axes[1].set_title('Month-wise Box Plot\n(The Seasonality)', fontsize=18)plt.show

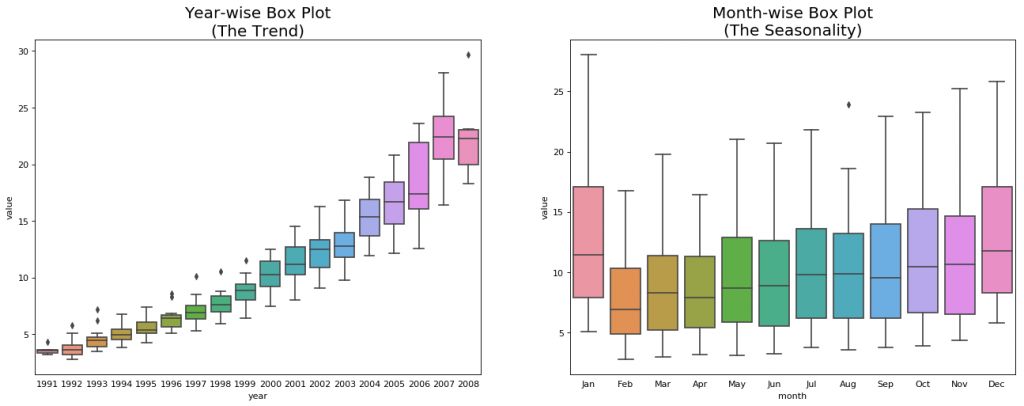
年份序列和月份序列的箱型圖

上面的箱型圖可以使年份和月份的序列更易于觀察。同樣，在月份的箱線圖中，十二月和一月的藥品銷售額明顯更高，這是因為處于假期折扣季。

到目前為止，我們了解了通過相似性來觀察時間序列的模式，接下來，如何發現這些常見模式中的差異呢？

5、時間序列的模式

任何一個時間序列都可以被分解成以下幾個部分：基準 + 趨勢成分 + 季節成分 + 殘差成分。

趨勢是指時間序列中上升或下降的傾斜程度。但季節成分是由于受季節因素影響而產生的周期性模式循環，也可能受每年內不同月份、每月內不同日期、工作日或周末，甚至每天內不同時間的影響。

然而，不一定所有的時間序列都具備趨勢或季節性。一個時間序列也可能不存在趨勢，但具有季節性。反之亦然。

因此，一個時間序列可以被想象成趨勢、季節性和殘差項的組合。

fig, axes = plt.subplots(1,3, figsize=(20,4), dpi=100)pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/guinearice.csv', parse_dates=['date'], index_col='date').plot(title='Trend Only', legend=False, ax=axes[0])pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv', parse_dates=['date'], index_col='date').plot(title='Seasonality Only', legend=False, ax=axes[1])pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/AirPassengers.csv',parse_dates=['date'],index_col='date').plot(title='TrendandSeasonality',legend=False,ax=axes[2]

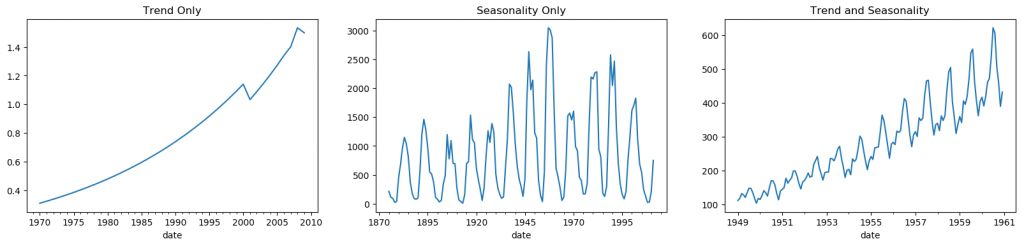
時間序列的模式

另一個需要考慮的方面是周期性模式。當序列中的上升和下降，不是按日歷中的特定時間間隔發生時，就會出現這種情況。注意不要把“周期”作用和“季節”作用混淆。

那么，如何區分“周期”和“季節”呢？

如果序列中的模式不是以日歷中特定間隔循環出現的，那么就是周期。因為與季節性不同，周期作用通常受到商業或社會經濟等因素的影響。

6、加法與乘法時間序列

根據趨勢和季節的固有屬性，一個時間序列可以被建模為加法模型或乘法模型，也就是說，序列中的值可以用各個成分的加和或乘積來表示：

加法時間序列：

值 = 基準 + 趨勢 + 季節 + 殘差

乘法時間序列：

值 = 基準 x 趨勢 x 季節 x 殘差

7、如何將時間序列的成分分解出來？

通過將一個時間序列視為基準、趨勢、季節指數及殘差的加法或乘法組合，你可以對時間序列進行經典分解。

statsmodels 的 seasonal_decompose 函數可以使這一過程非常容易。from statsmodels.tsa.seasonal import seasonal_decomposefrom dateutil.parser import parse# Import Datadf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')# Multiplicative Decompositionresult_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')# Additive Decompositionresult_add = seasonal_decompose(df['value'], model='additive', extrapolate_trend='freq')# Plotplt.rcParams.update({'figure.figsize': (10,10)})result_mul.plot().suptitle('Multiplicative Decompose', fontsize=22)result_add.plot().suptitle('Additive Decompose', fontsize=22)plt.sho

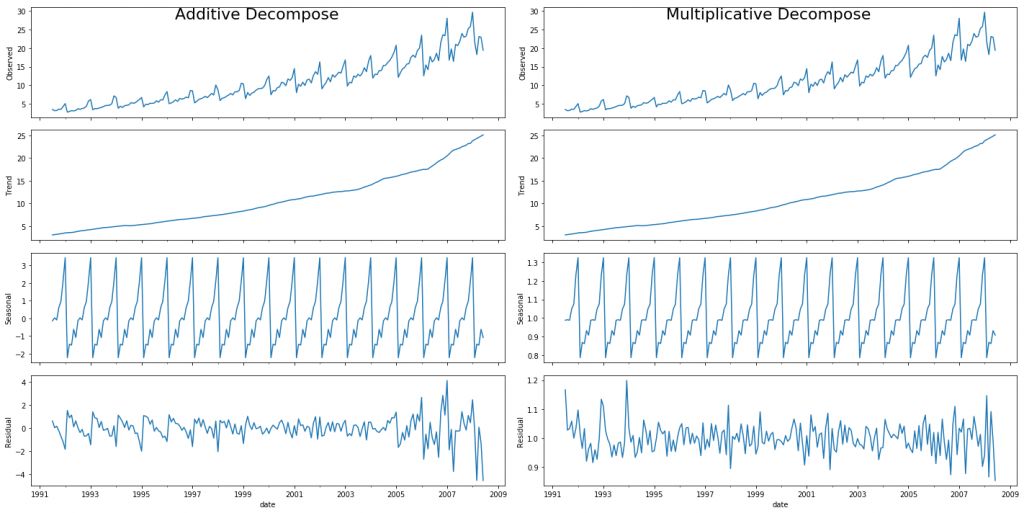
加法和乘法分解

設置 extrapolate_trend='freq' 有助于處理序列首部趨勢和殘差中的空值。

如果你仔細觀察加法分解中的殘差項，會發現其中仍保留了一些模式。然而，乘法分解中的殘差項看起來更具有隨機性。因此，對于這一特定序列來說，采用乘法分解更合適。

趨勢、季節和殘差成分的數值輸出均存儲在 result_mul 里，下面我們對其進行提取，并放入數據框中：

# Extract the Components ----# Actual Values = Product of (Seasonal * Trend * Resid)df_reconstructed = pd.concat([result_mul.seasonal, result_mul.trend, result_mul.resid, result_mul.observed], axis=1)df_reconstructed.columns = ['seas', 'trend', 'resid', 'actual_values']df_reconstructed.head()

仔細觀察，會發現 seas、trend 和 resid 三列的乘積正好等于 actual_values。

8、平穩和非平穩時間序列

平穩是時間序列的屬性之一。平穩序列中的值不是時間的函數。

也就是說，平穩序列的平均值、方差和自相關性等統計特征始終為常數。序列的自相關性是指該序列與之前的值間的相關性。

平穩的時間序列也不包括季節因素的影響。那么如何分辨一個序列是否平穩呢？讓我們來看幾個例子：

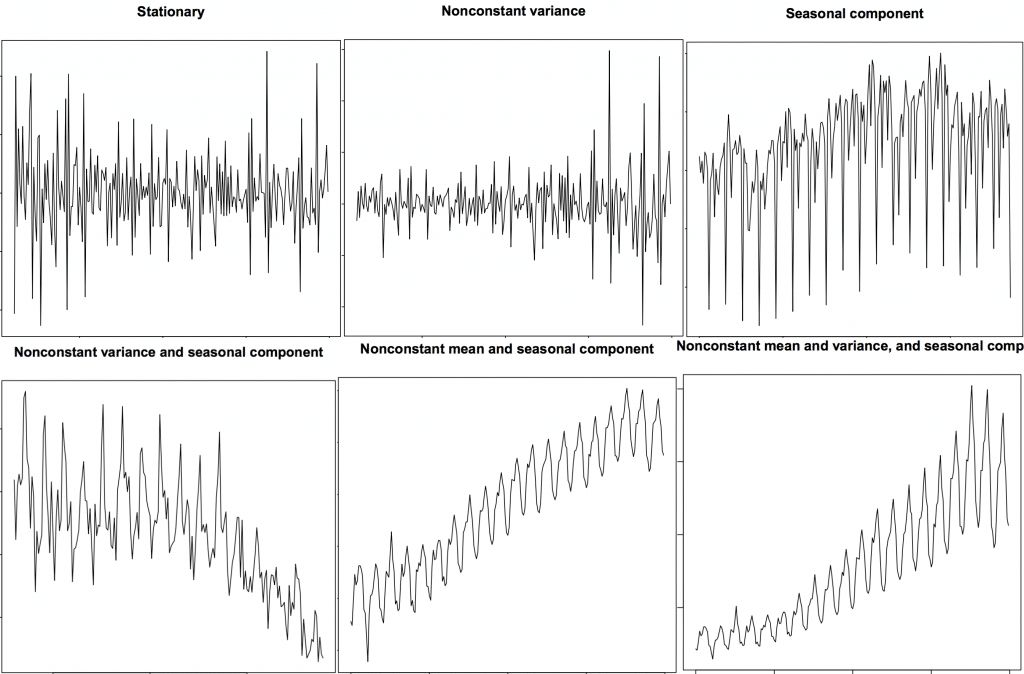
平穩和非平穩時間序列

上圖來自 R 語言的 TSTutorial 教程。

為什么說序列平穩很重要呢？

我會對此稍微做一些解釋，但要清楚一點，通過采用合適的變換，我們近乎可以將任何時間序列變得平穩。大多數統計預測方法最初都是為平穩時間序列而設計的。預測過程的第一步是通過一些變換，來將非平穩序列變成平穩序列。

9、如何將時間序列變平穩？

你可以通過以下幾種方式得到平穩序列：

求序列的差分

求序列的 log 值

求序列的 n 次方根

把上面三種方法相結合

將時間序列平穩化最普遍且便捷的方法是對序列進行差分運算，至少執行一次，直到序列趨于平穩。

那么什么是差分呢？

如果 Y_t 為時間 't' 對應的值，那么第一個差分值為 Y = Yt – Yt-1。簡單來說，對序列進行差分運算就是用下一個值減去當前值。如果第一次差分不能使序列平穩，你可以嘗試做第二次差分，直到符合要求。

舉個例子，有這樣一個序列：[1, 5, 2, 12, 20]

第一次差分運算的結果為：[5-1, 2-5, 12-2, 20-12] = [4, -3, 10, 8]

第二次差分運算的結果為：[-3-4, -10-3, 8-10] = [-7, -13, -2]

10、為什么要在預測前將非平穩序列變平穩？

對平穩序列進行預測要相對容易一些，預測結果也更可信。其中一個重要原因是，自回歸預測模型本質上是線性回歸模型，將序列自身的滯后作為預測因子。

如果預測因子之間互不相關，線性回歸的效果最優。那么將序列平穩化就可以解決這一問題，因為它可以去除任何持久的自相關性，所以可以使預測模型中的預測因子近乎獨立。

現在我們知道了使序列平穩化的重要性，那么應該如何檢查一個序列是否平穩呢？

11、如何測試平穩性？

我們可以像之前那樣，通過繪制序列圖來觀察一個序列是否平穩。

另一種方法是將序列分解成兩個或多個連續的部分，并求其統計值，如平均值、方差和自相關系數。如果這些統計值間的差異很大，那么該序列大概率不是平穩序列。

盡管如此，你仍需要一種方法來定量地判斷某個序列是否平穩。一個名為“單位根檢驗”的統計檢驗方法可以解決這一問題。

單位根檢驗有如下幾種方法：

ADF Test (Augmented Dickey Fuller test)

KPSS Test (Kwiatkowski-Phillips-Schmidt-Shin) — 趨勢平穩

PP Test (Philips Perron test)

最常用的方法是 ADF test，零假設為：用時間序列對單位根進行處理，結果是不平穩。如果 P 值小于顯著性水平 0.05，則拒絕零假設，即不成立。

另一方面，KPSS test 可用來檢測趨勢平穩性。零假設與 P 值含義都與 ADH test 相反。以下代碼基于 Python 的 statsmodels 包執行了兩種檢測方法：

from statsmodels.tsa.stattools import adfuller, kpssdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])# ADF Testresult = adfuller(df.value.values, autolag='AIC')print(f'ADF Statistic: {result[0]}')print(f'p-value: {result[1]}')for key, value in result[4].items(): print('Critial Values:') print(f' {key}, {value}')# KPSS Testresult = kpss(df.value.values, regression='c')print('\nKPSS Statistic: %f' % result[0])print('p-value: %f' % result[1])for key, value in result[3].items(): print('Critial Values:') print(f' {key}, {value}'

from statsmodels.tsa.stattools import adfuller, kpssdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])# ADF Testresult = adfuller(df.value.values, autolag='AIC')print(f'ADF Statistic: {result[0]}')print(f'p-value: {result[1]}')for key, value in result[4].items(): print('Critial Values:') print(f' {key}, {value}')# KPSS Testresult = kpss(df.value.values, regression='c')print('\nKPSS Statistic: %f' % result[0])print('p-value: %f' % result[1])for key, value in result[3].items(): print('Critial Values:') print(f' {key}, {value}'

12、白噪聲與平穩序列的差別是什么？

和平穩序列一樣，白噪聲也是關于時間的函數，它的均值和方差始終不變。但區別在于，白噪聲是完全隨機的，且均值為零。

白噪聲沒有任何模式。如果你把調頻廣播的聲波訊號想象成時間序列，調頻道時的空白聲音就是白噪聲。

從數學上來講，一個完全隨機且均值為零的序列就是白噪聲。

randvals = np.random.randn(1000)pd.Series(randvals).plot(title='RandomWhiteNoise',color='k')

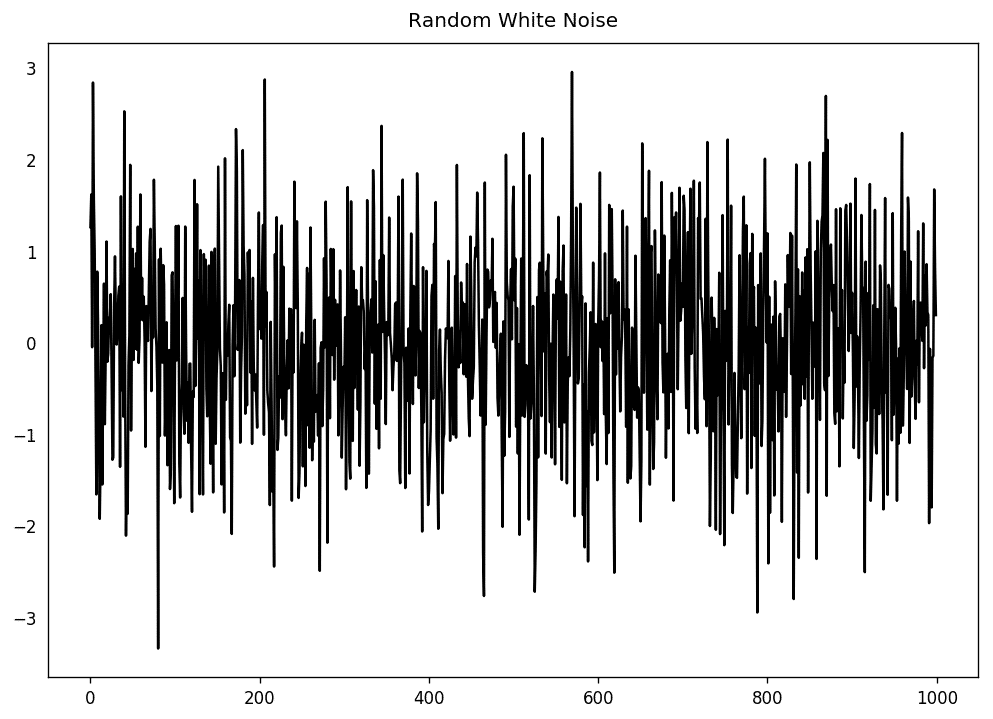
隨機白噪聲

13、如何對時間序列去趨勢？

對時間序列去趨勢，是指去除序列中的趨勢成分。但要如何提取趨勢成分呢？有以下幾種方法：

減去與時間序列擬合程度最好的曲線。這條最優曲線可由線性回歸模型獲得，時間步長作為預測因子。如需處理更復雜的趨勢，你可以嘗試在模型中使用二次項 (x^2)。

減去由時間序列分解得到的趨勢成分。

減去均值。

使用過濾器，如 Baxter-King (statsmodels.tsa.filters.bkfilter) 或 Hodrick-Prescott (statsmodels.tsa.filters.hpfilter)，來去除移動平均趨勢線或周期性成分。

下面我們來執行這兩種方法：

# Using scipy: Subtract the line of best fitfrom scipy import signaldf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])detrended = signal.detrend(df.value.values)plt.plot(detrended)plt.title('DrugSalesdetrendedbysubtractingtheleastsquaresfit',fontsize=16)

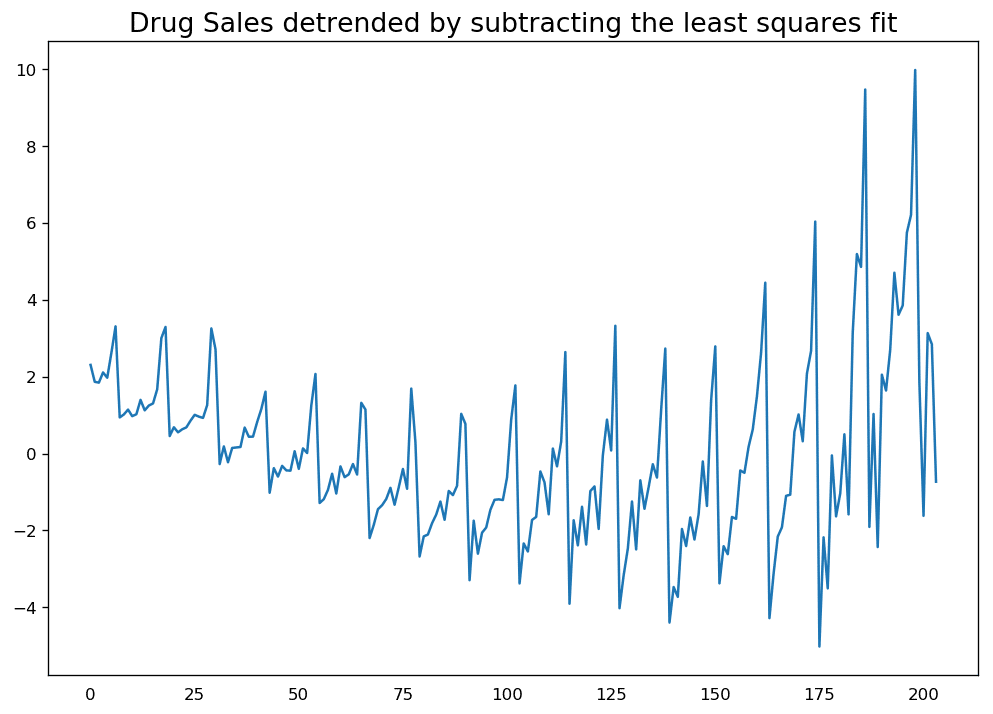
通過減掉最小二乘擬合線對時間序列去趨勢

# Using statmodels: Subtracting the Trend Component.from statsmodels.tsa.seasonal import seasonal_decomposedf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')detrended = df.value.values - result_mul.trendplt.plot(detrended)plt.title('Drug Sales detrended by subtracting the trend component', fontsize=16)

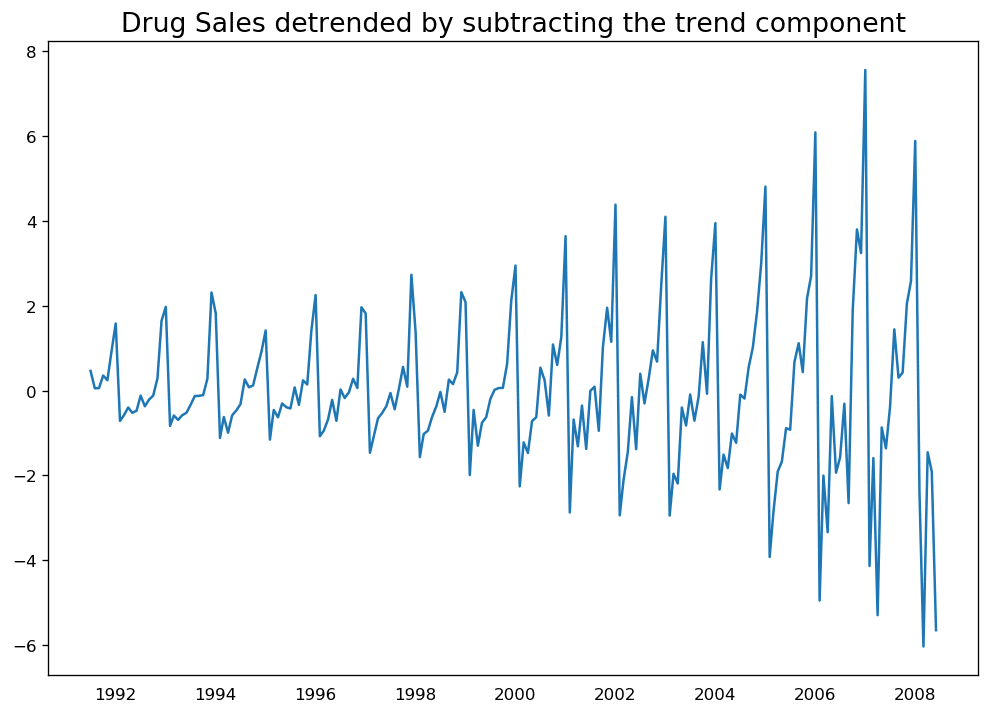
通過減掉趨勢成分對時間序列去趨勢

14、如何對時間序列去季節性？

對時間序列去季節性同樣有多種方法，如下：

把特定長度的移動平均值作為季節窗口。

對序列做季節性差分（用當前值減去上個季度的值）。

用當前序列除以由 STL 分解得到的季節指數。

若除以季節指數的效果不好，可以嘗試取序列的對數，然后對其去季節。之后你可以通過指數運算來恢復原來的值。

# Subtracting the Trend Component.df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')# Time Series Decompositionresult_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')# Deseasonalizedeseasonalized = df.value.values / result_mul.seasonal# Plotplt.plot(deseasonalized)plt.title('Drug Sales Deseasonalized', fontsize=16)plt.plot

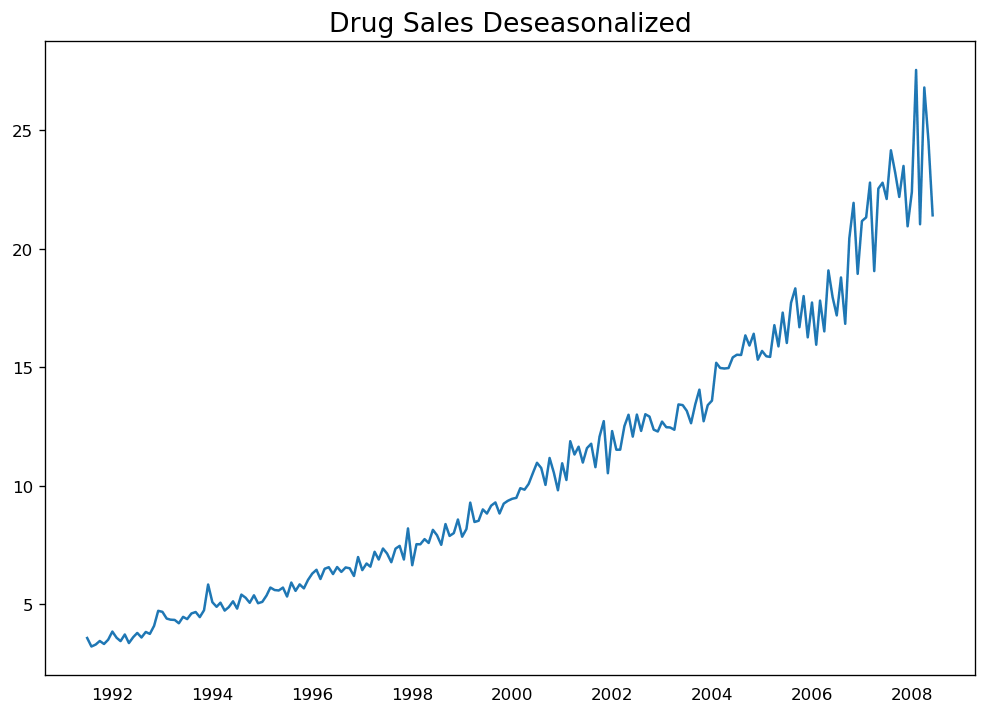
對時間序列去季節

15、如何檢測時間序列的季節性？

一般方法是畫出序列圖，觀察固定的時間間隔是否有重復模式出現。因此，季節性的類型由時鐘或日歷決定：

一天中的小時

月份中的日期

星期

月份

年份

不過，如果你想對季節性做一個明確的檢驗，可以使用自相關函數 (ACF) 圖，接下來的部分會做相關詳細介紹。當季節模式明顯時，ACF 圖中季節窗口的整數倍處會反復出現特定的尖峰。

例如，藥品銷售的時間序列是月份序列，每年會出現重復的模式，你會在第 12、24、36 個序列值處看到尖峰。

必須要提醒你的是，現實生活中的數據集很少會出現特別明顯的模式，可能會被一些噪聲污染，所以需要更加仔細觀察其中的模式。

from pandas.plotting import autocorrelation_plotdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')# Draw Plotplt.rcParams.update({'figure.figsize':(9,5), 'figure.dpi':120})autocorrelation_plot(df.value.tolist())

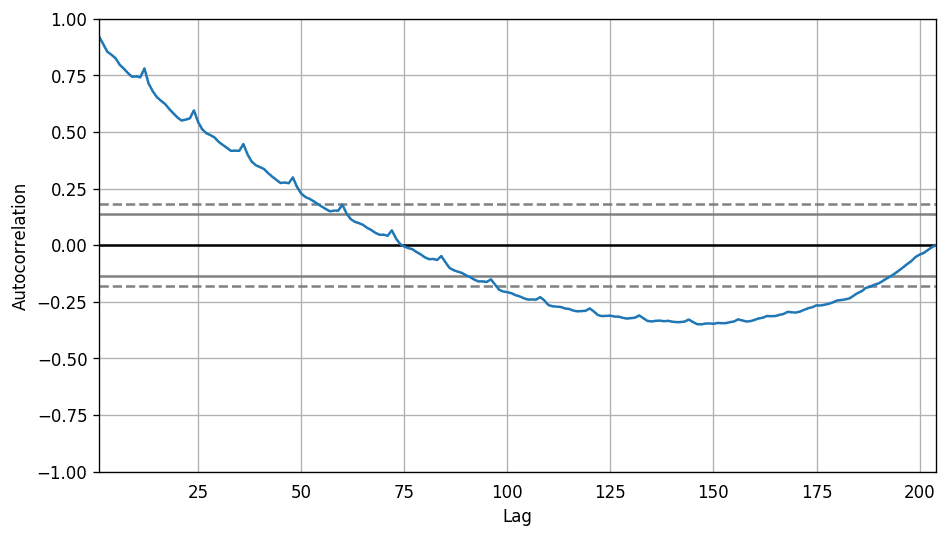
自相關系數圖

16、如果處理時間序列中的缺失值？

有時候，時間序列中會出現缺失的值或日期。這意味著，某些數據沒有獲取到，或者無法對這些時間段進行觀測。也可能那些時間的測量值本身為零，這種情況下你只需對其填充零。

第二種情況，你不應該直接用序列的均值對缺失處進行填充，尤其當該序列不是平穩序列時。比較暴力但有效的解決方法是用前一個值來填充缺失處。

根據序列的內在屬性，你可以嘗試多種方法。以下是幾種比較有效的填充方法：

向后填充法

線性插值法

二次插值法

最近鄰均值法

季節均值法

為了評估缺失值的填充效果，我在時間序列中手動加入缺失值，用以上幾種方法對其進行填充，然后計算填充后的序列與原序列的均方誤差。

# # Generate datasetfrom scipy.interpolate import interp1dfrom sklearn.metrics import mean_squared_errordf_orig = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date').head(100)df = pd.read_csv('datasets/a10_missings.csv', parse_dates=['date'], index_col='date')fig, axes = plt.subplots(7, 1, sharex=True, figsize=(10, 12))plt.rcParams.update({'xtick.bottom' : False})## 1. Actual -------------------------------df_orig.plot(title='Actual', ax=axes[0], label='Actual', color='red', style=".-")df.plot(title='Actual', ax=axes[0], label='Actual', color='green', style=".-")axes[0].legend(["Missing Data", "Available Data"])## 2. Forward Fill --------------------------df_ffill = df.ffill()error = np.round(mean_squared_error(df_orig['value'], df_ffill['value']), 2)df_ffill['value'].plot(title='Forward Fill (MSE: ' + str(error) +")", ax=axes[1], label='Forward Fill', style=".-")## 3. Backward Fill -------------------------df_bfill = df.bfill()error = np.round(mean_squared_error(df_orig['value'], df_bfill['value']), 2)df_bfill['value'].plot(title="Backward Fill (MSE: " + str(error) +")", ax=axes[2], label='Back Fill', color='firebrick', style=".-")## 4. Linear Interpolation ------------------df['rownum'] = np.arange(df.shape[0])df_nona = df.dropna(subset = ['value'])f = interp1d(df_nona['rownum'], df_nona['value'])df['linear_fill'] = f(df['rownum'])error = np.round(mean_squared_error(df_orig['value'], df['linear_fill']), 2)df['linear_fill'].plot(title="Linear Fill (MSE: " + str(error) +")", ax=axes[3], label='Cubic Fill', color='brown', style=".-")## 5. Cubic Interpolation --------------------f2 = interp1d(df_nona['rownum'], df_nona['value'], kind='cubic')df['cubic_fill'] = f2(df['rownum'])error = np.round(mean_squared_error(df_orig['value'], df['cubic_fill']), 2)df['cubic_fill'].plot(title="Cubic Fill (MSE: " + str(error) +")", ax=axes[4], label='Cubic Fill', color='red', style=".-")# Interpolation References:# https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html# https://docs.scipy.org/doc/scipy/reference/interpolate.html## 6. Mean of 'n' Nearest Past Neighbors ------def knn_mean(ts, n): out = np.copy(ts) for i, val in enumerate(ts): if np.isnan(val): n_by_2 = np.ceil(n/2) lower = np.max([0, int(i-n_by_2)]) upper = np.min([len(ts)+1, int(i+n_by_2)]) ts_near = np.concatenate([ts[lower:i], ts[i:upper]]) out[i] = np.nanmean(ts_near) return outdf['knn_mean'] = knn_mean(df.value.values, 8)error = np.round(mean_squared_error(df_orig['value'], df['knn_mean']), 2)df['knn_mean'].plot(title="KNN Mean (MSE: " + str(error) +")", ax=axes[5], label='KNN Mean', color='tomato', alpha=0.5, style=".-")## 7. Seasonal Mean ----------------------------def seasonal_mean(ts, n, lr=0.7): """ Compute the mean of corresponding seasonal periods ts: 1D array-like of the time series n: Seasonal window length of the time series """ out = np.copy(ts) for i, val in enumerate(ts): if np.isnan(val): ts_seas = ts[i-1::-n] # previous seasons only if np.isnan(np.nanmean(ts_seas)): ts_seas = np.concatenate([ts[i-1::-n], ts[i::n]]) # previous and forward out[i] = np.nanmean(ts_seas) * lr return outdf['seasonal_mean'] = seasonal_mean(df.value, n=12, lr=1.25)error = np.round(mean_squared_error(df_orig['value'], df['seasonal_mean']), 2)df['seasonal_mean'].plot(title="Seasonal Mean (MSE: " + str(error) +")", ax=axes[6], label='Seasonal Mean', color='blue', alpha=0.5, s

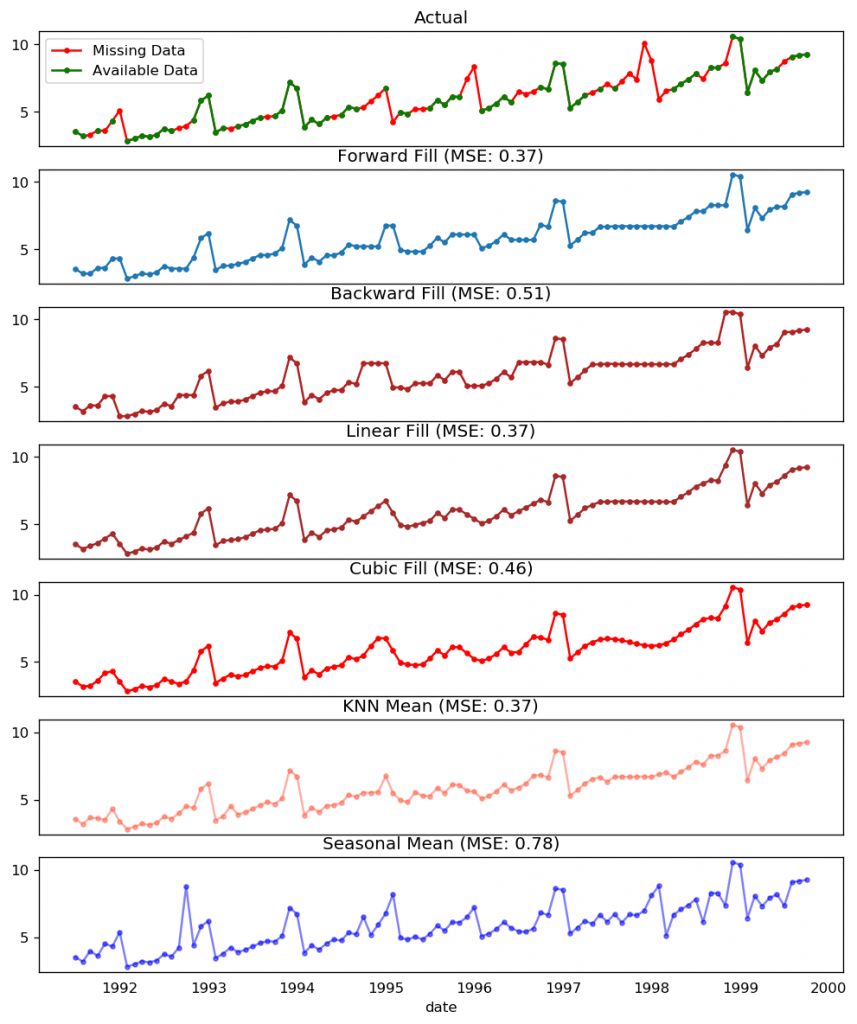
缺失值處理

17、什么是自相關和偏自相關函數？

簡單來說，自相關就是一個序列的值與自己本身具有相關性。如果一個序列呈現顯著自相關，意味著序列的前一個值可用于預測當前值。

偏自相關也傳達了類似的信息，但更偏重于序列與自身滯后序列的相關性，消除了由于較短滯后所導致的任何相關性。

from statsmodels.tsa.stattools import acf, pacffrom statsmodels.graphics.tsaplots import plot_acf, plot_pacfdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')# Calculate ACF and PACF upto 50 lags# acf_50 = acf(df.value, nlags=50)# pacf_50 = pacf(df.value, nlags=50)# Draw Plotfig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100)plot_acf(df.value.tolist(), lags=50, ax=axes[0])plot_pacf(df.value.tolist(),lags=50,ax=axes[1

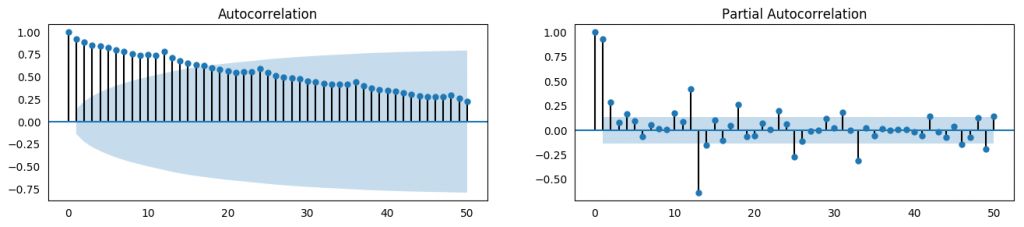
ACF 和 PACF

18、如何計算偏自相關系數？

序列滯后 k 處的偏自相關系數是 Y 的自回歸方程的滯后系數。Y 的自回歸方程是指 Y 以自己的滯后作為預測因子的線性回歸。

舉個例子，如果 Y_t 為當前序列，Y_t-1 即為滯后期為 1 的 Y 值，那么滯后期為 3 處 (Y_t-3) 的偏自相關系數是下面方程中的 α3：

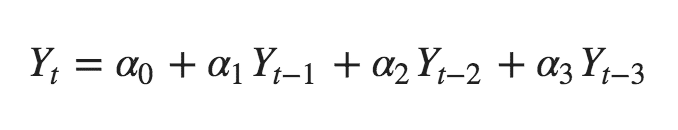
自回歸方程

19、滯后圖

滯后圖是時間序列與自身滯后的分布圖，通常用來檢驗自相關性。如果序列中出現下圖中的模式，那么說明該序列具有自相關性。如果沒有出現這些模型，該序列很可能為隨機白噪聲。

在下面太陽黑子區的例子中，隨著滯后期的增長，圖中的點越來越分散。

from pandas.plotting import lag_plotplt.rcParams.update({'ytick.left' : False, 'axes.titlepad':10})# Importss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')# Plotfig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)for i, ax in enumerate(axes.flatten()[:4]): lag_plot(ss.value, lag=i+1, ax=ax, c='firebrick') ax.set_title('Lag ' + str(i+1))fig.suptitle('Lag Plots of Sun Spots Area \n(Points get wide and scattered with increasing lag -> lesser correlation)\n', y=1.15)fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)for i, ax in enumerate(axes.flatten()[:4]): lag_plot(a10.value, lag=i+1, ax=ax, c='firebrick') ax.set_title('Lag ' + str(i+1))fig.suptitle('Lag Plots of Drug Sales', y=1.05)plt.sh

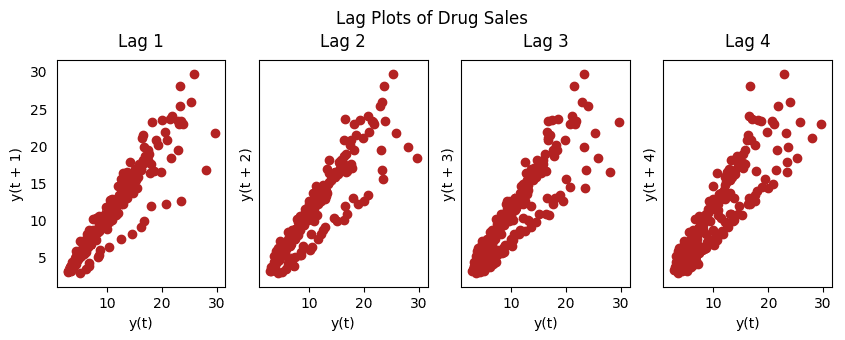
藥品銷售滯后圖

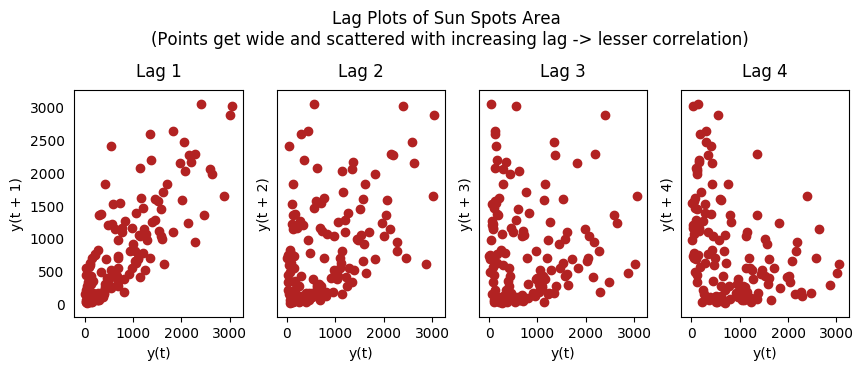
太陽黑子滯后圖

20、如何評估時間序列的可預測性？

一個時間序列的模式越有規律，就越容易預測。可以用近似熵來量化時間序列的規律性和波動的不可預測性。

近似熵越高，意味著預測難度越大。

另一個選擇是樣本熵。

樣本熵與近似熵類似，但在不同的復雜度上更具有一致性，即使是小型時間序列。例如，相比于“有規律”的時間序列，一個數據點較少的隨機時間序列的近似熵較低，但一個較長的隨機時間序列卻有較高的近似熵。

因此，樣本熵更適于解決該問題。

# https://en.wikipedia.org/wiki/Approximate_entropyss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')rand_small = np.random.randint(0, 100, size=36)rand_big = np.random.randint(0, 100, size=136)def ApEn(U, m, r): """Compute Aproximate entropy""" def _maxdist(x_i, x_j): return max([abs(ua - va) for ua, va in zip(x_i, x_j)]) def _phi(m): x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)] C = [len([1 for x_j in x if _maxdist(x_i, x_j) <= r]) / (N - m + 1.0) for x_i in x] return (N - m + 1.0)**(-1) * sum(np.log(C)) N = len(U) return abs(_phi(m+1) - _phi(m))print(ApEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.651print(ApEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.537print(ApEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 0.143print(ApEn(rand_big,?m=2,?r=0.2*np.std(rand_big)))?????#?0.?

0.65147049703335340.53747752249734890.08983769407988440.7369242960384561

# https://en.wikipedia.org/wiki/Sample_entropydef SampEn(U, m, r): """Compute Sample entropy""" def _maxdist(x_i, x_j): return max([abs(ua - va) for ua, va in zip(x_i, x_j)]) def _phi(m): x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)] C = [len([1 for j in range(len(x)) if i != j and _maxdist(x[i], x[j]) <= r]) for i in range(len(x))] return sum(C) N = len(U) return -np.log(_phi(m+1) / _phi(m))print(SampEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.78print(SampEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.41print(SampEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 1.79print(SampEn(rand_big, m=2, r=0.2*np.std(rand_big))) # 2.

0.78533113663800390.41887013457621214inf2.181224235989778del sys.path[0]

21、為什么要對時間序列做平滑處理？如果操作？

對時間序列做平滑處理有以下幾個用處：

減少噪聲影響，從而得到過濾掉噪聲的、更加真實的序列。

平滑處理后的序列可用作特征，更好地解釋序列本身。

可以更好地觀察序列本身的趨勢。

那么如果進行平滑處理呢？現討論以下幾種方法：

取移動平均線

做 LOESS 平滑（局部回歸）

做 LOWESS 平滑（局部加權回歸）

移動平均是指對一個滾動的窗口計算其平均值，該窗口的寬度固定不變。但你必須謹慎選擇窗口寬度，因為窗口過寬會導致序列平滑過度。例如，如果窗口寬度等于季節長度，就會消除掉季節因素的作用。

LOESS 是 LOcalized regrESSion 的縮寫，該方法會在每個點的局部近鄰點做多次回歸擬合。此處可以使用 statsmodels 包，你可以使用參數 frac 控制平滑程度，即決定周圍多少個點參與回歸模型的擬合。

from statsmodels.nonparametric.smoothers_lowess import lowessplt.rcParams.update({'xtick.bottom' : False, 'axes.titlepad':5})# Importdf_orig = pd.read_csv('datasets/elecequip.csv', parse_dates=['date'], index_col='date')# 1. Moving Averagedf_ma = df_orig.value.rolling(3, center=True, closed='both').mean()# 2. Loess Smoothing (5% and 15%)df_loess_5 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.05)[:, 1], index=df_orig.index, columns=['value'])df_loess_15 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.15)[:, 1], index=df_orig.index, columns=['value'])# Plotfig, axes = plt.subplots(4,1, figsize=(7, 7), sharex=True, dpi=120)df_orig['value'].plot(ax=axes[0], color='k', title='Original Series')df_loess_5['value'].plot(ax=axes[1], title='Loess Smoothed 5%')df_loess_15['value'].plot(ax=axes[2], title='Loess Smoothed 15%')df_ma.plot(ax=axes[3], title='Moving Average (3)')fig.suptitle('How to Smoothen a Time Series', y=0.95, fontsize=14)plt.sho

時間序列的平滑處理

22、如何用格蘭杰因果關系檢驗判斷一個時間序列是否可以預測另一個？

格蘭杰因果關系檢驗可用作檢測一個時間序列是否可以用來預測另一個序列。那么格蘭杰因果關系檢驗是如何進行運算的呢？

該檢驗基于一個假設，即 X 導致了 Y 的發生，那么基于 Y 的先前值與 X 的先前值得到的 Y 的預測值，要優于僅根據 Y 本身得到的預測值。

statsmodels 包提供了便捷的檢驗方法。它可以接受一個二維數組，其中第一列為值，第二列為預測因子。

零假設為：第二列的序列與第一列不存在格蘭杰因果關系。如果 P 值小于顯著性水平 0.05，就可以拒絕零假設，從而知道 X 的滯后是起作用的。

第二個參數 maxlag 表示該檢驗中涉及了 Y 的多少個滯后期。

from statsmodels.tsa.stattools import grangercausalitytestsdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])df['month'] = df.date.dt.monthgrangercausalitytests(df[['value','month']],maxlag=2)

Granger Causalitynumber of lags (no zero) 1ssr based F test: F=54.7797 , p=0.0000 , df_denom=200, df_num=1ssr based chi2 test: chi2=55.6014 , p=0.0000 , df=1likelihood ratio test: chi2=49.1426 , p=0.0000 , df=1parameter F test: F=54.7797 , p=0.0000 , df_denom=200, df_num=1Granger Causalitynumber of lags (no zero) 2ssr based F test: F=162.6989, p=0.0000 , df_denom=197, df_num=2ssr based chi2 test: chi2=333.6567, p=0.0000 , df=2likelihood ratio test: chi2=196.9956, p=0.0000 , df=2parameterFtest:F=162.6989,p=0.0000,df_denom=197,df_num=2

在上面的例子中，全部測試結果中的 P 值都為零，說明 'month' 可用作預測航班的乘客數量。