近日,研究人員利用基于神經網絡的新算法,成功模擬了量子系統的“穩態”。利用神經網絡估計并模擬波函數和密度矩陣,大大降低了計算復雜度和算力需求,為解決量子科學和信息領域的幾個突出問題打下了基礎。
即使是在日常生活中,大自然也受到量子物理定律的支配。這些定律解釋了生活中的常見現象,如光、聲、熱,甚至是臺球桌上球的運動軌跡。這些日常都是符合大眾視覺和想象的,我們都已經習以為常。但是當涉及到大量相互作用的粒子時,量子物理定律所解釋的現象,大部分和我們的直覺相違背。
為了研究由大量粒子組成的量子系統,物理學家必須首先能夠模擬這類系統。解釋量子系統內部運行機制的方程可以由超級計算機解出,但是,雖然摩爾定律預測,計算機的處理能力每兩年翻一番,但這與解決量子物理面臨的挑戰所需的計算能力相去甚遠。
造成這個困難的原因是,預測量子系統的本質是非常復雜的,要想跟上量子系統規模的增長,計算力需要呈指數增長。這是一項“本質上極其復雜”的任務。EPFL納米系統理論物理實驗室負責人Vincenzo Savona教授表示。
“對于開放式量子系統,情況會變得更加復雜,因為系統會受到周圍環境的干擾,”薩沃納補充道。非常需要有效模擬開放量子系統的工具,因為量子科學和技術的大多數現代實驗平臺都是開放系統,物理學家一直在尋找新的方法來對這些系統模擬和測試。
近日,洛桑聯邦理工學院(EPFL)的研究人員采用神經網絡模擬量子系統的新計算方法,已經取得了重大進展。相關研究成果已在“物理評論快報”的三篇論文中發表。
論文摘要:
對開放量子系統性質的模擬,是解決量子科學和信息領域的幾個突出問題的前提。這個問題的難度在于系統的密度矩陣會隨著系統規模的增大呈指數級增長。本文提出一種變分方法,利用變分蒙特卡羅方法和密度矩陣的神經網絡,有效模擬了馬爾可夫開放量子系統的非平衡穩態。
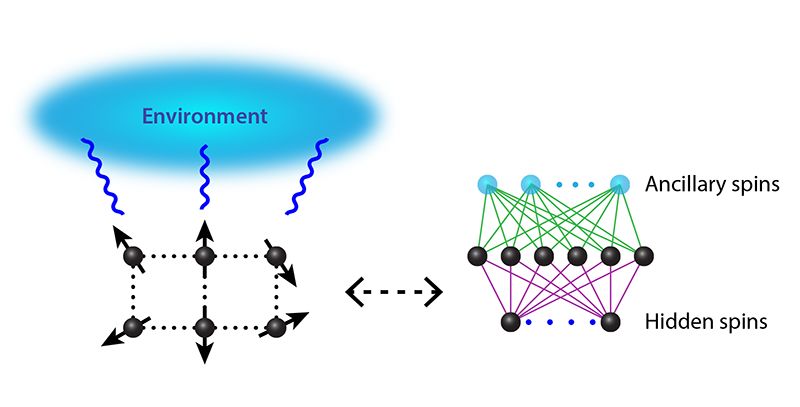
利用神經網絡(右)找到“開放”量子系統的靜止穩態(左)
在開放量子系統中,研究人員的目標是找到“穩態”,即不隨時間變化的量子態。確定這種狀態的形式理論已經存在。當系統包含多個量子粒子時,計算上可能會出現困難。要描述整個自旋系統,必須確定2^N種可能的狀態。僅僅存儲20次旋轉的這些信息需要大約8千兆字節的RAM,并且每增加一次旋轉,所需算力就會翻倍。在開放系統中處理相同數量的旋轉甚至更難,因為旋轉必須用“密度矩陣”ρ來描述。這個矩陣規模極大,元素數量為2^N×2^N個。
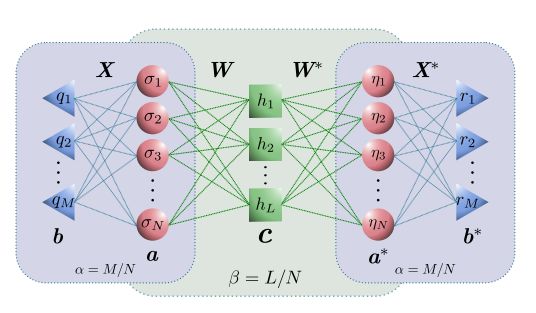
神經網絡ansatz對量子系統密度矩陣的圖形表示
神經網絡的優勢在于,它可以用很少的信息來近似模擬波函數或密度矩陣。神經網絡就像一個數學“盒子”,將一串數字(矢量或張量)作為輸入,并輸出另一個字符串。對于模擬N量子系統的特定任務,神經網絡函數可以作為波函數的“猜測”,將N個對象的狀態作為輸入。然后,研究人員讓網絡從實際或模擬數據進行“學習”,或將波函數決定的物理量進行最小化,來優化函數參數。一旦獲得了正確的猜測,就可用于計算其他物理屬性,其參數數量遠遠少于2^N 。
“這個研究基本上就是將神經網絡和機器學習的進步,與量子蒙特卡羅工具結合起來,”Savona說,他說的“量子蒙特卡羅工具”指的是物理學家用來研究復雜量子系統的大型算法工具包。科學家訓練了一個神經網絡來同時表示多個量子系統,可以通過其環境的影響投射的許多量子態。
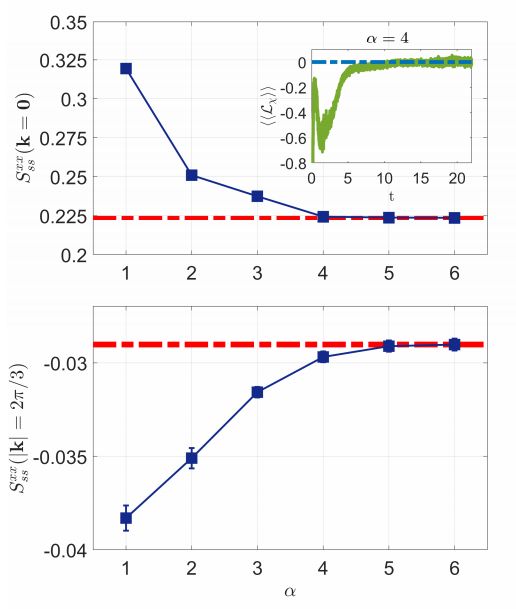
穩態自旋結構因子作為α=β的函數計算為3×3點陣,k = 0(上圖)和k =(2π/ 3,0)(下圖)
這一基于神經網絡的方法能夠讓物理學家預測相當大小的量子系統的性質。“這種新算法解決了開放式量子系統的問題,具有多功能性和擴展的潛力,”薩沃納說。該方法將成為研究復雜量子系統的首選工具,而且未來可以產生更多工具,比如評估噪聲干擾對量子硬件系統的影響。
-
神經網絡
+關注
關注
42文章
4789瀏覽量
101901 -
算法
+關注
關注
23文章
4660瀏覽量
94046 -
量子系統
+關注
關注
0文章
22瀏覽量
2676
原文標題:算法巨大突破!AI神經網絡能模擬量子系統了
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦


















評論