對神經網絡而言，使用同一架構的網絡，從不同初始值開始優(yōu)化，最終的泛化效果可以完全不同。在傳統(tǒng)的機器學習中，對優(yōu)化算法和泛化性能的研究是分開的，但對深度學習這樣的非凸問題而言，兩者是密不可分的。本文試圖對這個問題做出統(tǒng)一的解釋。

神經網絡有很多異于傳統(tǒng)機器學習系統(tǒng)（比如決策樹和SVM）的奇特性質。比如說過參化（over-parameterization）時并不會產生過擬合，而只會讓測試集上效果變好（泛化能力變好），如果用正好的參數去擬合數據，泛化能力反而變差。比如說有隱式正則化（implicit regularization）的能力，即同樣大小的模型，可以完全擬合正常數據，也可以完全擬合隨機數據，并且在完全擬合正常數據時自動具有泛化能力。

近日，F(xiàn)acebook人工智能研究院研究員，卡內基梅隆大學機器人系博士田淵棟團隊發(fā)表新作，試圖對這類傳統(tǒng)機器學習難以解釋的問題做出統(tǒng)一的理論解釋。

在本文預印本發(fā)布后，田淵棟博士本人在知乎上題為《求道之人，不問寒暑（三）》的專欄文章中，對這篇論文的思想脈絡和實現(xiàn)過程做出了精彩的解讀，并和讀者進行了深入討論。

經作者授權，新智元全文轉載如下：

神經網絡有很多異于傳統(tǒng)機器學習系統(tǒng)（比如決策樹和SVM）的奇特性質。比如說過參化（over-parameterization）時并不會產生過擬合，而只會讓測試集上效果變好（泛化能力變好），如果用正好的參數去擬合數據，泛化能力反而變差；比如說它有隱式正則化（implicit regularization）的能力，即同樣大小的模型，可以完全擬合正常數據，也可以完全擬合隨機數據，并且在完全擬合正常數據時自動具有泛化能力。

這些現(xiàn)象在傳統(tǒng)機器學習理論中不太能夠得到解釋，按照傳統(tǒng)理論，用大小恰好的模型去擬合數據集是最優(yōu)的，更小的模型，其復雜度不夠從而無法擬合數據，更大的模型則會過擬合數據，降低其泛化能力，要使大模型有優(yōu)秀的泛化能力，需要使用正則化方法。按照傳統(tǒng)理論，如果一個模型大到能夠擬合復雜度更高的隨機數據，那它為什么不在正常數據上過擬合？如果一個模型能在正常數據上具有泛化能力，那它不應該能完全擬合隨機數據——在神經網絡上同時看到這兩個現(xiàn)象，是非常奇怪的。

最近ICLR19的最優(yōu)論文“The Lottery Ticket Hypothesis”（網絡權重的彩票現(xiàn)象）又增加了傳統(tǒng)理論難以解釋的部分——對神經網絡而言，使用同一架構的網絡，從不同初始值開始優(yōu)化，最終的泛化效果可以完全不同。 而權重初始值在傳統(tǒng)的泛化理論中沒有什么地位。因為傳統(tǒng)上“優(yōu)化算法”和“泛化性能”這兩件事情是完全分開的。做泛化性能的文章往往假設背后的優(yōu)化算法能拿到最優(yōu)解，而不考慮優(yōu)化的細節(jié)；而做優(yōu)化算法的文章只關心在訓練集上的權重到局部極小值的收斂速度，并不關心這個局部極小值在測試集上會有什么效果。如果模型空間有限或者模型的最優(yōu)參數可以由凸優(yōu)化得到，那這樣做理所當然；但對深度學習這樣的非凸問題而言，兩者是密不可分的。

這次我們做的這篇文章（arxiv.org/abs/1905.1340）試圖提出一個統(tǒng)一的理論來解釋這些現(xiàn)象，包括神經網絡參數多時效果更好，有動態(tài)適應不同數據集的能力，還能解釋從不同初始值出發(fā)，泛化能力完全不同的網絡彩票現(xiàn)象。我們提出的這個理論對這些問題都有比較好的直觀解釋，并且還有一個統(tǒng)一的數學框架來支撐。

其根本的方案，是將訓練時的優(yōu)化過程和泛化能力結合起來，從而去分析傳統(tǒng)方法分析不了的情況。

首先我們采用了教師-學生網絡（student-teacher）的框架，假設數據集的標注由一個隱藏的（多層）教師網絡（teacher network）生成，然后依據教師網絡的輸入輸出，用梯度下降法去優(yōu)化學生網絡（student network）。學生和教師網絡的層數相同，但因為over-parameterization，學生的每一層可以有比教師更多的輸出結點（神經元）。在這個框架下，我們證明了在一些情況下的權重復原定理，即學生網絡的權重可以收斂于教師網絡的對應權重，以及如何靠攏，并且分析了在over-parameterization的情況下學生網絡可能的行為。由這些定理，可以給出一些神經網絡奇特性質的解釋。

對于結構化的數據，其對應生成數據的教師網絡較小，過參化得到的學生網絡中的結點會優(yōu)先朝著教師網絡的結點收斂過去，并且初始時和教師網絡結點重合較大的學生結點（也即是“幸運神經元”，lucky weights/nodes）會收斂得更快，這樣就會產生“勝者全拿”的效應，最后每個教師結點可能只有幾個幸運學生結點對應。對于隨機數據，其對應的教師網絡比較大，學生結點會各自分散向不同的教師結點收斂。這就是為什么同樣大小的模型可以同時擬合兩者。并且因為勝者全拿的效應，學生傾向于用最少的結點去解釋教師，從而對結構數據仍然具有泛化能力。

從這些解釋出發(fā)，大家可能猜到了，“The Lottery Ticket Hypothesis”就是因為lucky nodes/weights的緣故：保留lucky nodes而去除其它不必要的結點，不會讓泛化效果變差；但若是只保留lucky nodes，并且重新初始化它們的權重，那相當于中彩者重買彩票，再中彩的概率就很小了。而過參化的目的就是讓更多的人去買彩票，這樣總會有幾個人中彩，最終神經網絡的效果，就由它們來保證了——那自然過參化程度越好，最后泛化效果越好。

另外，對過參化的初步分析表明，一方面lucky student weights可以收斂到對應的teacher weights，而大部分無關的student weights/nodes可能會收斂到任意的區(qū)域去——但這并不要緊，因為這些結點的上層權重會收斂到零，以減少它們對網絡輸出的影響。這就附帶解釋了為何神經網絡訓練后的解往往具有平坦極小值（Flat Minima）性質：對無關的學生結點而言，任意改變它們的權重，對網絡輸出都沒有太大影響。

具體細節(jié)是怎么做的呢？如果大家有興趣的話，可以繼續(xù)看下去。

雖然學生網絡接收到的信號只來自于教師的最終輸出層，對教師中間層如何輸出毫無知覺，但因為教師的前向傳遞和學生的反向傳遞算法，教師中間層和對應的學生中間層，這兩者其實是有隱含聯(lián)系的。這篇文章首先找到了一個學生網絡-教師網絡的一個很有趣的對應關系，即學生中間層收集到的梯度和對應教師層輸出的關系，然后借著這個對應關系，就可以找到學生網絡的權重和教師網絡的權重的對應關系。在此之上，再加一些基本假設，就可以有相應的權重復原定理。

這篇文章的基本假設很簡單，即教師同層兩個神經元同時被激活的概率遠遠小于各自單獨被激活的概率。這個假設相對來說是比較實際的：如果每個神經元只負責輸入信號的某個特性，那這些特性同時出現(xiàn)的概率相比單獨出現(xiàn)的概率要小很多。那么如何檢查這個假設呢？很簡單，按照這個假設，如果輸入是零均值分布，假設激活函數是ReLU，那神經元的bias就應當是負的，這樣它只對輸入的一小部分數據有正響應。事實似乎確實如此，我們在文章中檢查了VGG11/16這兩個在ImageNet上的預訓練網絡（都采用Conv-BN-ReLU架構）的BatchNorm層的bias，發(fā)現(xiàn)絕大部分都是負的，也就是說在訓練后網絡里的那些神經元確實每個負責不一樣的特性。

與之前平均場（Mean Field）的一系列文章相比，這篇文章不需要假設權重滿足獨立同分布這個非常嚴格且只在初始化時才成立的條件，可以用于分析網絡優(yōu)化的整個過程，事實上，我一直覺得多層神經網絡的優(yōu)化過程和平均場或者熱力學的箭頭是相反的：熱力學里系統(tǒng)從非平衡點到達平衡點的過程是抹消結構的過程，而神經網絡的優(yōu)化是從隨機初始的權重中創(chuàng)造并且強化結構的過程。這篇文章曾經打算投去年的ICML，原本的題目叫作“潘多拉的盒子”，也就是說，從隨機漲落的權重中，依著不同的數據集，可以收斂出任意的結構出來，但因為OpenGo的項目一直拖，一直到一年半以后才有比較初步的結果。

另一個附帶的結果是，從這篇文章的分析里可以比較清楚地看到“上層調制”這種機制的作用。很多人對多層神經網絡的疑問是：既然多層神經網絡號稱是對輸入特征進行不斷組合以獲得效果更好的高層特征，那為什么不可以采用自底向上的機制，每次單獨訓練一層，等訓練完再建上一層？依據這篇文章，回答是如果沒有上層的監(jiān)督信號，那底層的特征組合數量會指數級增長，并且生成的特征大多是對上層任務無用的。唯有優(yōu)化時不停聽取來自上層的信號，有針對性地進行組合，才可以以極高的效率獲得特定任務的重要特征。而對權重的隨機初始化，是賦予它們在優(yōu)化時滑向任意組合的能力。

原文鏈接：

https://zhuanlan.zhihu.com/p/67782029

以下是新智元對論文內容的簡編：

本文分析了深度ReLU網絡的訓練動態(tài)過程及其對泛化能力的影響。使用教師和學生的設置，我們發(fā)現(xiàn)隱藏學生節(jié)點接收的梯度，和深度ReLU網絡的教師節(jié)點激活之間存在新的關系。通過這種關系，我們證明了兩點：（1）權重初始化為接近教師節(jié)點的學生節(jié)點，會以更快的速度向教師節(jié)點收斂，（2）在過參數化的環(huán)境中，當一小部分幸運節(jié)點收斂到教師節(jié)點時，其他節(jié)點的fan-out權重收斂為零。

在本文中，我們提出了多層ReLU網絡的理論框架。該框架提供了對深度學習中的多種令人費解的現(xiàn)象的觀察，如過度參數化，隱式正則化，彩票問題等。

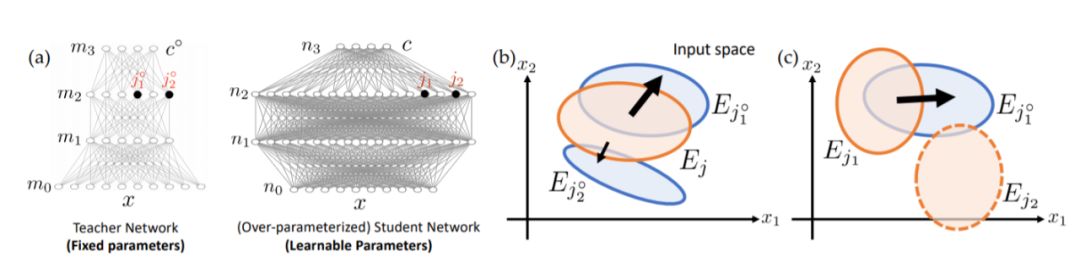
圖1

圖2

基于這個框架，我們試圖用統(tǒng)一的觀點來解釋這些令人費解的經驗現(xiàn)象。本文使用師生設置，其中給過度參數化的深度學生ReLU網絡的標簽，是具有相同深度和未知權重的固定教師ReLU網絡的輸出（圖1（a））。在這個角度來看，隱藏的學生節(jié)點將隨機初始化為不同的激活區(qū)域。（圖2（a））。

依托這個框架，本研究主要解決以下幾個問題：

擬合

結構化和隨機數據。在梯度下降動態(tài)下，一些學生節(jié)點恰好與教師節(jié)點重疊，將進入教師節(jié)點并覆蓋教師節(jié)點。不管對于中間節(jié)點數量較少的小型教師網絡的結構化數據，或者對具有中間節(jié)點數量較多的大型教師網絡的隨機數據，情況都是如此。這也解釋了為什么同一個網絡可以同時適應結構化和隨機數據（圖2（a-b））。

過參數化

在過度參數化中，許多學生節(jié)點在每一層進行隨機初始化。任何教師節(jié)點都更可能與某些學生節(jié)點有很大部分的重疊，這會導致快速收斂（圖2（a）和（c），）。這也解釋了為什么網絡容量恰好適合數據的訓練模型的性能表現(xiàn)會更差。

平滑極小值問題

深層網絡經常會收斂到“平滑極小值”。此外，雖然存在爭議，平滑極小值似乎意味著良好的泛化能力，而尖銳的極小值往往導致不良的泛化能力。

而在我們的理論中，在與結構化數據進行擬合時，只有少數幸運的學生節(jié)點收斂至教師節(jié)點，而對于其他節(jié)點，他們的fan-out權重縮小為零，使得它們與最終結果無關，產生平滑極小值，學生節(jié)點沿大多數維度上（“不幸節(jié)點”）的運動導致輸出變化最小。另一方面，尖銳的極小值與噪聲數據有關（圖2（d）），更多的學生節(jié)點能夠與教師節(jié)點相匹配。

隱式正則化

另一方面，捕捉行為強制執(zhí)行贏者通吃規(guī)則：在優(yōu)化之后，教師節(jié)點會被少數學生節(jié)點完全覆蓋（即解釋），而不是由于過度參數化而在學生節(jié)點之間分裂。這解釋了為什么同一網絡一旦經過結構化數據訓練，就可以推廣到測試集。

彩票現(xiàn)象

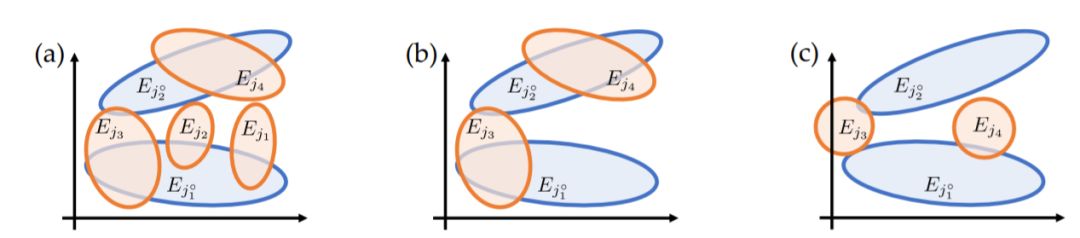
圖3

如果我們將“顯著權重”（大幅度訓練的權重）重置為優(yōu)化前的值，但在初始化之后，對其他權重進行壓縮（比例通常大于總權重的90％）并重新訓練模型，結果性能相當或更好。如果我們重新初始化顯著權重，測試性能會更差。在我們的理論中，顯著權重是一些幸運區(qū)域（圖3中的Ej3和Ej4），它們在初始化后恰好與一些教師節(jié)點重疊并在優(yōu)化中收斂教師節(jié)點。

因此，如果我們重置顯著權重并修剪其他權重，它們仍然可以收斂到同一組教師節(jié)點上，并且由于與其他不相關節(jié)點的干擾較少，可能實現(xiàn)更好的性能。但是，如果我們重新初始化，最終這些節(jié)點可能會落入那些不能覆蓋教師節(jié)點的不利區(qū)域，從而導致性能不佳（圖3（c）），就像參數化不足時的表現(xiàn)一樣。

實驗設置和方法

我們對全連接（FC）網絡和卷積網絡都進行了評估。對于全連接網絡，使用大小為50-75-100-125的ReLU教師網絡。對于卷積網絡，使用大小為64-64-64-64的教師網絡。學生網絡的深度與教師網絡相同，但每層的節(jié)點/通道是前者的10倍，因此它們是過度參數化的。添加BatchNorm時，會在ReLU之后添加。

本文采用兩種量度來衡量對一些幸運的學生節(jié)點收斂至教師節(jié)點情況的預測：

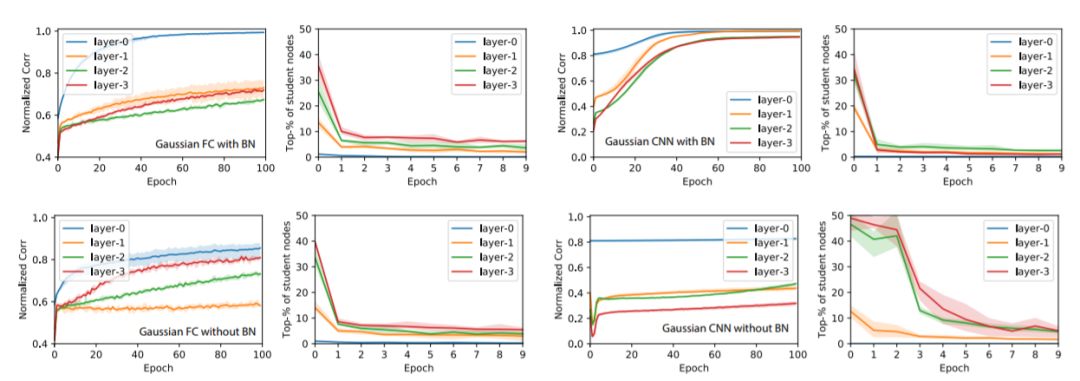
圖4：歸一化相關度ρˉ和平均排名rˉ在GAUS訓練集上隨epoch的變化

歸一化相關度ρˉ

我們計算出在驗證集上評估的教師和學生激活之間的歸一化相關度（或余弦相似度）ρ。在每一層中，我們對教師節(jié)點上的最佳相關度進行平均得到ρˉ，ρˉ≈1表示大多數教師節(jié)點至少由一名學生覆蓋。

平均排名rˉ

訓練后，每個教師節(jié)點j?都具備了相關度最高的學生節(jié)點j。這時對j的相關度等級進行檢測，并歸一化為[0,1]（0 表示排名第一），回到初始化和不同的epoch階段，并在教師節(jié)點上進行平均化，產生平均排名rˉ。rˉ值較小意味著最初與教師節(jié)點保持高相關度的學生節(jié)點一直將這一領先保持至訓練結束。

實驗結果

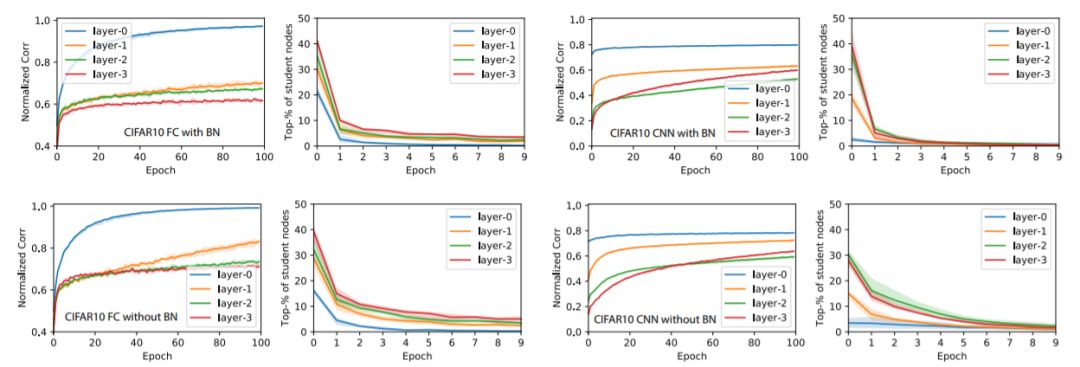
圖5：將圖4的實驗在CIFAR-10數據集上進行的結果

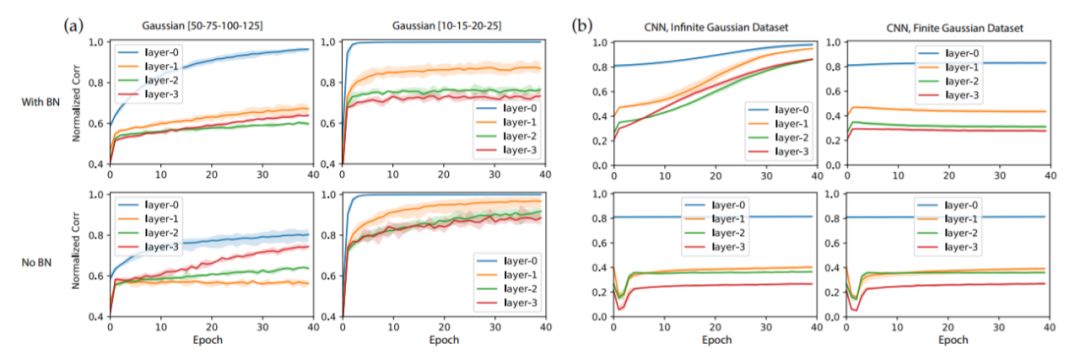
圖6：在GAUS數據集上的Ablation學習結果

關于教師網絡的大小：對于小型教師網絡（10-15-20-25，全連接網絡），收斂速度要快得多，不使用BatchNorm的訓練比使用BatchNorm訓練要快。 對于大型教師網絡，BatchNorm肯定會提高收斂速度和ρˉ的增長。

關于有限與無限數據集：我們還在卷積神經網絡的案例中使用預生成的GAUS有限數據集重復實驗，并發(fā)現(xiàn)節(jié)點相似性的收斂在幾次迭代后終止。這是因為一些節(jié)點在其激活區(qū)域中接收的數據點非常少，這對于無限數據集來說不是問題。我們懷疑這可能是CIFAR-10作為有限數據集沒有表現(xiàn)出GAUS類似行為的原因。