深度學習的一個顯著成功應用是嵌入，這是一種將離散變量表示為連續向量的方法。這項技術已經有了實際的應用，其中有在機器翻譯中使用詞嵌入和類別變量中使用實體嵌入。

近年來，神經網絡在圖像分割、自然語言處理、時間序列預測等方面的應用有了很大的發展。深度學習的一個顯著成功應用是嵌入，這是一種將離散變量表示為連續向量的方法。這項技術已經有了實際的應用，其中有在機器翻譯中使用詞嵌入和類別變量中使用實體嵌。

在本文中，我將解釋什么是神經網絡嵌入，為什么要使用它們，以及如何學習它們。我們會在真正的問題的上下文中討論這些概念：將Wikipedia上的所有圖書表示為向量，并創建圖書推薦系統。

Wikipedia上所有書的神經網絡嵌入

嵌入

嵌入是一個從離散變量到連續數字向量的映射。在神經網絡的上下文中，embeddings是低維的， 離散變量用學習到的連續向量表示。神經網絡嵌入是有用的，因為它們可以減少類別變量的維數，并有意義地在轉換空間中表示類別。

神經網絡嵌入有3個主要目的：

① 在嵌入空間中查找最近的鄰居。這些鄰居可以用于根據用戶興趣或聚類類別提出建議。

② 作為監督任務的機器學習模型的輸入。

③ 用于概念的可視化和類別之間的關系的可視化。

這意味著在圖書項目中，使用神經網絡嵌入，我們可以把維基百科上所有的37000篇圖書文章，用一個具有50個數字的向量來表示每一篇文章。此外，由于嵌入式是學習的，在我們的學習問題上下文中更相似的書籍在嵌入式空間中更接近。

神經網絡嵌入克服了用獨熱編碼表示分類變量的兩個局限性：

獨熱編碼的局限性

獨熱編碼類別變量的操作實際上是一個簡單的嵌入，其中每個類別都映射到一個不同的向量。這個過程采用離散實體，并將每個觀察結果映射到一個只有一個1的向量中。

獨熱編碼技術有兩個主要缺點：

① 對于高基數變量—那些具有許多類別的變量—轉換之后向量的維數變得太大了。

② 這種映射是完全沒有監督的：“相似”的類別在嵌入空間中并沒有彼此放置得更靠近。

第一個問題很好理解：對于每個額外的類別(稱為實體)，我們必須向一個熱編碼向量添加另一個數字。如果我們在Wikipedia上有37000本書，那么表示這些書需要為每本書提供37000維的向量，這使得針對這種表示的任何機器學習模型的訓練都是不可行的。

第二個問題同樣是有局限的：獨熱編碼不會將相似的實體彼此靠近的放在向量空間中。如果我們使用余弦距離來度量向量之間的相似性，那么經過獨熱編碼后，實體之間的相似性為0。

這意味著，《戰爭與和平》和《安娜?卡列尼娜》(這兩本書都是列夫?托爾斯泰(Leo Tolstoy)的經典著作)這樣的實體彼此之間的距離，并不比《戰爭與和平》與《銀河系漫游指南》之間的距離更近。

# One Hot Encoding Categoricals

books = ["War and Peace", "Anna Karenina",

"The Hitchhiker's Guide to the Galaxy"]

books_encoded = [[1, 0, 0],

[0, 1, 0],

[0, 0, 1]]

Similarity (dot product) between First and Second = 0

Similarity (dot product) between Second and Third = 0

Similarity (dot product) between First and Third = 0

考慮到這兩個問題，表示類別變量的理想解決方案是需要更少的數字，而不是類別的數量，并且將類似的類別放在更靠近的位置。

# Idealized Representation of Embedding

books = ["War and Peace", "Anna Karenina",

"The Hitchhiker's Guide to the Galaxy"]

books_encoded_ideal = [[0.53, 0.85],

[0.60, 0.80],

[-0.78, -0.62]]

Similarity (dot product) between First and Second = 0.99

Similarity (dot product) between Second and Third = -0.94

Similarity (dot product) between First and Third = -0.97

為了更好地表示類別實體，我們可以使用嵌入神經網絡和監督任務來學習嵌入。

學習嵌入

使用one-hot編碼的主要問題是轉換不依賴于任何監督。我們可以通過在有監督的任務中使用神經網絡來學習嵌入，從而大大改進嵌入。嵌入形成參數—網絡的權重—經過調整以最小化任務上的損失。得到的嵌入向量表示類別，其中相似的類別(相對于任務)彼此更接近。

例如，如果我們有一個包含50,000個單詞的電影評論集合，我們可以使用一個訓練好的嵌入式神經網絡來預測評論是的情感，從而為每個單詞學習100維的嵌入。詞匯表中與正面評價相關的單詞，如“brilliant”或“excellent”，將在嵌入空間中出現得更近，因為網絡已經了解到它們都與正面評價相關。

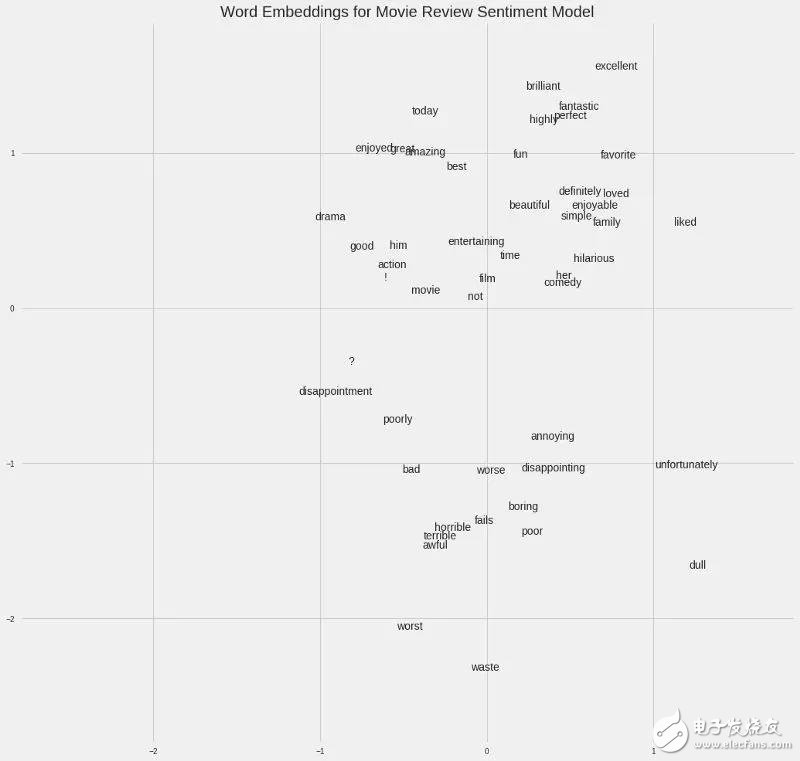
電影句子中的詞嵌入

在上面給出的書的例子中，我們的監督任務可以是“確定一本書是否是列夫·托爾斯泰寫的”，由此產生的嵌入將使托爾斯泰寫的書彼此更接近。解決如何創建監督任務來生成相關表示的問題是嵌入過程中最困難的部分。

實現

在Wikipedia book項目中，監督學習任務被設置為預測一本書的文章中是否出現了指向Wikipedia頁面的給定鏈接。我們提供成對的(書名、鏈接)訓練示例，其中混合了正樣本對和負樣本對。這種設置基于這樣的假設，即鏈接到類似Wikipedia頁面的書籍彼此相似。因此，由此產生的嵌入應該將類似的書籍更緊密地放置在向量空間中。

我使用的網絡有兩個平行的嵌入層，分別映射書和wikilink，用來區分50維向量，還有一個點積層，將嵌入的內容組合成一個數字，用于預測。嵌入是網絡的參數或權重，在訓練過程中進行調整，以最小化監督任務的損失。

在Keras代碼中，這看起來像這樣(如果你不完全理解代碼，不要擔心，直接跳到圖像)：

# Both inputs are 1-dimensional

book = Input(name = 'book', shape = [1])

link = Input(name = 'link', shape = [1])

# Embedding the book (shape will be (None, 1, 50))

book_embedding = Embedding(name = 'book_embedding',

input_dim = len(book_index),

output_dim = embedding_size)(book)

# Embedding the link (shape will be (None, 1, 50))

link_embedding = Embedding(name = 'link_embedding',

input_dim = len(link_index),

output_dim = embedding_size)(link)

# Merge the layers with a dot product along the second axis (shape will be (None, 1, 1))

merged = Dot(name = 'dot_product', normalize = True, axes = 2)([book_embedding, link_embedding])

# Reshape to be a single number (shape will be (None, 1))

merged = Reshape(target_shape = [1])(merged)

# Output neuron

out = Dense(1, activation = 'sigmoid')(merged)

model = Model(inputs = [book, link], outputs = out)

# Minimize binary cross entropy

model.compile(optimizer = 'Adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

雖然在有監督的機器學習任務中，目標通常是訓練一個模型對新數據進行預測，但在這個嵌入模型中，預測只是達到目的的一種手段。我們想要的是嵌入權值，將書籍和鏈接表示為連續向量。

嵌入本身并不那么有趣，它們只是數字的向量：

來自書籍推薦嵌入模型的示例嵌入

然而，嵌入可以用于前面列出的3個目的，對于這個項目，我們主要感興趣的是推薦基于最近鄰的書籍。為了計算相似性，我們取一本書進行查詢，找到它的向量與其他所有圖書向量的點積。(如果我們的嵌入是標準化的，那么這個點積就是向量之間的cos距離，范圍從-1(最不相似)到+1(最相似)。我們也可以用歐氏距離來度量相似性。

這是我建立的圖書嵌入模型的輸出：

Books closest to War and Peace.

Book: War and Peace Similarity: 1.0

Book: Anna Karenina Similarity: 0.79

Book: The Master and Margarita Similarity: 0.77

Book: Doctor Zhivago (novel) Similarity: 0.76

Book: Dead Souls Similarity: 0.75

(向量與自身的余弦相似度必須為1.0)。經過降維(見下圖)，可以得到如下圖：

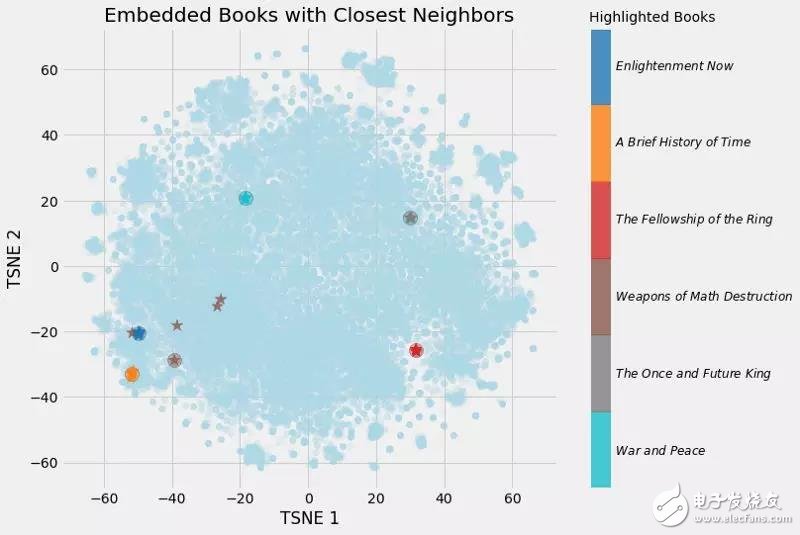
書的嵌入以及最近的鄰居

我們可以清楚地看到學習嵌入的價值！現在，維基百科上每一本書都有一個50個數字的向量表示，相似的書彼此之間距離更近。

嵌入可視化

嵌入的最酷的部分之一是，它們可以用來可視化概念，例如“小說”或“非小說”之間的關系。這需要進一步的降維技術來將維度降為2或3。最常用的約簡方法本身就是一種嵌入方法：t分布隨機鄰接嵌入(TSNE)。

我們可以把維基百科上所有書籍的37000個原始維度，用神經網絡嵌入將它們映射到50個維度，然后用TSNE將它們映射到2個維度。結果如下：

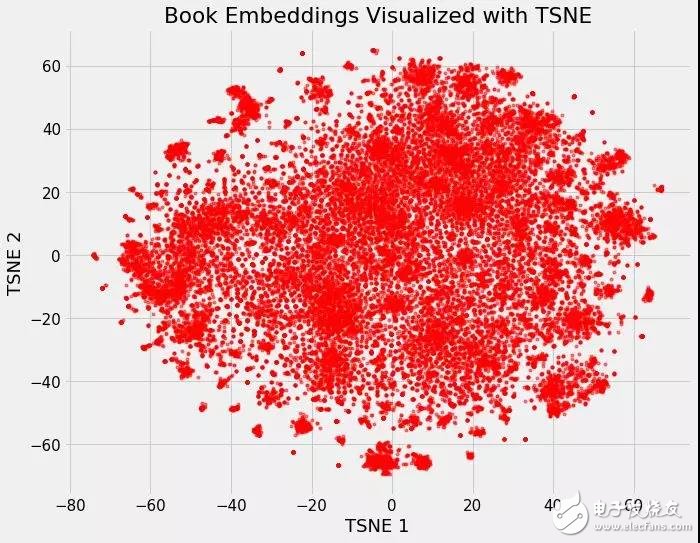
在Wikipedia上的所有37000本書的嵌入

(TSNE是一種流形學習技術，這意味著它試圖將高維數據映射到低維流形，創建一個試圖維護數據內部局部結構的嵌入。它幾乎只用于可視化，因為輸出是隨機的，不支持轉換新數據。一個正在興起的替代方案是統一流形近似和投影，UMAP，它更快，并且支持將新數據轉換到嵌入空間中)。

這本身并不是很有用，但是一旦我們開始根據不同的書的特點給它上色，它就會變得很有洞察力。

用流派對嵌入上色

我們可以清楚地看到屬于同一類型的書籍的分組。這并不完美，但仍然令人印象深刻的是，我們可以用兩個數字來表示維基百科上的所有書籍，這兩個數字仍然能夠捕捉到不同類型之間的差異。

書的例子(即將發表的完整文章)展示了神經網絡嵌入的價值：我們有一個類別對象的向量表示，它是低維的，并且在嵌入空間中將相似的實體彼此放置得更近。

交互式可視化

靜態圖的問題是，我們不能真正地研究數據并研究變量之間的分組或關系。為了解決這個問題，TensorFlow開發了projector，這是一個在線應用程序，可以讓我們可視化并與嵌入進行交互。我將很快發布一篇關于如何使用這個工具的文章，但是現在，結果如下：

使用projector交互式探索書籍嵌入

結論

神經網絡嵌入是學習離散數據作為連續向量的低維表示。這些嵌入克服了傳統編碼方法的限制，可以用于查找最近的鄰居、輸入到另一個模型和可視化。

雖然很多深度學習的概念都是在學術術語中討論的，但是神經網絡嵌入既直觀又相對容易實現。我堅信任何人都可以學習深度學習并使用Keras這樣的庫構建深度學習解決方案。嵌入是處理離散變量的有效工具，是深度學習的一個有用應用。